
|
Рефератыкосмонавтике административному праву хозяйственному праву устройствам экологическому праву криминалогия гражданский и землепользование обществознание |
Дипломная работа: Комплексные числа (избранные задачи)Решение Так как Ответ: Задача 53. Изобразите на
комплексной плоскости множество точек, удовлетворяющих условию Решение Пусть
Искомое множество
изображено на рис. 28. Отметим, что граница множества (прямая
Рис. 28. Задача 53. Множество
точек комплексной плоскости определяется условие Решение Множество точек, заданное
условием Пусть
имеет хотя бы одно решение? Последняя система равносильна следующей:
Эта система имеет решения
тогда, когда имеет решение квадратное неравенство
Ответ: 2.3. Тригонометрическая форма комплексных чисел Пусть вектор Обозначим
через φ угол между положительной полуосью Ox и вектором
Рис. 29 Обозначим
длину вектора
Тогда
Запись отличного от нуля комплексного числа z в виде
называется тригонометрической формой комплексного числа z. Число r называется модулем комплексного числа z, а число φ называется аргументом этого комплексного числа и обозначается Arg z. Тригонометрическая форма записи комплексного числа – (формула Эйлера) – показательная форма записи комплексного числа:
У комплексного числа z имеется бесконечно много аргументов: если φ0 – какой-либо аргумент числа z, то все остальные можно найти по формуле
Для
комплексного числа Таким
образом, аргументом отличного от нуля комплексного числа
Значение
φ аргумента комплексного числа z, удовлетворяющее неравенствам Аргументы Arg z и arg z связаны равенством
где Формула Главное
значение аргумента отличного от нуля комплексного числа
Формулы умножения и деления комплексных чисел в тригонометрической форме имеют следующий вид:
При возведении в натуральную степень комплексного числа используется формула Муавра:
При извлечении корня из комплексного числа используется формула:
где k=0, 1, 2, …, n-1. Задача 54. Вычислите Решение Представим
решение данного выражения в показательной форме записи комплексного числа: Если Тогда Ответ: Задача 55. Запишите комплексные числа в тригонометрической форме: а) Решение Так как
тригонометрическая форма комплексного числа имеет вид а) В комплексном числе Тогда
Поэтому б) в) г) д) е) ж) Поэтому Ответ: Задача 56. Найдите тригонометрическую форму комплексного числа
Решение Пусть Тогда Поскольку
Следовательно,
Ответ: Задача 57. Используя
тригонометрическую форму комплексного числа, произведите указанные действия: Решение. Представим числа 1) Находим значение главного
аргумента
Подставим значения 2)
3) Найдем частное
Далее, применяя формулу (9) получим:
Полагая k=0, 1, 2, получим три различных значения искомого корня: Если если если Ответ:
Задача 58. Пусть а) число б) имеет место равенство:
Решение а) Представим данные комплексные числа в тригонометрической форме:
Предположим, что
Последнее выражение
является положительным числом, так как под знаками синусов стоят числа из
интервала б) Имеем
так как число Кроме того,
Задача 59. Запишите в
алгебраической форме число Решение Представим число
Отсюда следует равенство:
Применяя формулу Муавра: получаем
Найдена тригонометрическая форма заданного числа. Запишем теперь это число в алгебраической форме:
Ответ: Задача 60. Найдите сумму
Решение Рассмотрим сумму
Применяя формулу Муавра, найдем
Эта сумма представляет
собой сумму n членов геометрической прогрессии со
знаменателем Применяя формулу для суммы членов такой прогрессии, имеем
Выделяя мнимую часть в
последнем выражении, находим
Итак, Выделяя действительную
часть, получаем также следующую формулу: Ответ: Задача 61. Найдите сумму: а) Решение По формуле Ньютона для возведения в степень имеем
По формуле Муавра находим:
Приравнивая вещественные
и мнимые части полученных выражений для
Эти формулы в компактном виде можно записать так:
Ответ: Задача 62. Найдите все Решение Поскольку
Следовательно,
Точки,
соответствующие числам
Рис. 30. Ответ:
Задача
63. Решите уравнение Решение По
условию Для того
чтобы число z было корнем данного уравнения, нужно,
чтобы число Отсюда
заключаем, что исходное уравнение имеет
Таким образом,
т. е. Ответ: Задача 64. Решите во
множестве комплексных чисел уравнение Решение Так как число
Все корни этого уравнения получаются из формулы (см. задачу 62):
Ответ:
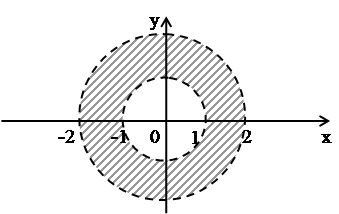
Задача 65. Изобразите на
комплексной плоскости множество точек, удовлетворяющих неравенствам: Решение Пусть Тогда Комплексным числам,
имеющим одинаковые модули, соответствуют точки плоскости, лежащие на окружности
с центром в начале координат, поэтому неравенству
Рис. 31.
Рис. 32. Преобразование Предложенный способ, использующий идею геометрических преобразований плоскости, наверное, менее удобен в описании, но весьма изящен и эффективен. Задача 66. Найдите Решение Пусть Запишем число z в тригонометрической форме:
Ответ: – 64. Задача 67. Для
комплексного числа Решение Представим число В первом случае
Ответ: Задача 68. Найдите сумму
таких чисел Решение Заметим, что уже из самой
формулировки задачи можно понять, что сумма корней уравнения можно найти без
вычисления самих корней. Действительно, сумма корней уравнения Приведем и другое
возможное обоснование. Пусть Допустимо и такое решение. Представив правую часть исходного уравнения в тригонометрической форме, получим
Далее вычисляем сумму четырех корней, которая равна нулю. Ответ: 2.4. Приложение теории комплексных чисел к решению уравнений 3- и 4-й степени Рассмотрим решение кубического уравнения
на конкретном примере. Пример 1. Решите уравнение
Решение. Приведем сначала наше уравнение к уравнению, не содержащему квадрат неизвестной (такое уравнение называется приведенным), т.е. к уравнению вида:
для чего произведем подстановку:
Получим уравнение:
Раскрыв скобки и приведя подобные члены, приходим к уравнению:
где (Замечание. Переход к приведенному кубическому уравнению можно
осуществить с помощью схемы Горнера, разложив многочлен Для корней кубического уравнения
имеется так называемая формула Кардано, хотя правильнее было бы ее называть формулой дель Ферро – Тартальи - Кардано. Впервые приведенное кубическое уравнение
решил профессор Болонского университета Сципион дель Ферро в конце XV века. Затем в 1535 году те же формулы были выведены Николо Тартальей. Наконец, в 1545 году решение уравнения (1) было изложено в книге Джероламо Кардано "Ars Magna" ("Великое искусство"). Формулы Кардано имеют вид:
где
Практически корни Пусть
где e1 и e2 – значения корня кубического из 1 , т.е.
Если вычислить
Действительно,
Аналогично доказывается равенство Подставляя полученные значения
находим практические формулы:
В нашем случае:
Таким образом, положим
следовательно,
Из последних равенств, учитывая, что
Ответ: Для приведенного кубического уравнения
дискриминант вычисляется по формуле:
При этом: а) если б) если в) если Таким образом, в любом случае уравнение (3) с действительными коэффициентами имеет хотя бы один действительный корень. Рассмотрим решение уравнения 4-й степени методом Феррари на конкретном примере. Пример 2. Решите уравнение
Решение. Оставим в левой части уравнения члены, содержащие
Дополним левую часть полученного уравнения до полного квадрата:
или
Введем в полный квадрат левой части равенства (1) параметр r:
Откуда с учетом равенства (1) получим:
Подберем значение параметра r таким образом, чтобы дискриминант правой части равенства (2) обратился в нуль (т.е. чтобы в правой части равенства (2) также получился полный квадрат).
Дискриминант D равен нулю тогда и только тогда, когда число r является корнем уравнения:
В частности, Подставив значение
или
Откуда,
Следовательно,
Ответ:
Задача 69. Решите уравнение Решение Данное уравнение – приведенное. Здесь
Для извлечения кубического корня из комплексного числа представим его в тригонометрической форме:
поэтому При
Значит,
поэтому Следовательно,
Ответ: 2; Задача 70. Решите уравнение |
|
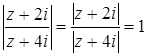 , то
, то 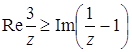 .
.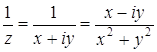 и, значит,
и, значит, 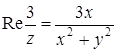 ,
, 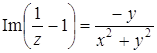 .
Исходное неравенство перепишется так:
.
Исходное неравенство перепишется так: 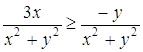 . Последнее неравенство можно заменить системой двух
условий:
. Последнее неравенство можно заменить системой двух
условий: 
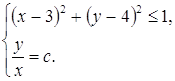
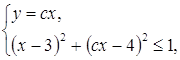 или
или 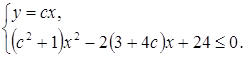
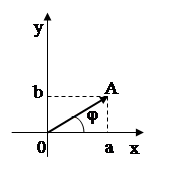
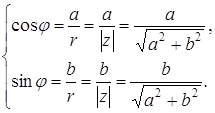 (3)
(3)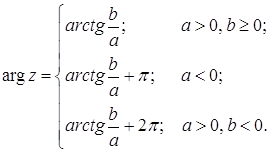
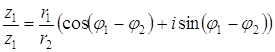 . (7)
. (7)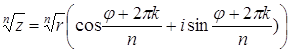 , (9)
, (9)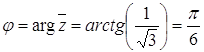 . Поэтому
. Поэтому 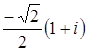 .
.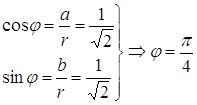 ,
,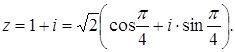
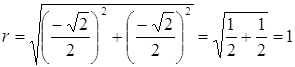 , а
, а 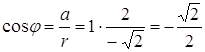 , то
, то 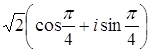 ;
; 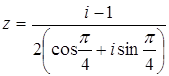 .
.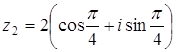 .
.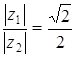 , а
, а 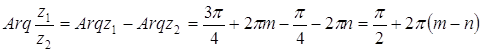 .
.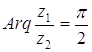 , поэтому
, поэтому 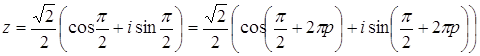 , где
, где 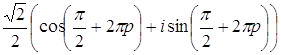 , где
, где 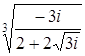 .
.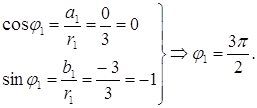
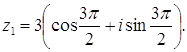
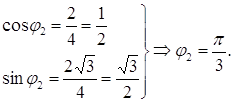 Тогда
Тогда 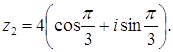
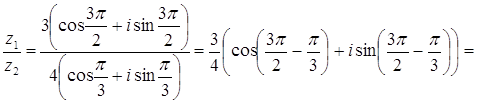
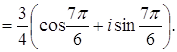
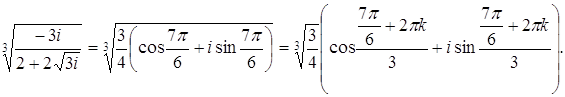
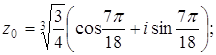
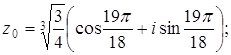
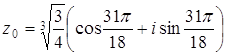 .
.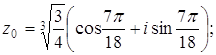
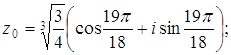
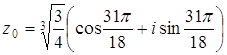 .
.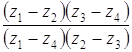 является действительным положительным числом;
является действительным положительным числом;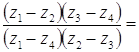
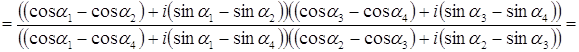
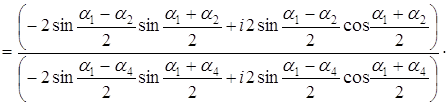
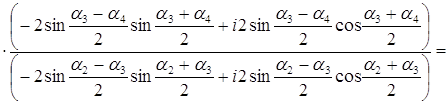
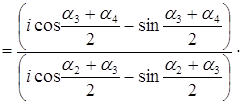
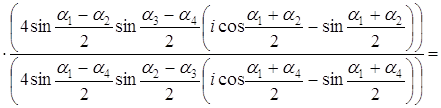
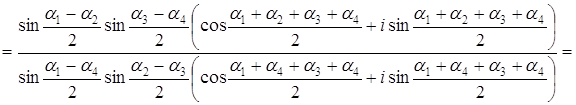
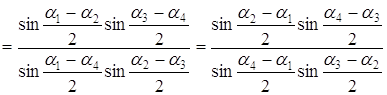 .
.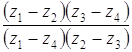 вещественно и положительно.
Действительно, если a и b – комплексные числа и
вещественно и положительно.
Действительно, если a и b – комплексные числа и 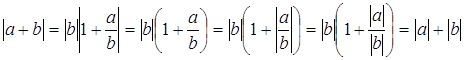 .
.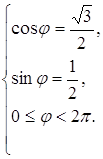
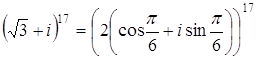 .
.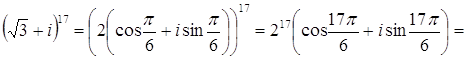
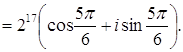
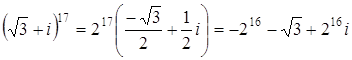 .
.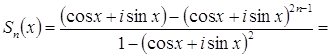
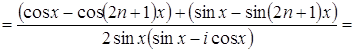
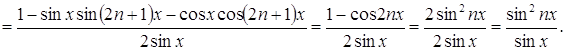
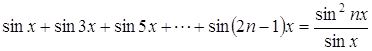 .
.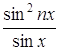 .
.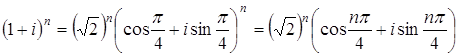 .
.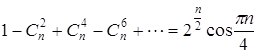 и
и 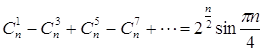 .
.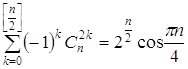 ,
,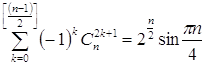 , где
, где 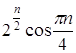 ;
; 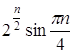 .
.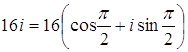 , то, применяя формулу
, то, применяя формулу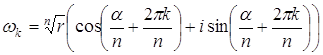 ,
, 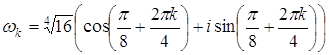 ,
, 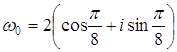 ,
, 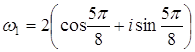 ,
, 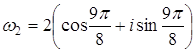 ,
, 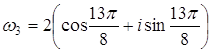 .
.
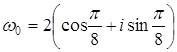 ,
, 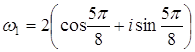 ,
,
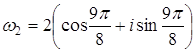 ,
, 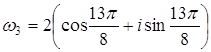 .
.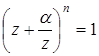 .
.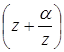 было корнем п-й
степени из числа 1.
было корнем п-й
степени из числа 1.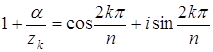 ,
, 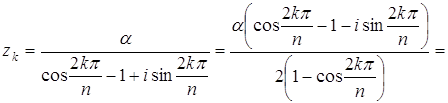
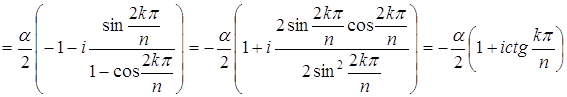 ,
,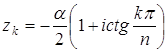 ,
, 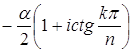 .
.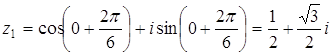 ,
,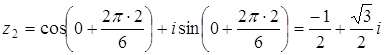 ,
,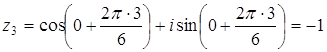 ,
,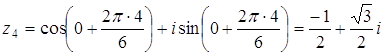 ,
, .
.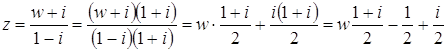 .
.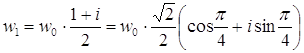 , имеет модуль, в
, имеет модуль, в 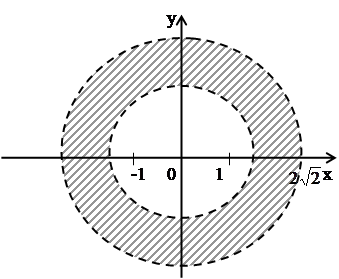
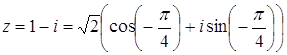 , где
, где 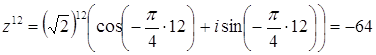 .
.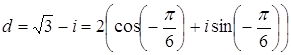 . Отсюда
. Отсюда 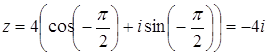 , во втором
, во втором 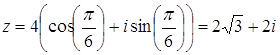 .
.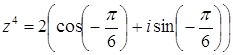 . Отсюда
. Отсюда 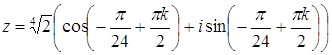 , где
, где 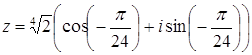 –
одно из таких чисел.
–
одно из таких чисел.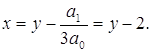
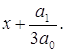 )
) 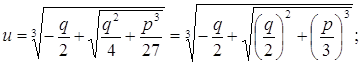
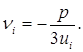
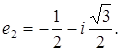
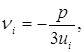 то получим:
то получим: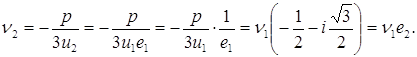
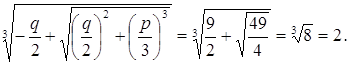
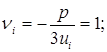
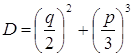 .
.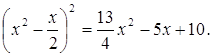 (1)
(1)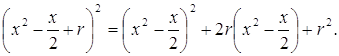
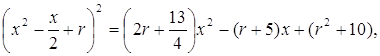 (2)
(2)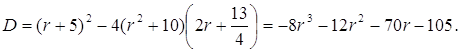
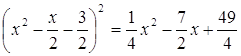 ,
,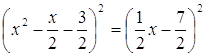 .
.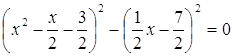 ,
,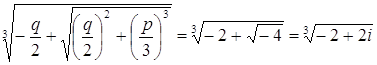 .
.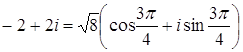 ,
,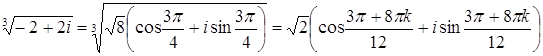 ,
где
,
где 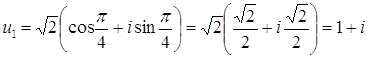 .
.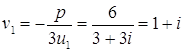 ,
,