
|
Рефератыкосмонавтике административному праву хозяйственному праву устройствам экологическому праву криминалогия гражданский и землепользование обществознание |
Дипломная работа: Комплексные числа (избранные задачи)Дипломная работа: Комплексные числа (избранные задачи)ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ» КАФЕДРА АГЛЕБРЫ И ГЕОМЕТРИИ Комплексные числа (избранные задачи) ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА по специальности 050201.65 математика (с дополнительной специальностью 050202.65 информатика) Выполнила: студентка 5 курса физико-математического факультета Научный руководитель: ВОРОНЕЖ – 2008 Содержание 1. Введение……………………………………………………...…………..… 2. Комплексные числа (избранные задачи) 2.1. Комплексные числа в алгебраической форме….……...……….…. 2.2. Геометрическая интерпретация комплексных чисел…………..… 2.3. Тригонометрическая форма комплексных чисел 2.4. Приложение теории комплексных чисел к решению уравнений 3-й и 4-й степени……………..……………………………………………………… 2.5. Комплексные числа и параметры………...……………………...…. 3. Заключение……………………………………………………................. 4. Список литературы………………………….…………………............... 1. Введение В программе математики школьного курса теория чисел вводится на примерах множеств натуральных чисел, целых, рациональных, иррациональных, т.е. на множестве действительных чисел, изображения которых заполняют всю числовую ось. Но уже в 8 классе запаса действительных чисел не хватает, решая квадратные уравнения при отрицательном дискриминанте. Поэтому было необходимо пополнить запас действительных чисел при помощи комплексных чисел, для которых квадратный корень из отрицательного числа имеет смысл. Выбор темы «Комплексные числа», как темы моей выпускной квалификационной работы, заключается в том, что понятие комплексного числа расширяет знания учащихся о числовых системах, о решении широкого класса задач как алгебраического, так и геометрического содержания, о решении алгебраических уравнений любой степени и о решение задач с параметрами. В данной дипломной работе рассмотрено решение 82-х задач. В первой части основного раздела «Комплексные числа» приведены решения задач с комплексными числами в алгебраической форме, определяются операции сложения, вычитания, умножения, деления, операция сопряжения для комплексных чисел в алгебраической форме, степень мнимой единицы, модуль комплексного числа, а также излагается правило извлечения квадратного корня из комплексного числа. Во второй части решаются задачи на геометрическую интерпретацию комплексных чисел в виде точек или векторов комплексной плоскости. В третьей части рассмотрены действия над комплексными числами в тригонометрической форме. Используются формулы: Муавра и извлечение корня из комплексного числа. Четвертая часть посвящена решению уравнений 3-й и 4-й степеней. При решении задач последней части «Комплексные числа и параметры» используются и закрепляются сведения, приведенные в предыдущих частях. Серия задач главы посвящена определению семейств линий в комплексной плоскости, заданных уравнениями (неравенствами) с параметром. В части упражнений нужно решить уравнения с параметром (над полем С). Есть задания, где комплексная переменная удовлетворяет одновременно ряду условий. Особенностью решения задач этого раздела является сведение многих из них к решению уравнений (неравенств, систем) второй степени, иррациональных, тригонометрических с параметром. Особенностью изложения материала каждой части является первоначальный ввод теоретических основ, а в последствии практическое их применение при решении задач. В конце дипломной работы представлен список используемой литературы. В большинстве из них достаточно подробно и доступно изложен теоретический материал, рассмотрены решения некоторых задач и даны практические задания для самостоятельного решения. Особое внимание хочется обратить на такие источники, как: 1. Гордиенко Н.А., Беляева Э.С., Фирстов В.Е., Серебрякова И.В. Комплексные числа и их приложения: Учебное пособие. [10]. Материал учебного пособия изложен в виде лекционных и практических занятий. 2. Шклярский Д.О., Ченцов Н.Н., Яглом И.М. Избранные задачи и теоремы элементарной математики. Арифметика и алгебра. [21] Книга содержит 320 задач, относящихся к алгебре, арифметике и теории чисел. По своему характеру эти задачи значительно отличаются от стандартных школьных задач. 2. Комплексные числа (избранные задачи) 2.1. Комплексные числа в алгебраической форме Решение многих задач математики, физики сводится к решению алгебраических уравнений, т.е. уравнений вида
где a0 , a1 , …, an действительные числа. Поэтому исследование алгебраических уравнений является одним из важнейших вопросов в математике. Например, действительных корней не имеет квадратное уравнение с отрицательным дискриминантом. Простейшим таким уравнением является уравнение
Для того чтобы это уравнение имело решение, необходимо расширить множество действительных чисел путем присоединения к нему корня уравнения
Обозначим
этот корень через
следовательно,
Символ
Полученное выражение назвали комплексными числами, поскольку они содержали как действительную, так и мнимую части. Итак, комплексными числами называются выражения вида
где
Комплексные
числа вида Комплексные
числа вида
Алгебраическая запись комплексных чисел позволяет производить операции над ними по обычным правилам алгебры. Суммой двух комплексных чисел
Произведением двух комплексных чисел
1. Коммутативный (переместительный) закон сложения:
2. Ассоциативный (сочетательный) закон сложения:
3. Коммутативный закон умножения:
4. Ассоциативный закон умножения:
5. Дистрибутивный (распределительный) закон умножения относительно сложения:
6. 7. 8. 9. Любому
комплексному числу 10. Всякому
комплексному числу Степени мнимой единицы.
Если
натуральный показатель степени m при
делении на 4 дает в остатке r,
т.е. если
при этом Комплексное
число
Свойства операции сопряжения. 1.
2.
Для любого
действительного числа a
справедливо равенство 3.
Для любого
действительного числа b
справедливо равенство 4.
5.
Следствие из
5. 6.
7. Сумма и произведение двух комплексно сопряженных чисел являются действительными числами.
Следствие из
7. Модулем
комплексного числа
8. Теорема о сопряженном корне. Если число
с
действительным коэффициентами a0 , a1 , …, an , то число Извлечение
квадратного корня из комплексного числа
где x и y – действительные числа. Возводя обе части этого равенства в квадрат, получаем
Что равносильно системе
Решая эту систему, получаем:
Таким образом, извлечение корня квадратного из комплексного числа осуществляется по формуле
В скобках
перед мнимой единицей берется знак плюс, если Задача 1.
Найдите комплексные корни уравнения а) Решение а) Так как б) Учитывая, что
в) Преобразуем Ответ: а) Задача 2. Найдите x и y, для которых Решение Получим и решим систему двух уравнений:
Ответ: Задача 3. Решите
уравнение Решение Левую часть уравнения
можно рассматривать, как некоторое неизвестное комплексное число. Приведя его к
виду
Ответ: Задача 4. При каких
действительных значениях x и y комплексные числа Решение Комплексные числа Ответ: Задача 5. При каких
действительных значениях x и y комплексные числа Решение Комплексные числа
Ответ: Задача 6. Решите
уравнение Решение Левую часть уравнения
можно рассматривать, как некоторое неизвестное комплексное число. Приведя его к
виду
Ответ: Задача 7. Решите во
множестве комплексных чисел уравнение Решение Так как Отсюда, Ответ: Задача 8. Решите
уравнение Решение Перепишем уравнение в
виде Полагая Для нахождения коэффициентов квадратного трехчлена применим схему Горнера:
Итак, получаем уравнение Квадратный трехчлен Следовательно, исходное
уравнение имеет корни: Ответ: Задача 9. Решите
уравнение Решение Корни данного уравнения находятся по формулам
где
Находим два решения этой
системы: решениями исходного
уравнения являются числа
Ответ: Задача 10. Произведите действия с комплексными числами в алгебраической форме: а) Решение а) б) в)
Ответ: а) Задача 11. Произведите следующие действия над комплексными числами: а) Решение а) б) в) г) Ответ: а) Задача 12. Запишите
комплексное число Решение Имеем
Ответ: Задача 13. Найдите
значение функции Решение Подставим значение x в функцию:
Вычислим второе слагаемое:
Вычислим первое слагаемое:
Таким образом, Ответ: Задача 14. Вычислите Решение С помощью формулы: Легко получаем:
Ответ: Задача 15. Выполните
указанные действия: Решение Вычислим значение дроби Следовательно, Ответ: Задача 16.
Решите уравнение Решение По формуле Заметим, что
найденные в этой задаче корни являются сопряженными: Ответ: Задача 17.
Составьте приведенное квадратное уравнение с действительными коэффициентами,
имеющий корень Решение Второй корень
где число 2 – это второй коэффициент уравнения, взятый с противоположным знаком, а число 5 – свободный член. Таким образом, получаем уравнение Ответ: Задача 18.
Даны числа а) Решение а)
б)
Задача 19. Зная, что
корнем уравнения Решение Поскольку все
коэффициенты данного уравнения – действительные числа, то на основании теоремы
о сопряженном корне, делаем вывод, что число Пусть
Разделим обе части
последнего равенства на Следовательно, Ответ: Задача 20. Найдите все комплексные числа, каждое из которых сопряжено со своим квадратом. Решение Пусть По условию задачи имеем: Преобразовав это
уравнение, получим: Два комплексных числа равны тогда и только тогда, когда равны соответственно их действительные и мнимые части. Следовательно, последнее уравнение равносильно следующей системе уравнений с действительными переменными x и y:
Возможны два случая: 1) имеет следующие решения: 2) Итак, искомых чисел
четыре: Ответ: Задача 21. Известно, что а) Решение а) б) Ответ: а) Задача 22. При каких
действительных значениях x и y комплексные числа Решение Комплексные числа плексно сопряженными, если выполняются условия:
Ответ: Задача 23. Докажите
тождество Решение Пусть Отсюда легко следует доказываемое тождество. Задача 24. Докажите, что
если число Решение По условию Тождество доказано. Задача 25. Пусть Решение Поскольку
Тождество доказано. Задача 26. Решите уравнение
Решение Пусть
Из второго уравнения этой
системы находим: x=0 и y=0. При x=0 первое уравнение системы запишется в виде При y=0 для нахождения x получаем уравнение Ответ: Задача 27. Решить систему уравнений:
Решение Полагая
следовательно, После преобразований данная система принимает вид
Решение полученной
системы является пары Ответ: Задача 28. Докажите, что
если |
|
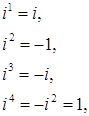
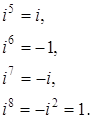
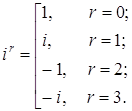
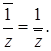
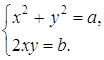
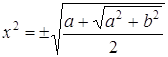 ;
; 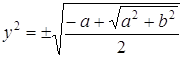 .
.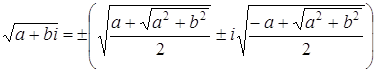 .
.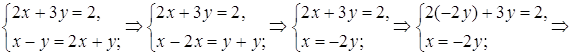
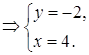
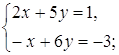
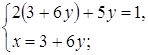
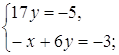
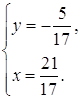
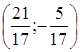 .
.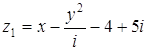 и
и 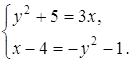
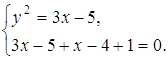
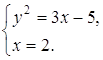
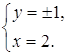
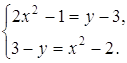
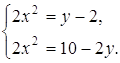
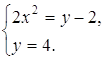
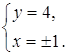
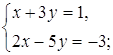
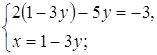
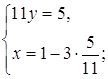
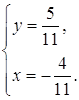
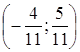 .
.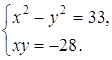
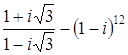 ; в)
; в) 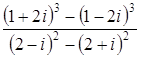 .
.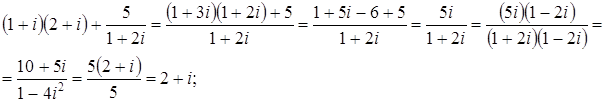
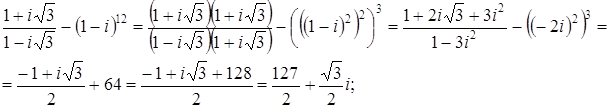
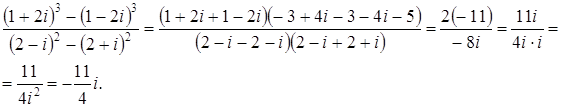
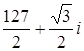 ; в)
; в) 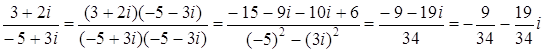 .
.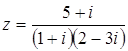 в виде
в виде 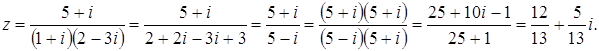
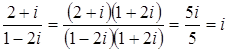 .
.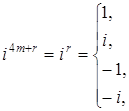
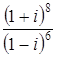 .
.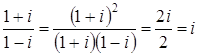 .
.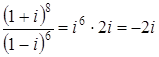
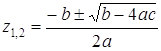 , находим:
, находим: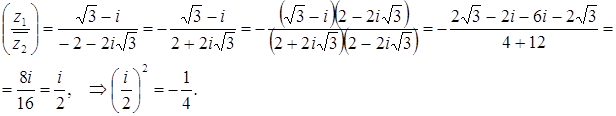 Ответ: а)
Ответ: а) 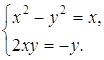
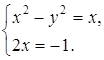 , которая
, которая 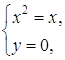 , которая имеет два решения:
, которая имеет два решения: 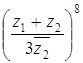 .
.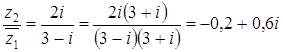 ,
,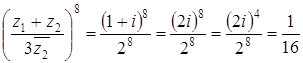 .
.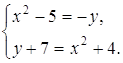
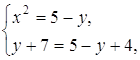
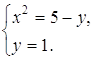
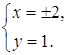
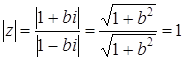 .
.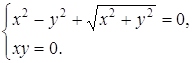
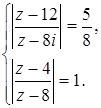
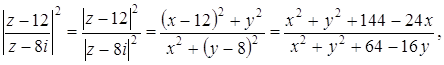
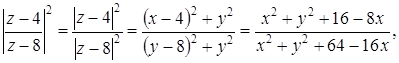
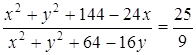 и
и 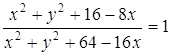 .
.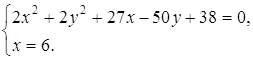
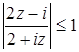 .
.