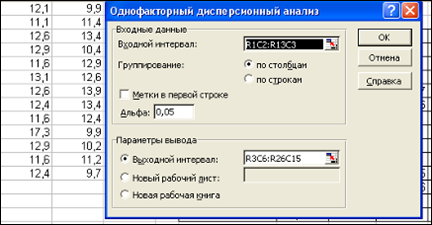
Учебное пособие: Дисперсионный анализ при помощи системы MINITAB для WINDOWS

«Входной интервал» - вводится ссылка на диапазон, содержащий анализируемые данные. Ссылка должна состоять не менее чем из двух смежных диапазонов данных, данные в которых расположены по строкам или столбцам.

«Группирование» - установите переключатель в положение. По столбцам или По строкам в зависимости от расположения данных во входном диапазоне.

«Метки в первой строке/Метки в первом столбце» - если первая строка исходного диапазона содержит названия столбцов, установите переключатель в положение Метки в первой строке. Если названия строк находятся в первом столбце входного диапазона, установите переключатель в положение Метки в первом столбце. Если входной диапазон не содержит меток, то необходимые заголовки в выходном диапазоне будут созданы автоматически.

«Альфа» - введите уровень значимости, необходимый для оценки критических параметров F-статистики. Уровень альфа связан с вероятностью возникновения ошибки типа I (опровержение верной гипотезы).

«Выходной диапазон» - введите ссылку на левую верхнюю ячейку выходного диапазона. Размеры выходной области будут рассчитаны автоматически, и соответствующее сообщение появится на экране в том случае, если выходной диапазон занимает место существующих данных или его размеры превышают размеры листа.

«Новый лист» - установите переключатель, чтобы открыть новый лист в книге и вставить результаты анализа, начиная с ячейки A1. Если в этом есть необходимость, введите имя нового листа в поле, расположенном напротив соответствующего положения переключателя.

«Новая книга» - установите переключатель, чтобы открыть новую книгу и вставить результаты анализа в ячейку A1 на первом листе в этой книге.

Пример заполнения окна «Однофакторный дисперсионный анализ» представлен на рисунке 2.

Рисунок 2 – Пример заполнения окна «Однофакторный дисперсионный анализ»

Результаты расчетов однофакторного дисперсионного анализа представлены на рисунке 3.

Рисунок 3 – Результаты расчетов по однофакторному дисперсионному анализу

Интерпретация результатов:

«Группы» - данные по выработке в первую и вторую смены.

«Счет» - количество наблюдений в каждой из групп.

«Сумма» - сумма элементов каждой из групп.

«Среднее» - средняя выработка в каждой из групп.

«Дисперсия» - рассчитывается дисперсия по каждой из групп;

SS - сумма квадратов;

df - число степеней свободы;

MS – средний квадрат;

F – расчетное значение отношения Фишера;

P - уровень значимости для вычисленного F;

F критическое – табличное значение отношения Фишера.

Результаты расчетов аналогичны результатам, полученным при расчетах вручную.

Двухфакторный дисперсионный анализ в MS Exel

Используя данный предыдущего примера, предположим, что у нас есть данные о поле работников. Для проведения двухфакторного дисперсионного анализа в MS Exel необходимо представить данные в виде перекрестной классификации:

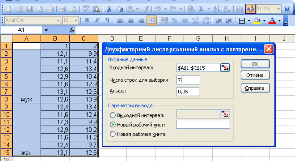
В меню «Сервис» выбрать команду «Анализ данных» и команду «Двухфакторный дисперсионный анализ с повторениями».

Далее необходимо заполнить окно «Двухфакторный дисперсионный анализ с повторениями»:

«Входной интервал» - вводится ссылка на диапазон, содержащий анализируемые данные.Необходимо отметить не только сами числа, но и заголовок таблицы.

«Число строк для выборки» - необходимо ввести количество повторений в одной ячейке. (Для нашего примера - 7)

«Альфа» - введите уровень значимости, необходимый для оценки критических параметров F-статистики. Уровень альфа связан с вероятностью возникновения ошибки типа I (опровержение верной гипотезы).

«Выходной диапазон» - введите ссылку на левую верхнюю ячейку выходного диапазона. Размеры выходной области будут рассчитаны автоматически, и соответствующее сообщение появится на экране в том случае, если выходной диапазон занимает место существующих данных или его размеры превышают размеры листа.

«Новый лист» - установите переключатель, чтобы открыть новый лист в книге и вставить результаты анализа, начиная с ячейки A1. Если в этом есть необходимость, введите имя нового листа в поле, расположенном напротив соответствующего положения переключателя.

«Новая книга» - установите переключатель, чтобы открыть новую книгу и вставить результаты анализа в ячейку A1 на первом листе в этой книге.

Пример заполнения окна «Однофакторный дисперсионный анализ» представлен на рисунке 2.

Рисунок 2 – Пример заполнения окна «Двухфакторный дисперсионный анализ»

Результаты расчетов двухфакторного дисперсионного анализа представлены на рисунке 3.

Рисунок 3 – Результаты расчетов по однофакторному дисперсионному анализу

Интерпретация результатов:

SS - сумма квадратов;

df - число степеней свободы;

MS – средний квадрат;

F – расчетное значение отношения Фишера;

P - уровень значимости для вычисленного F;

F критическое – табличное значение отношения Фишера.

4.         Задание по выполнению лабораторной работы

4.1.     Однофакторный дисперсионный анализ

Вы  собираетесь открывать магазин одежды. Произведенный опрос среди предполагаемых покупателей позволил получить вам примерный уровень доходов респондентов в месяц, которые предпочитают одежду тех или иных торговых марок.  Необходимо проверить, есть ли существенное различие в уровне доходов и маркой одежды, которую предпочитают покупатели. Выясните, какие торговые марки можно отнести к одной группе (по величине объема продаж) и предположите, как их можно сегментировать.

В табл.6 приведены варианты заданий.

Таблица 6.

4.2 Двухфакторный дисперсионный анализ

В таблице приведены данные  опроса  32  человек.  Опрашиваемые были   выбраны   случайным   образом   из  групп  людей,  которые формировались так, чтобы  результаты опроса были сбалансированы по всем уровням факторов.

Таблица 7

Результаты опроса

Требуется методом   двухфакторного   дисперсионного   анализа оценить степень  влияния  изучаемых  факторов  на  результирующий экономический показатель.   Первоначально   оценить   модель  без взаимодействия факторов,  затем   с   взаимодействием.   Сравнить результаты. Сделать выводы. Варианты заданий приведены в табл.8.

Таблица 8

Варианты заданий

5.         Порядок выполнения работы

1.         В соответствии с вариантом задания выполнить однофакторный дисперсионный анализ, сделать выводы, написать отчет.

2.         В соответствии с вариантом задания выполнить двухфакторный дисперсионный анализ, сделать выводы, написать отчет.

Контрольные вопросы

1.         Сформулируйте основную идею дисперсионного анализа, для решения каких задач он наиболее эффективен ?

2.         Что показывает F отношение Фишера?

3.         Каковы основные теоретические предпосылки дисперсионный анализ?

4.         Произведите разложение общей суммы квадратов отклонений на составляющие в однофакторном  дисперсионном анализе.

5.         Как получить оценки дисперсий из сумм квадратов отклонений?  Как получаются необходимые числа степеней свободы?

6.         Приведите свой пример двухфакторного дисперсионного анализа.

7.         На какие суммы разлагается общая сумма квадратов отклонений в двухфакторном дисперсионном анализе?

8.         Поясните схему двухфакторного  дисперсионного анализа.

9.         Чем отличается перекрестная классификация от иерархической классификации?

10.       Чем отличаются сбалансированные данные?

Литература

1.         Шеффе Г. Дисперсионный анализ. – М.: Наука. 1980.- 512с.

2.         Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и науке: Методы планирования эксперимента. Пер. с англ. – М.: Мир, 1981.-520с.

3.         Дэниел К. Применение статистики в промышленном эксперименте.-М.:Мир, 1979.-300с.

4.         Хикс Ч. Основные принципы планирования эксперимента.- М.:Мир, 1967.

Методические указания разработали: профессор, д.т.н. Цуканов А.В. и к.т.н., доцент, Русина Н.А.