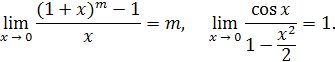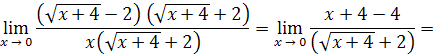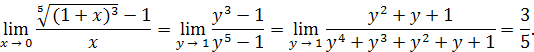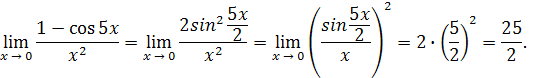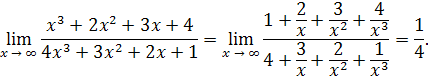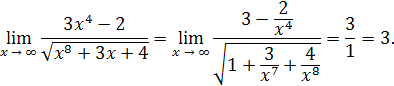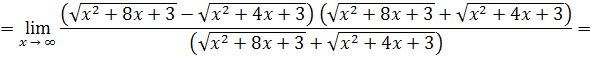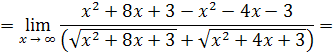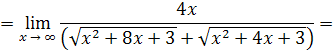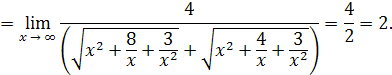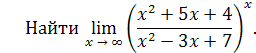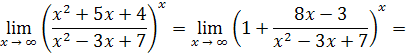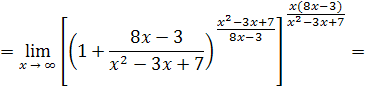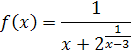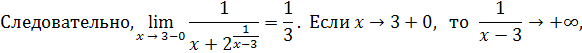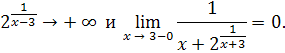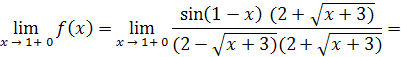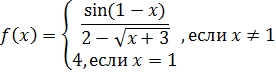|
Рефератыкосмонавтике административному праву хозяйственному праву устройствам экологическому праву криминалогия гражданский и землепользование обществознание |
Учебное пособие: Введение в математический анализУчебное пособие: Введение в математический анализМинистерство образования и науки Российской Федерации Федеральное агентство по образованию Государственный технический университет ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ Учебное пособие по математике для студентов всех специальностей заочной формы обучения 2007 ФУНКЦИЯ ОДНОЙ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ Основные определения и понятия Одним из основных понятий математики является число. Числа целые и дробные, как положительные, так и отрицательные, вместе с числом ноль называются рациональными числами. Рациональные числа могут быть представлены в виде конечных или бесконечных периодических дробей. Числа, которые представляются в виде бесконечных, но непериодических дробей, называются иррациональными. Совокупность всех рациональных и иррациональных чисел называется множеством действительных, или вещественных чисел. Действительные числа можно изображать точками числовой оси. Числовой осью называется бесконечная прямая, на которой выбраны: 1) некоторая точка О, называемая началом отсчёта; 2) положительное направление, указываемое стрелкой; 3) масштаб для измерения длин. Между всеми действительными числами и всеми точками числовой оси существует взаимно–однозначное соответствие, т.е. каждому действительному числу соответствует точка числовой оси и наоборот. Абсолютной величиной (или модулем) действительного числа x называется неотрицательное действительное число ׀x׀, определяемое следующим образом: ׀x׀ = x, если x ≥ 0, и ׀x׀ = –x, если x < 0. Переменной величиной называется величина, которая принимает различные численные значения. Величина, численные значения которой не меняются, называется постоянной величиной. Переменная величина
называется упорядоченной, если известна область её изменения и про
каждое из двух любых её значений можно сказать, какое из них предыдущее и какое
последующее. Частным случаем такой величины является числовая
последовательность Переменная величина называется возрастающей (убывающей), если каждое её последующее значение больше (меньше) предыдущего. Возрастающие и убывающие переменные величины называются монотонными. Переменная величина называется ограниченной, если существует такое постоянное число M > 0, что все последующие значения переменной, начиная с некоторого, удовлетворяют условию: – M ≤ x ≤ M, т.е. ׀x׀ ≤ M. Переменная величина y называется (однозначной) функцией переменной величины x, если каждому значению переменной величины x, принадлежащему множеству действительных чисел X, соответствует одно определённое действительное значение переменной величины y. Переменная x называется в этом случае аргументом, или независимой переменной, а множество X – областью определения функции. Запись y = f(x) означает, что y является функцией x. Значение функции f(x) при x = a обозначают через f(a). Область определения
функции в простейших случаях представляет собой: интервал (открытый
промежуток) (a, b), т.е. совокупность значений x, удовлетворяющих условию a < x < b; сегмент (отрезок или замкнутый промежуток)
Графиком функции y = f(x) называется геометрическое место точек плоскости xOy, координаты которых удовлетворяют уравнению y = f(x). Функция f(x) называется чётной, если Функция f(x) называется периодической, если существует
такое положительное число T,
называемое периодом функции, что для любого значения x выполняется равенство Наименьшим же периодом функции называется наименьшее положительное число τ, для которого f(x + τ) = f(x) при любом x. Следует иметь в виду, что f(x + kτ) = f(x), где k – любое целое число. Функции задаются: 1)
аналитически (в
виде формулы), например, 2) графически (в виде графика); 3) таблично (в виде таблицы), например таблица логарифмов. Основными элементарными функциями являются следующие, аналитически заданные функции: 1.
Степенная
функция: 2.
Показательная
функция: 3.
Логарифмическая
функция: 4. Тригонометрические функции: y = sin x, y = cos x, y = tg x, y = ctg x, y = sec x, y = cosec x. 5. Обратные тригонометрические функции: y = arcsin x, y = arccos x, y = arctg x, y = arcctg x, y = arcsec x, y = arccosec x. Если y является функцией от u, а u есть функция от x, то y также
зависит от x. Пусть y = F(u), u = φ(x). Тогда y = F(φ(x)). Последняя функция называется функцией от
функции, или сложной функцией. Например, y = sin u,
u = Элементарной функцией называется функция, которая может быть задана одной формулой вида y = f(x), где выражение f(x) составлено из основных элементарных функций и постоянных при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции. Например, y = ׀x׀ = Пример 1. Найти Решение. Найдём значения данной функции при x = a и x = b:
Тогда получим
Пример 2. Определить, какая из данных функций чётная или нечётная: а) г) Решение. а) Так как
б) Имеем f(– x) = f(x). Следовательно, функция чётная. в) Здесь f(– x) = f(x). Следовательно, функция чётная. г) Здесь Пример 3. Найти область определения функции Решение. Функция Пример 4. Найти область определения функции Решение. Функция определена, если x – 1 ≠ 0 и 1+ x > 0, т.е. если x ≠ 1 и x > – 1. Область определения функции есть совокупность двух интервалов: ( – 1, 1) и (1, + ∞). Пример 5. Найти область определения функции
Решение. Первое слагаемое
ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ При построении графиков функций применяются следующие приёмы: а) построение «по точкам»; б) действия с графиками (сложение, вычитание, умножение графиков); в) преобразования графиков (сдвиг, растяжение). Исходя из графика функции y = f(x), можно построить графики функций: 1) y = f(x – a) – первоначальный график, сдвинутый вдоль оси Оx на величину a; 2) y = f(x) + b – тот же график, сдвинутый вдоль оси Oy на величину b; 3) y = A · f(x) – исходный график, растянутый в A раз вдоль оси Oy; 4) y = f(kx) – тот же график, сжатый в k раз вдоль оси Ox. Таким образом, можно по графику функции y = f(x)
построить график функции вида
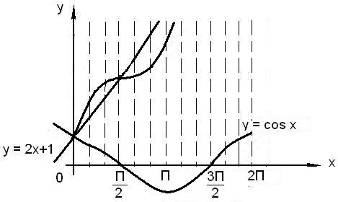
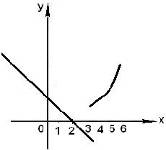
Рис. 1 Пример 6. Построить график функции y = 2x + 1 + cos x. Решение. График данной функции можно построить путём сложения графиков двух функций: y = 2x + 1, y = cos x. График первой функции есть прямая, её можно построить по двум точкам, график второй функции–косинусоида(Рис. 1). Пример 7. Построить график функции Решение. При x < 3 графиком является луч прямой, а при x ≥ 3 – ветвь параболы. Искомый график изображен на рис. 2.
Рис. 2 Пример
8. Построить график функции
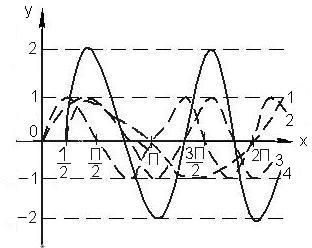
y = 2 sin (2x
– 1) или Решение. Здесь
Рис.3 ПРЕДЕЛЫ Число а называется пределом последовательности
Число
A называется пределом функции f(x) при x → a, если для любого сколь угодно малого
ε > 0 найдётся такое δ > 0, что ׀f(x) – A׀ < ε при
где M – произвольное положительное число . В этом случае функция f(x) называется бесконечно большой величиной при x → a.
Если x < a и x → a, то условно пишут x → a – 0; если x > a и x → a, то пишут x → a + 0.
делом функции f(x) в точке a.
Практическое вычисление пределов основывается на следующих теоремах.
4) 5) Используются также первый и второй замечательные пределы: 1) 2) Логарифм числа x по основанию e называется натуральным логарифмом и обозначается ln x. При решении примеров полезно иметь в виду следующие равенства:
Пример 9. Показать, что при n→∞ последовательность Решение. Здесь n–й член последовательности Пример 10. Показать, что при n → ∞ последовательность 7/3, 10/5, 13/7, . . . , (3n + 4) /(2n + 1), . . . имеет пределом число 3/2. Решение. Здесь 5/ Положив ε = 0,1,
заключаем, что неравенство Неравенство Неравенство Пример 11.
Решение. Так как x → 4, то числитель дроби стремится к числу 5 · 4 + 2 = 22, а знаменатель к числу 2 · 4 + 3 = 11.
Пример 12.
Решение. Числитель и знаменатель дроби безгранично возрастают при x → ∞. В таком случае
говорят, что здесь имеет место неопределённость вида Разделив на x числитель и знаменатель дроби, получаем
Пример 13.
Решение. Здесь числитель и знаменатель дроби стремятся к нулю при x → 3 (принято говорить, что
получается неопределённость вида
Пример 14.
Решение. Разложим на множители числитель и знаменатель дроби:
Пример 15.
Решение. Имеем
Числитель дроби стремится к 300, а знаменатель стремится к нулю, т.е. является бесконечно малой величиной, следовательно, рассматриваемая дробь –бесконечно большая величина и
Пример 16.
Решение. Умножим числитель и знаменатель дроби на сумму
Пример 17.
Решение. Положим
Пример 18.
Решение. Имеем
Пример 19.
Решение. Имеем
Здесь мы воспользовались результатом предыдущего примера, приняв
Пример 20.
Решение. Разделим числитель и знаменатель
дроби на старшую степень x,
т.е. на
Пример 21.
Решение. Разделим числитель и знаменатель на
Пример 22.
Решение. Умножим и разделим рассматриваемое выражение на
Пример 23.
Решение. Делением числителя дроби на знаменатель выделим целую часть:
Таким образом,
так как
то
Приняв во внимание, что
Пример 24. Найти левый и правый пределы функции
при x → 3. Решение.
Пример 25. Найти левый и правый пределы функции
x → a. Решение.
НЕПРЕРЫВНОСТЬ ФУНКЦИИ Функция f(x) называется непрерывной в точке а, если: 1) эта
функция определена в некоторой окрестности точки а; 2) существует
Обозначая
тогда, когда в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. Если функция непрерывна в каждой точке некоторой области (интервала, сегмента и т.п.), то она называется непрерывной в этой области. Точка а, принадлежащая области определения функции или являющаяся граничной для этой области, называется точкой разрыва, если в этой точке нарушается условие непрерывности функции. Если существуют конечные пределы:
причём не все три числа В частности, если левый и
правый пределы функции в точке а равны между собой: Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода. В точках разрыва II рода не существует хотя бы один из односторонних пределов. Сумма и произведение конечного числа непрерывных функций есть функция непрерывная. Частное от деления двух непрерывных функций есть функция непрерывная во всех точках, где делитель не равен нулю. Пример 26.
Решение. Находим
Таким образом, функция
при Пример 27.
Решение.
Итак, при
Рис. 4 Рис. 5 Разность между правым и левым пределом в точке разрыва I рода
(рис. 5). Пример 28.
Решение. В точке
может быть сокращена на
Таким образом, при
Пример 29. Доказать, что функция Решение. Находим
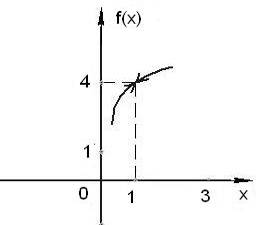
Значит, функция Пример 30. Исследовать на непрерывность функцию
и изобразить график функции в окрестностях точки разрыва. Решение. Знаменатель Для определения типа
разрыва надо найти пределы функции слева и справа при
Таким образом, пределы
функции слева и справа при
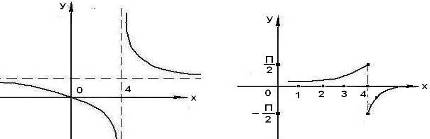
Рис. 6 Доопределив функцию
|
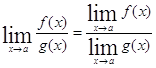 при (
при (