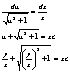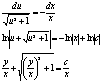|
Рефератыкосмонавтике административному праву хозяйственному праву устройствам экологическому праву криминалогия гражданский и землепользование обществознание |
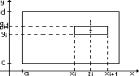
Шпаргалка: Билеты по математикеШпаргалка: Билеты по математикеБилет №1 Пусть в обл. P плоскости XOY задана некоторая фун-ия z=f(x;y). Разобъём обл. P на n частичных обл. Рi , где i=1…n, возмём произвольную точку обл. (xI;hI) Î Рi , l - наиболь-ший диаметр чатичных обл. Построим частичную сумму – сумму Римена.
Определение:
Если существует конечный предел и не зависит от способа делений области на части и от выбора т. (xI;hI) в каждой из частичных областей, то такой предел принято называть двойным интегралом по обл. Р и пишут:
В случае, если фун-ия f > 0 мы приходим к геометрическому смыслу двойного интеграла: днойной интеграл – это объём некоторого цилиндрического тела, сверху ограниченного пов-тью z = (x;y), которая проектируется на плоскость XOY в обл. Р, а образующие параллельны OZ. Площадь обл. Р:
Двойной интеграл от f(x;y) имеет многие св-ва, аналогичные св-ам одномерного интеграла. Св-ва двойного интеграла: 1.Необходимым условием сущ. Двойного интеграла явл. ограниченность ф-ции f в обл. Р, т.е если сущ. интеграл, то f(x;y) – ограниченная. 2.Всякая непрырывная ф-ция, заданная в обл. Р, интегри-руема. 3.Если ф-ция f(x;y) в обл. Р имеет разрывы на конечном числе непрырывных кривых, принадлежащих этой обл., то f интегрирума по обл. Р. 4.Сумма Дарбу:
Теорема: Для того, чтобы двойной интеграл от ограниченной обл. Р существовал, необходимо и достаточно, чтобы выполнялось равенство:
5.Аддетивность двойного интеграла, т.е., если задана обл.Р некоторой непрырывной кривой разбита на две обл-ти Р1иР2 не имеющих общих точек, то, если двойной интеграл по обл. Р существует, то существуют интегралы относительно по двум областям.
6.Линейность:
7.Если f(x;y) £ g(x;y) для "(x;y)ÎP и ф-ции f и g интегрируемы, то соответственно справедливо неравенство:
9.Если f(x;y) удовлетворяет нер-вам m £ f(x;y) £ M, то справедливо следующее неравенство:
10.Для двойного интеграла имеет место теорема о среднем: если z = f(x;y) – ф-ция, заданая в обл. Р и такая, что во всех точках этой области выполняется нер-во m £ f(x;y) £ M, где
то существует число m такое, что справедливо равенство:
В случае непрырывности ф-ции:
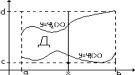
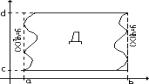
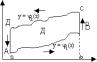
Пусть в плоскости XOY задана плоскость Д, ограничен-ная следующими кривыми: y=j1(x) a £ x £ a – снизу; y=j2(x) a £ x £ b – сверху; x = a – слева; x = b – справа; Тогда имеет место следующая теорема. Теорема: Если функция f(x;y) задана в области Д такова, что существует двойной интеграл
для любого фиксированного xÎ [a ; b] существует одно- мерный интеграл
то тогда существует повторный интеграл
Доказательство:
Обозначим c=inf j1(x) a £ x £ b; d=max j1(x) a £ x £ b и рассмотрим прямоугольник R=[a,b;c,d]ÉД. P=RД (раз- ность множеств). Построим вспомогательную функцию
Рассмотрим
Получаем следующее равенство:
Замечание: Пусть теперь область Д ограничена следующими линиями:
x=y1(y) c £ y £ d – слева; x=y2(y) c £ y £ d – справа; x = c – сверху; x = d – снизу. И пусть
Тогда аналогично предыдущему можно показать, что существует повторный интеграл и
Если же функция f(x;y) такова, что существует двойной интеграл, существует оба повторных, то одновременно имеют место формулы (1) и (2) и можно пользоваться любой из них.Вопрос №5 Формула Грина.
Теорема: Пусть задана область Д огран. след. кривыми: y=j1(x) a £ x £ b y=j2(x) a £ x £ b x=a , x=b, где ф-ции j1 и j2 непрер. на (a,b). Пусть в этой области задаётся
функция P(x,y)
– непрер. и имеющая непрер. частную производную:
Доказательство: Рассмотрим двойной интеграл,
стоящий справа в формуле(1). Т.к. под интегралом стоит непрер. функция, то
такой двойной интеграл существует, также существует одномерный интеграл
Теорема: Пусть задана область Д огран.:
y=j1(x) с £ x £ d y=j2(x) c £ x £ d x=c , x=d. И пусть в этой области задаётся
функция Q(x,y)
– непрер. и имеющая непрер. частную производную:
Cкладываем формулы (1) и (2) и получаем следующую формулу Грина для области Д:
D P(x,y), Q(x,y)
Вычисление площадей через крив интеграл
Применим ф. Грина, т.е. выразим его через криволинейный интеграл по границе области. 1. Q = x P = 0 2. Q = 0 P = -y Суммируем 1 и 2 : Пример: Вычислить площадь эллипса
Сделаем замену переменных
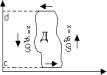
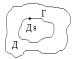
Вопрос №6 Неприрывную кривую назыв. простой кривой (жордановой), если она не имеет точек самопересечения. Областью называется всякое открытое связаное мн-во, т.е. такое мн-во всякая точка кот. явл. внутренней и любые две точки этого мн-ва можно соединить непрерывной кривой все точки кот. принадлежат данному мн-ву. Область называется односвязной областью, если внутренность всякой замкнутой кривой содержит только точки данного мн-ва. Теорема 1. Пусть Д ограниченная односвязная область пл-ти x и y, тогда для того чтобы криволинейный интеграл
был равен нулю по любой
замкнутой кривой ГÌД, (где P(x,y)
и Q(x,y)
непрерыв. И имеет непрерыв. Частные производ.
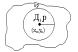
f(x,y)eД. Док-во: Пусть во всей области Д вып. Равенство (2) и Г произвольная простая замкнутая кривая принадлеж. области Д. Обознач. Через обл. Д1 кот. огранич. Эта кривая Г. Применим к этой области формулу Грина:
Предположим, что интеграл равен нулю, а равенство (2) не вып. По крайней мере в одной точке (x0 ,y0) e Д
F(x0,y0)>0 , т.к. частные произв. Непрерывны в обл. Д, то ф-ция F(x,y) непрывна в этой обл. , а из этого вытекает , т.к. F(x0,y0)>0, то существует окрестность этой точки такая, что F(x,y)>0 для всех точек лежащих в нутри окр. gr кот. явл. Границей нашей окружности. Множество точек леж. В этой окр. обознач. Д1 и применим к области Д1 ф-лу Грина:
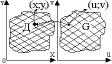
это показывает, что не сущ. ни одной точки, где бы (2) не выполнялось. Вопрос №4 Пусть заданы 2 плоскости с введенными в прямоугольник декартовыми системами координат
XOY и UOV. Пусть в плоскисти XOY задана область DV ограниченная кривой Г, а в плоскости UOV задана область G ограниченная кривой L Пусть функция Будем предпологать , что функции x и y такие, что каждой точке области G соответствует точка области D и причем это соответствие такое, что различным точкам области D соответствуют различные области точки G. Причем всякая точка области D имеет единственный прообраз (u,v) в области G. Тогда существует обратная
функции которая взаимноодназначно отображает область D в области G. Т.к. заданием двух точек U,V одназначно определяют т.(x,y) в области D, то числа U и V принято называть координатами точек в облати D, но уже криволинейными. Будем предпологать, что функции x(U,V) и y(U,V) имеют непрерывные частные производные по своим переменным x’y и y’x, x’v и y’v, тогда определитель функции имеет вид: Принято называть якобианом для функций x(U,V) и y(U,V). Можно показать,что площадь области D задана в плоскости XOY может быть выражена в криволинейных координатах следующим образом:
Замена переменных. Теорема: Пусть Z=f(x)
– непрерывная функция заданая в области D
и область D является образом области G
через посредства функций
Док-во: Разорвем обл.G непер. Кривыми на конечное число частичных областей. Тогда согласно формулам отображающим область G в обл. D. Эти кривые обл. G отображ. В некоторые кривые обл. D, т.е. обл. D будет разбита на конечное число (такое же как и обл. G) частичных подобластей.
Di – подобласти, i=1,2,…,n. В каждой обл. Di выберем т.(x,y)eDi и составим интегральную сумму Римана для двойного интеграла от функции f обл. D.
Площадь обл. Di выразим в криволинейных координатах
xi=x(Ui,Vi) yi=y(Ui,Vi)
И того, что интеграл от функции f(x,y)dxdy сущ., то $ lim sn(f)
и этот lim не зависит от выбора точек в обл. Di,
но тогда в качестве f(xi,yi) может быть взята точка
Мы получаем интегральную сумму Римана для интегр., что стоит справа формулы (1), поэтому переходя к lim в следующем равенстве:
получим ф-лу (1), т.к. суммы стремятся к соответствующему интегралу.Вопрос №2 Теорема: Пусть z = f(x,y) – ограниченная функция, заданная на прямоугольнике R = [a,b;c,d], и существует двойной интеграл по
этому прямоугольнику Если для " X [a,b] существует одномерный интеграл
то $ повторный интеграл Доказательство:
Разобьем отрезки ab и cd отрезками a=x0<x1<…<xn=b, c=y0<y1<…<yn=d. Рассмотрим теперь частичный прямоугольник Rik=[xi,xi+1;yi,yi+1] mik=inf f(x,y) Mik=sup f(x,y) Rik Rik На промежутке [xi;xi+1] возьмём точку x. Будем рас- сматривать точки, лежащие на прямой x = x. Получаем следующее неравенство mik£ f(x;y)£ Mik yk£ y£ yk+1 Проинтегрируем его по отрезку [yk; yk+1]
Замечание: если же существует двойной интеграл и существует одномерный интеграл
то существует повторный
Если же функция f(x;y) такова, что существует двойной интеграл по области R, существуют оба од- номерных J(y) и Ί(x), то одновременно имеют место формулы (1) и (2)
Например: если f(x;y) непрерывна в области R, то, как известно двойной интеграл, и оба одномерных существуют, а значит, справедлива формула (3) и для вычисления двойного интеграла можно пользоваться одной из формул (1) или (2), а именно выбирая ту или иную, которая даёт более простое решение. 7.Независемость криволинейного интегр. от пути интегрирования. Теор.1 и 2. Теорема 1. Пусть D – ограниченная одно-связанная область плоскости XOY тогда что бы
криволинейный интеграл Док-во достаточность: Пусть во всех точках обл. D выполнено рав-во (2) и пусть Г произвольная простая замкнутая кривая, принадлежащая области. Обозначим через D область кот-ю ограничивает эта кривая Г. Применим теперь к этой области ф-лу Грина. Необходимость: Криволинейный
интеграл в любой замкнутой простой кривой существует область D=0. Покажем, что во всех точках области D выполняется рав-во (2). (это доказуется методом от
противного). Пусть интеграл = нулю, а
рав-во (2) не выполняется, по крайней мере, в одной точке
Теорема 2 Пусть D есть односвязная область плоскости XOY в этой области заданы две непрерывные функции D(x,y)
и Q(x,y)
имеющие непрерывные частные производные Док. Не обход. Пусть криволинейный интеграл не зависит от пути интегрирования, а зависит от начальной и конечной точки пути интегрирования. Возьмём в области D произвольно простую замкнутую кривую Г. На этой кривой т. А и т. В Т.к. по условию криво-ный интеграл не зависит от пути интегрирования, то интеграл по кривым АmB=AnB
Док. Достат. Пусть выполняется рав-во (2) . Покажем, что криволенейный интеграл не зависит от пути интегрирования : 1-й случай. Берём две произвольные точки принадлежащие области D и соединяем эти
точки непрерывными кривыми Если эти кривые образуют простой
замкнутый контур без самопересечения и т.к. выполняется рав-во (2), то интеграл
поэтому замкнутому контуру обязан быть равен 0. 2-й случай. Пусть
Будем двигаться от А к C1 в результате получили контур 3-й случай. Если кривые пересекаются на счётном множестве точек то интеграл по таким кривым тоже будут равны между собой ….счётное множество эквивалентное множеству натуральных чисел.9.Параметрические ур-я поа-ти, касательная плос-ть, нормаль, направляющие косинусы нормали. Пусть поверхность задана параметрическими уравнениями :x=x(U,V) ; y=y(U,V); z=z(U,V) и функции x,y,z непрерывны и имеют непрерывные частные произвольные. Рассмотрим матрицу На поверхности берём точки U0(x0,y0,z0) которая является образом (U0,V0) l- угол образованный нормалью с направлением осью X m- угол образованный нормалью с направлением осью Y n- угол образованный нормалью с направлением осью Z, cos l cos m cos n - называют направляющими косинусами нормали. Для направляющих косинусов нормали имеет место формула:
Билет 12 Задача о вычислении массы пространств-го тела. Пусть в трехмерном пространстве задано тело D, причем в точках этого тела определены некоторые массы и известна плотность распределения массы, кот. явл-ся ф-цией трех переменных U=R(x,y,z).Разобьем это прост-ное тело некоторыми гладкими пов-ми на конечное число областей D1, D2,…,Dn. В каждой области Di произвол. выберем некот. точку (x,h,e)Î Di. Плотность массы в этой точке – это R(xi,hi,ei). Будем считать, что ф-ция R явл-ся непрерывной, а разбиение достат. мелким так, что значения ф-ции внутри области Di не слишком отличаються от значений ф-ции R в выбранной точке. Т.е. будем считать, что в области Di плотность массы одна и та же и равна числу R(xi,hi,ei). Тогда очевидно масса, заключенная в обл. Di , будет равняться R(xi,hi,ei) * DV. Тогда приближенное значение массы для всей области равна S R(xi,hi,ei)*DVi Пусть l - наибольший из диаметров Di – тых областей, а тогда масса , заключенная в области равна m=lim(l®0) S R(xi,hi,ei) * DVi Пусть теперь задано пространств. тело D. В точках этого тела определена ф-ция U=f(x,y,z). Разобьем это тело на конечное число Di –тых (i=1,2,3,…). В каждой области Di выберем произвол. точку (xi,yi,zi) и составим интегральную sn=S ò(xi,yi,zi) * DVi Если сущ. предел и он конечный и он не зависит от способа деления обл. D на части и выбора точек (xi,yi,zi) , то этот предел называют тройным интегралом по обл.D от ф-ции f(x,y,z)lim(l®0)sn=òòò f(x,y,z)dx dy dz Следовательноm=òòòR(x,y,z)dxdydz Св-ва тройного интеграла аналогично св-м двойного интеграла 1) Всякая интегрируемая в обл. D ф-ция ограничена в этой области. 2) Могут быть построены суммы Дарбу верх St=S Mi * DVi низ st=S mi * DVi 3) Необходимо и достаточное условие сущ. интеграла lim(l®0)( St-st)=0 4) Как и в случае двойного интеграла сущ. тройной интеграл от любой непрерывной ф-ции, заданной в обл. D. Однако тройной интеграл сущ. и в случае, когда ф-ция f(x,y,z) имеет разрывы 1-го рода на конечном числе пов-тей данного тела D. 5)Тройной интеграл обладает св-вами линейности и аддетивности òòòDfdx = òòòD1fdx + òòòD2 , где D=D1ÇD2 6)Если сущ. тройной интеграл от ф-ции f, то сущ. интеграл по модулю и существует равенство ôòòòô£ òòòôfôdv Если функция fв области D ограничена какими-то числами m £ f £ М , то для тройного интеграла справидливо неравенство mVd £òòò ¦dv£M VD 7) Имеет место теорема о среднем , т.е. если функция ¦(x,y,z) не-прерывная в области D , то справедливо равенство òòò ¦dv = ¦ (X0 , Yo , Z0) (X0 , Yo , Z0)ÎD Ввычесление тройного интеграла по параллепипеду . 1. Пусть функция ¦(x , y ,z) задана на параллепипеде R[ a ,b ; c , d; e, f]. Обозначим через Gи D прямоугольника D[ c , d; e, f] и [a,b;c,d] . Тогда если существует тройной интеграл по параллепипеду от функции ¦(x,y,z) и существует для любого x из [a,b] двойной интеграл по прямоугольнику D òò ¦(x,y,z)dydz то существует òòò¦dv =òdxòò¦(x,y,z)dydz Если для " zÎ[e,f] $ òò ¦(x,y,z)dxdy,то
òòò ¦dv = òdxòò¦(x,y,z)dydz = òòdxdyò¦(x,y,z) . Если функция ¦(x,y,z) непрерывна в области D,т.е.
на параллепипеде , то все указаные ранее интеграмы существует и имеет место вся большая формула и в последнемравенстве можно менять местами в случае непрерывности функции. 2. Пусть ¦(x,y,z) задана в пространстве области G причем область G сверху ограниченная плоскостью z=z2(x,y) снизу z=z1(x,y),a c боков ограничена цилиндрической поверхностью образующая которой ½½OZ. И пусть проекция этого тела на плоскость XOY есть некотокая область D .Тогда можно показать ,что тройной интеграл по пространственной области G может быть вычеслен по такой формуле
Продолжение №12 Если теперь обл. D будет иметь следующее строение. Пусть обл. D, кот. явл. проэкцией тела на пл-ть XOY, ограничена следующими линиями: отрезками прямых x=a и x=b , и кривыми y=j1
(x) и y=j2(x). Тогда тройной интеграл:
Пусть в пространстве задана поверхность Q, которая является гладкой и задана явным уравнением z = f(x;y), где (x;y)ЄD. D является проэкцией поверхности Q на плоскость xoy. Будем считать f(x,y) – непрерывная со своими частными производными
Требуется вычислить площадь S заданной поверхности. Разобьем область D непрерывными кривыми на конечное число частичных областей D1,D2,…,Dn. Возьмем в области Di т.(xi;yi) и построим цилиндрическое тело, в основании которого лежит область Di , а образующие параллельны оси oz. Это цилиндрическое тело вырежет на нашей поверхности Q некоторую i-тую площадку. Обозначим через Mi (xi;yi;zi) точку на i-той частичной поверхности такую, что zi=f(xi;yi), т.е. Mi(xi;yi;z (xi;yi)). Так как частные производные p,q-непрерывны, то поверхность является гладкой и в каждой точке этой поверхности существует касательная плоскость. Проведем теперь касательную плоскость к поверхности в точке Mi. Построенное тело на обл. Di на этой плоскости Т вырежит некоторую площадку Ti. Eе площадь STi дает некоторое приближение для площади куска поверхности, который вырезается этом цилиндрическим телом. Аналогичным образом поступим с остальными областями D1,D2,…,Dn. В результате мы получим некоторое приближение для площади всей заданной поверхности. Пусть n d n=å STi i=1 А тогда принято считать, что площадью поверхности является n S=lim d n=lim å STi , l®0 l®0 i=1 где l - наибольший из диаметров площадей Di. Нетрудно показать, что такой предел будет равен S=lim dn=òò (1/½cos n½)dx dy, l®0 D где n - угол, образованный нормалью к поверхности с осью oz. Доказательство:
Через ni обозначим угол, который образует касательную плоскость с плоскостью xoy. В точке Mi проводим нормаль к поверхности. Получаем, что угол, образованный касательной плоскостью с плоскостью xoy равен углу, образованному нормалью к поверхности с осью oz. Площадь Di есть проекция плоскости Ti , которая лежит на касательной плоскости. А тогда SDi=STi*½cos ni ½. А тогда получаем, что n n n d n=å STi=å SDi / ïcos n i ï=å (1/ïcos niï)*SDi . i=1 i=1 i=1 Получили, что данная сумма является суммой Римена для такого двойного интеграла: òò (1/ïcos nï)dx dy. D Получили , что площадь поверхности Q , заданной явным уравнением , вычисляется по такой формуле : SQ=òò (1/ïcos nï)dx dy. D Если поверхность задана явным уравнением , то cos n=1/±Ö (1+p2+q2 n)=1/Ö(1+zx'2+zy'2 ). В случае явного задания поверхности SQ=òòÖ(1+zx'2+zy'2)dx dy =òòÖ(1+p2+q2)dx dy D D Если теперь поверхность Q задана параметрическими уравнениями x=x(u,v) y=y(u,v) (u,v)єG , z=z(u,v) где функции x,y,z непрерывны со своими частными производными, то в этом случае площадь поверхности вычисляется по следующей формуле 6SQ=òòÖ(A2+B2+C2) du dv, где А,B,C-есть раннее введенные функциональные определители. 8.Касательная пл-ть к пов-ти и её ур-е в случае явного и не явного задания пов-ти. 1) не явное. Пусть поверхность задаётся не явным уравнением F(x,y,z)=0. Эта функция непрерывна и имеет непрерывные частные производные. Здесь рисунок. Зафиксируем любую точку M0(x0,y0,z0). Рассмотрим кривую проходящую через эту точку. Пусть
уравнение этой кривой будет x=x(t)
y=y(t)
z=z(t)
где 2) явно. пусть пов-ть задаётся явным
ур-ем z=f(x,y), где (x,y) z-f(x,y)=0; F(x,y,z);
Вопрос№11 Если пов-ть Р задана параметрич. ур-ями
ф-ии x,y,z непрерывны с частными производными то поверхностный интеграл 1-го рода вычисл. С помощью интеграла двойного рода,взятого по обл. G по ф-ле:
Если пов-ть Р задается явным урав. Z=F(x,y)=z(x,y) Где (x,y) Часными произв.,то поверхностный интегр.1-го рода Вычисл.по ф-ле :
где P и Q соотв.часные произв. Поверхн.интеграл 2-го рода
Криволин.интеграл 2-го рода:
Пусть задана двусторонняя пов-ть S и на верхн. Стороне задана ф-ция U=F(x,y,z).Разобьем задан. Повер.S непрерывн.кривыми на конечное число Частичных поверх. S1,S2….Sn.Проэктир.эти поверх. На XOY
,
Если сущ.предел Lim s n при От способа дел.области на части и выбора точек Mi, То его наз.повер.интегалом 2-го рода по поверхн.и Обознач. :
Если же проэктировать пов-ть на другие плоскости ,то Получится:
Пусть на пов-ти заданы три ф-ции P(x,y,z), Q(x,y,z) R(x,y,z) тогда повер.интегр.2-го рода общего вида наз.
Сущ. Пл-ть такая что в каждой т.пов-ти сущ.нормаль.Обозначим Через Тогда,как и для криволин.интеграла имеет место форма между повер.Интегр.1 и 2 рода:
Пусть пов-ть S задается своими парам.ур-ми:
ф-ции x,y,z –непрерыв.и имеют непрер.частн. произв.Тогда:
Пов-ти с повер.интегралом 2-го по задан.пов-ти. Пусть задана некоторая гладкая повер.S на верхн.стороне этой повер. Заданы три ф-ии P(x,y,z),Q(x,y,z),R(x,y,z) непрерыв.и имеющ.непрер. Частн.произв.по своим аргументам и L-контур повер.,проходящий в Полож.направления.Тогда:
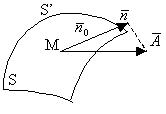
Поток вектора через поверхность Пусть задана некоторая
область(тело) ДÌR3
Пусть над этой областью определено поле вектора
Возьмем в области Д некоторую
поверхность S обозначим через
Потоком вектора
Проекция вектора на ось
Ап – проекция вектора А тогда поток вектора будет равен
Общий вид диф уравнения F(x, y, y’)=0 y’=f(x,y) (1). Решением дифференциальное уравнение первого порядка называется всякая функция y=j(x), которая будучи подставлена в данное уравнение обращает его в тождество. j’(x)= f (x, j(x));
Задача Коши для диф. уравнения 1 порядка. Требуется найти решение диф.
ур-я (1) удовлетворяющего следующему условию Теорема Коши. Пусть задана на плоскости XOY некоторая обл. Д и задано диф. ур-е разрешённое
относительно производной, тогда если функция f(x, y) и её частная производная принимает значение
Т.е. если существует решение диф. ур-я, то таких решений бесконечное множество. График функции являющийся решением диф. ур-я принято называть интегральной кривой, процесс решение принято называть интегрированием. Точку Решения диф. ур-я в каждой т. которого нарушается условие единственности из теоремы Коши, принято называть особым решением диф. ур-я. График особого решения называется особой кривой. Определение общего решения диф. ур-я 1 порядка: Функция y=j(x, C), где С произвольная константа, называется общим решением диф. ур-я (1) если выполнены следующие условия: Функция y=j(x, C) является решением ур-я (1) при любом значении произвольной константы С; Какова бы ни была т. Частным решением данного диф. ур-я называется решение этого ур-я которое может быть получено из общего решения при некотором фиксированном значении произвольной константы С. Определение: Если решение диф. ур-я (1) может
быть получено в виде Особое решение данного диф. ур-я (1) ни при каком значении константы С не может быть получено из общего решения.. Вопрос №17 Диф. ур-ем с разделёнными перемеными принято называть ур-е вида (1):
Если y=y(x) является решением ур-я (1), то и правая и левая части этого ур-я представляют собой дифференциалы от переменной x, т.е. имеем равенство двух дифференциалов, то тогда неопределённые интегралы отличается разве лишь на константу. Т.е. интегрируя равенство (1), получаем общее решение данного диф. ур-я:
Уравнения с разделяющимися переменными:
Уравнения, приводящиеся к уравнениям с разделёнными переменными.
Т.е.
Пример:
Дивергенция , циркуляция ротор вектора Пусть задана некоторая
пространственная область Д над которой определенно поле вектора Рассмотрим интеграл , выражающий поток вектора через поверхность S Обозначим Аx = P(x,y,z) , Ay =Q(x,y,z) , Az = R(x,y,z)
поверхность S ограничивает тело Д1
- расходимость (дивергенция ) вектора
- уравнение Остроградского-Гаусса Ап – проекция вектора Циркуляция , вихрь и ротор вектора Пусть в пространстве задано некоторое тело Д и пусть в теле Д рассматривается некоторая кривая L , которая гладкая , имеет непрерывно изменяющуюся касательную Обозначим через a,b,g углы , образует касательная к кривой L с осями координат Пусть над этим телом определенно
поле вектора Тогда криволинейный интеграл по кривой L
Рассуждая как и прежде можно
показать , что L0 - единичный вектор касательной L1 L1 - касательный вектор к кривой L Если кривая L является замкнутой кривой , то такой интеграл принято
называть циркуляцией вектора Пусть теперь в некоторой области Д задана поверхность S , контур которой обозначим через L
- формула Стокса
Ротором векторного поля
Циркуляцией вектора
Криволинейные интегралы в пространстве и объем тела в криволинейных координатах Пусть в пространстве OXYZзадано тело G.И пусть в другом пространстве OUVW задано тело Д И пусть заданы 3 функции
взаимно однозначно отображающие область Д в области G Будем считать функции x,y,z –непрерывными и имеющие непрерывные частные производные Рассмотрим Якобиан
Можно показать , что в случае взаимно однозначного отображения области Д и G якобиан ни в одной точке области Д не обращается в 0 А значит в области Д сохраняет один и тот же знак Координаты (U,V,W) принято называть криволинейными координатами точек области G И тогда можно показать , что объем области G в криволинейных координатах выражается по следующей формуле
Если теперь в области G будет задана функция f(x,y,z) –непрерывная в этой области, то справедлива следующая формула замены переменных в тройном интеграле
При замене переменных в тройном интеграле наиболее часто используются цилиндрические и сферические координаты Под цилиндрическими координатами следует понимать объединение полярных координат на плоскости XOY и аппликаты z r,q,z
r-расстояние от начала координат до проекции тМ на плоскость q-угол , образованный радиус вектором ОМ , в пол направлении
0£ r < +¥ , 0£ q < 2p , -¥< z < +¥ Подсчитаем якобиан в случае цилиндрических координат
q- угол , образованный проекцией радиус-вектора тМ j-угол, образованный радиус-вектором тМ r- радиус-вектор тМ, равный ОМ Сферическими координатами принято называть r,j,q Где r- расстояние от начала координат до тМ j- угол , образованный радиус-вектора с осью Z q- угол, образованный проекции радиус-вектора с осью X r=(ОМ) 0£ r < +¥ , 0£ j < p , 0 < q < 2p Найдем якобиан для сферических координат
=cosj[r2 cos2 qcosj sinj + r2 sin2 q sinj cosj] + rsinj [r sin2 j cos2 q + r sin2 j sin2 q] =r2 cos2 j sinj + r2 sin3 j=r2 sin j I(r,j,q)=r2sinj Вопрос №18 Пусть задана функция
Пример: Определение: диф. ур-е 1 порядка разрешённое относительно производной называется однородным диф. ур-ем 1 порядка, если его правая чаcть (функция f(x,y)) является однородной функцией 0-й степени. Метод решения: Пусть (1)
является однородным уравнением
2) если т.е. Билет№20 Линейные диф. Уравнения1- порядка. Метод подстановки. Линейным уравнением 1-го порядка называют уравнения вида: y’+yP(x)=Q(x) – где P(x) и Q(x) некоторые функции переменной х , а y’ и y входят в уравнение в 1 степени. 1.Метод подстановки: Будем искать решение уравнения 1 в виде произведения y=U(x)V(x) при чём так, что мы можем подобрать одну из функций по желанию, а вторую так, чтобы удовлетворяла (1) : y’=U’V+UV’ ; U’V+UV’+UV*P(x)=Q(x) ; U’V+U(V’+V*P(x))=Q(x) Найдём V ,чтобы V’+VP(x)=0 :
y’+y cos(x)=1/2 sin(2x) y=UV U’V+UV’+UVcos(x)=sin(x)cos(x) V’+Vcos(x)=0 dV/V=-cos(x)dx ln(V)= -sin(x) V=e-sin(x)
sin(x)=t
Уравнение Бернулли и Рикотти и их решение. Уравнение Бернулли – это диф. Ур-е следующего вида :
где P(x) и Q(x) – непрерывные функции m – действительное число ¹0 и ¹1 разделим уравнение на ym :
Обозначим через
теперь подставим в уравнение
получили линейное уравнение . Уравнение Рикотти – это
диф. следующего вида Где P(x),q(x),r(x) – некоторые непрерывные функции Рассмотрим несколько случаев 1) если ф-ции P(x) , Q(x) и r(x) – явл. Константами то в этом случае сущ. решением ур-я Рикотти т.к. в этом случае ур-е явл. Ур-ем с разделенными переменными .
2) если q(x)=0 имеем лин. Ур-ние 3) если r(x)=0 то имеем ур-е Бернулли Если не выполяется ни одно из этих 3 условий , то ур-е Рикотти решить нельзя , неразрешимо в квыадратурах . Однако если эти три случая , но возможно найти хотя бы одно частное решение этого ур-я то ур-е решается в квадратуре . Установим это : пусть
тогда введем новую функцию z=z(x) Положем Подставив в уравнение получим
а это ур-е Бернулли Билет №23 Уравнение в полных дифференциалах и их решение Пусть задано диф. ур-е ел. Вида:
где P(x,y) и Q(x,y) – непрер. Функции имеющие непрерыв часн. Производную 2 порядка включительно. Диф. ур. Назыв. Ур-ем в полных
диф-лах , если
т.е. ур. В этом случае имеет вид
: это уравнение явл полным диф. функции U как ф-ции двух переменных:
если выполняется равенство тогда
то левая часть
Теорема о необходимости и достаточности условия того что Ур было ур-ем в полных дифференциалах Теорема : Для того чтобы ур было ур-ем в полных диф. в некоторой Д принадл ХОУ Необх. И дост. Чтобы во всех
точках обл. Д выполн равенство
найдем Метод вариации производной постоянной при решении линейного диф. уравнения 1-го порядка. y’+P(x)y=Q(x) (1) -задано линейное неоднородное уравнение. Рассмотрим соотв. ему однородное уравнение y’=P(x)y=0 (2). Найдём общее решение:
Будем искать решение в том же виде, что и однородного, только
считая с не произвольной константой ,а функцией от х :
К таким уравнениям относят уравнения вида:
1) 2). 1). 2). Теперь допустим Билет №24 Интегральный множитель и его нахождение Пусть задано диф. ур-ние в диф. форме вида :
не всякое такое уравнение явл.
Уравнением в полных виференциалах однако доказано что для всякого такого ур-я
может быть подобрана ф-ция Найдем функцию определяющую интегр. Множитель данного уравнения:
тогда должно выполн. Рав-во:
имеем уравнение в частных производных относит неизв функции Мю.Общего метода нахожения которой не существует Найдем интегр множитель в случае если он явл ф-цией от одной из перемен. 1)Найдем условие при которых
2) Аналогично и
Вопрос №26. Уравнение вида: f(x,y¢)=0. 1) Предположим, что данное уравнение можно разрешить относительно y¢; y¢=fk(x), k=1,2,…
……………………………….
2) Пусть оно не разрешается относительно y¢ и разрешается относительно x. Пусть оно эквивал. Такому x=j(y¢). Будем искать решение данного уровнение в параметрической форме. y¢=p=p(x). Пусть x=j(p), А y ищем так: dx=j¢(p)dp dy=y¢dx=pj¢(p)dl. Отсюда Тогда общее решение 3) Предположим, что ур-ние не
разрешено не относ. х, не относ. y¢, но оно может быть представлено в виде с-мы двух ур-ний,
эквивалентных данному ур-нию: dy=y¢dx dx =j¢(x)dt dy=y(t)* j¢(t)dt Тогда парметрическое решение данное ур-я
Ур-ние Логранжа Ур. Лог.имеет следующий вид где ф-ция сменная производная по своему аргументу. Покажем что путём диф-ния и введения параметра можно получить общее решение в параметрической форме.Пусть у`=p=p(x) Подставляем в ур.
Продиф-ем на х
Рассмотрим два случая:
Будем смотреть на это ур-ние как наур-ние от неизв. Ф-ции х, которая в свою очередь явл. Ф-цией параметра р.Тогда имеем обычное инт.ур.относительно неизв.ф-ции, которую можем найти. Пусть общим интегралом этого ур.будут F(p,е,c)=0 (2) Объеденим (2) и (1)
А это и есть общее решение ,представленое через параметр Р. 2) что удовлет. решению ур. : Пусть РI(I=1,2,..) будут решением этого ур. Тогда решением первоначального ур.А. будут ф-ции которые явл. Особыми решениями ур. А. И не могут быть получены общим решением. Ур.Клеро. Ур.Клеро имеет вид
аргументу. Вводим параметр Тогда Диф-ем по Х Если подставляем в (3)и получаем:
Пример Замена
общее решение:
Билет 27. Уравнение вида F(y,y`)=0 1)Пусть ур-ние разрешимо относ. y`,тогда y`=fk(y) Разрешим относ. y, где к=1,2….
Пустьfk(y) Считаем х-функцией от у.
Пусть fk(y)=0 . Тогда решен.данного ур-я могут быть ф-ции такие,которые удовлнтв.условиюF 2)Пусть ур-ние не разр.относ.у,, но разреш. отн. y, т.е. пусть наше ур-е эквивал. Ур-нию
а)пусть
а тогда:
б) пусть у’=0, тогда у=const Решением ур-ния будут ф-ции у= какие удовлет.ур-ние F( Пример: решить ур. Разреш. относ. У .тогда
Рассмотрим несколько случаев: 1.Пусть задано следющее диф. ур-ние:
Это диф. ур-е 1-го порядка n-ой степени, где aI (x;y) – некото- рые непрырывные ф-ции двух переменных в некоторой обл. Q Ì R2 (i=0,…,n). Мы имеем ур-е n-ой степени относительно 1-ой производной, а известно, что всякое ур-е n-ой степени имеет вточности n-корней, среди которых есть как действительные так и комплексные. Пусть например это ур-е имеет какоето количество m £ n действительных корней. Т.к. коэффициенты этого ур-я являются ф-циями двух переменных, то ясно, что корни тоже будут ф-циями двух переменных. Пусть это будут решения y1=fk(x;y), k=1,2…m. Ур-е (1) свелось к m - ур-ий 1-го порядка. Пусть это ур-я, имеющие общий интеграл Fk=(x;y;c)=0, k=1,2…n. Тогда совокупность всех этих общих интегралов
и будет общим решением данного диф. ур-я (1). Пример:
Пусть x=0,а ур-ние разделим на x
Ур-я вида: F(y!)=0 Пусть заданное диф. ур-е явно зависит только от y! и не зависит явно от x и y. Тогда мы имеем некоторое алгебраическое ур-е относительно производных. А такое алгебраическое ур-е пусть имеет конечное или бесконечное множество действительных решений относительно производных. Т.е. y! = ki , i= 1,2… , где ki – некоторые действительные числа. У нас выполняется условие F(ki)º0. Решим ур-е y!=ki; y=kix+c; ki=(y-c)/x. Общий интеграл заданного диф. ур-я
Пример: (y!)4-4(y!)2+1=0 k4-4k2+1=0 действительные корни есть Значит сразу получаем общее решение
|
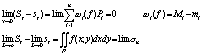
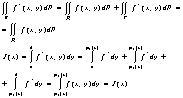
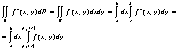
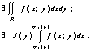
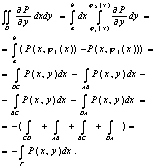
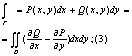
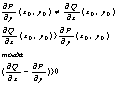
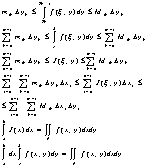
 Вопрос №10
Вопрос №10
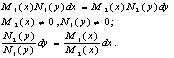
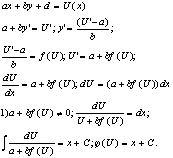
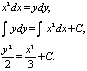 Билет №15
Билет №15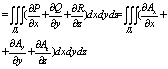
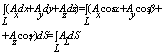
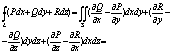
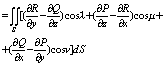
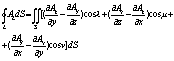
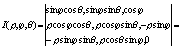
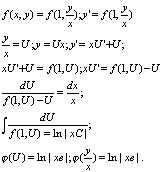
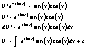
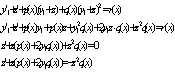
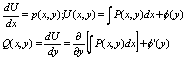
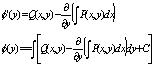 Билет№21.
Билет№21.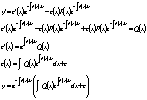 Билет№19 Уравнения,
приводящиеся к однородным.
Билет№19 Уравнения,
приводящиеся к однородным.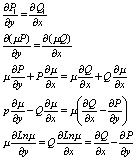
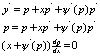
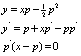
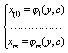 общее решен.х.
общее решен.х.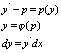
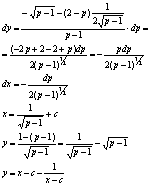 Билет 25.
Билет 25.