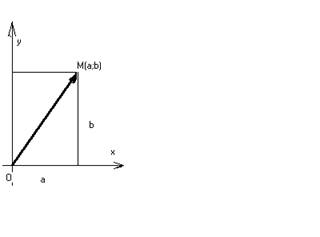
У багатьох розділах математики та її застосуваннях неможливо обмежетись розглядом лише дійсних чисел. Вже досить давно під час розв’язування різних задач виникла потреба добувати квадратний корень з від’їмних чисел. Але чисел, які піднесені до квадрату дають від’ємні числа, тоді не знали і тому вважали, що квадратні корені з від’ємних чисел не існують, тобто задачі, які до них приводять, не мають розв’язків. Зокрема, так було під час розв’язування квадратних рівнянь з від’ємним дискримінантом, наприклад:

х² - 4х + 10 = 0 х₁,₂=2±Ö-6.

Тому природно постало питання про розширення множини дійсних чисел, прєданням до неї нових так, щоб у розширеній множині крім чотирьох арифметичних дій – додавання, віднімання, множення і ділення (за вийнятком ділення на нуль), можна було виконувати дію добування кореня. Це питання було успішно розв’язано лише у ХІХ сторіччі. Відповідно до прийнятих в математиці принципів розширення поняття числа при розширенні множини дійсних чисел мають задовільнятися такі вимоги:

1) озачення нових чисел мусить спиратися на поняття дійсного числа, і нова множина має містити всі дійсні числа;

2) для нових чисел повині виконуватись п’ять законів прямих арифметичних чисел (пригадайте ці закони);

3) у новій числовій множині мусить мати розв’язок рівняння х²=-1.

Оскільки існує вимога, щоб у новій числовій множині рівняння х²=-1 мало розв’язок, необхідно внести деяке нове число, вважаючи його розв’язком цього рівняння. Число, квадрат якого дорівнює –1, позначають буквою і і називають уявною одиницею (і – перша буква латинського слова imaginarius – уявний). Підкреслимо, що рівність і²=-1 приймається за означенням і не доводиться. До нової множини мають належати числа виду bί (добуток дійсного числа на уявну одиницю) і числа виду a + bί (сумма дійсного числа a та добуток дійсного числа b на уявну одиницю).

Отже, нова множина множина чисел повина містити всі числа виду a + bί.Числа виду a + bί, де a і b – довільні дійсні числа, аί – уявна одиниця називають комплексними. Слово “комплексний” означає складений. Число a називають дійсною частиною числа a + bί , а вираз bί – уявною.

Число називають коефіцієнтом при уявній частині. Наприклад, у числі 6 + 7ί дійсна частина 6, уявна 7. Коефіціент при уявній частині дорівнює 7. Дійсною частиною числа 0 + 3ίє число нуль, а уявною – вираз 3ί; коефіцієнт при уявній частині дорівнює 3. Числа виду a + 0ί ототожнюються з дійсними числами, а саме вважають, що a + 0ί=a. Таким чином виконується обов’язкова для будь – якого розширення поняття числа вимога, щоб попередній числовий “запас” входив до нової числової множини як її частина. Множина дійсних чисел є частиною (підмножиною) множини комплексних чисел. Відповідно до вимог, що ставляться при будь – якому розширення поняття числа, при побудові множини комплексних чисел треба ввести за означенням умову рівності цих чисел і правила виконання прямих дій – додавання і множення.

Два комплексних числа a + bί і c + dίрівні між собою тоді і тільки тоді, коли a = c і b=d, тобто коли рівні їх дійсні частини і коефіцієнти при уявних частинах.

Поняття “більше” і “менше” для комплексних чисел не має смислу. Ці числа за величиною не порівнюють. Тому не можна, наприклад, сказати, яке з двох комплексних чисел більше 10ί чи 3ί, 2+5ί чи 5+2ί.

Важливим є поняття про спяжені комплексні числа. Числа a + bί і a - bί, дійсні частини яких рівні, а коефіцієнти при уявих частинах рівні за модулем, але протилежні за знаком, називають спряженими. Можна сказати простіше: числа a + bί і a - bί, які відрізняються лише знаком уявної частини, називають спряженими.

Наприклад, спряженими є комплексні числа 4+3ί та 4-3ί; 2-ί та 2+ί; -8+7ί та –8-7ί;-5-ί та –5+ί. Якщо дане число 6ί, то спряженим до нього є –6ί. До числа 11 спряженим буде 11, бо 11+0ί=11-0ί.

2. Дії над комплексними числами

а) додавання комплексних чисел

Означення: сумою двох комплексних чисел a + bί і c + dί називається комплексне число (a + c) + (b + d)ί, дійсна частина якого і коефіцієнт при уявній частині дорівнюють відповідно сумі дійсних частин і коефіцієнтів при явних частинах додатків, тобто (a + bί) + (c + dί) = (a + c) + (b + d)ί.

Приклади. Виконати додавання комплексних чисел:

1) (3+2ί) + (-1-5ί) = (3-1) + (2-5)ί = 2-3ί

2) (4-5ί) + (2-ί) = (4+2) + (-5-1)ί = 6-6ί

3) (2+3ί) + (6-3ί) = (2+6) + (3-3)ί= 8

4) (10 – 3ί) + (-10+3ί) = (10-10) + (-3+3)ί = 0

З наведених прикладів випливає, що додавання комплексних чисел ми виконуємо за правилом додавання многочленів. У множині дійсних чисел справедлива рівність a + 0 = a. У множині комплексних чисел нулем є число 0 + 0ί. Справді, яке б не було число , справедлива рівність

(a + bί) + (0+0ί) = (a +0) + (b +0)ί = a + bί

За аналогією з дійсними числами, для комплексних чисел вводиться поняття про протилежні числа: два числа a + bί та -a - bί, сумма яких дорівнює 0, називають протилежними.

Додавання комплексних чилел підлягає переставному та сполучному законам. Доведемо, наприклад, справедливість переставного закону додавання комплексних чисел. Нехай,z₁ = a + bί, z₂= c + dί. Тоді z₁+ z₂ = (a + bί) + (c + dί) = (a + c) + (b+d )ί , z₂+ z₁ = (c + dί) + (a + bί) = (c + a) + (d+b)ί. Оскільки для додавання дійсних чисел справджується переставний закон, тобто a + c = c + a; b+d = d+b, тобто (a + c) + (b+d)ί = (c + a) + (d+b)ί , то z₁ + z₂ = z₂+ z₁, що й треба було довести. Означення суми комплексних чисел поширюється і на випадок трьох і більше доданків.

б) віднімання комплексних чисел

Віднімання комплексних чисел означають як дію, обернену до додавання, коли за даною сумою й одним з доданків знаходять другий, невідомий доданок.

Означення. Різницею двох комплексних чисел z₁= a + bί і z₂ = c + dί називається таке комплексне число z₃= x+yί , яке в суммі з z₂ дає z₁.

Отже, z₁- z₂= z₃, якщо z₃ + z₂= z₁. можливість дії віднімання комплексних чисел та її однозначність потребує доведення.

Доведемо, що для будь – яких комплексних чисел z₁= a + bί і z₂ = c + dί різниця z₁- z₂ визначена і до того ж однозначно. Доведемо, що існує, і до того ж єдине, комплексне число z₃= x+yί, яке в сумі з z₂ дає z₁.

За означенням дії віднімання, (c + dί) + (x+yί) = a + bί. виконавши додавання в лівій частині рівності, дістанемо:

(c + x) + (d + y)ί = a + bί (1).

З умови рівності двох комплексних чисел маємо:

c + x = a

d + y = b

Ця система має розвиток, і до того ж єдиний: x = a - c, y = b – d. Отже, існує , і до того ж єдина, пара дійсних чисел (x, y), яка задовільняє рівняння (1), що і треба було довести. З доведеного випливає, що віднімання комплексних чисел виконують за таким правилом:

(a + bί) – (c + dί) = (a - c) + (b – d)ί

Приклади: Виконати віднімання комплексних чисел.

1) (3+4ί) – (1+2ί) = (3-1) + (4-2)ί = 2 + 2ί;

2) (-5+2ί) – (2+ί) = (-5-2) + (2-1)ί = -7+ί;

3) (6+7ί) – (6-5ί) = (6-6) + (7+5)ί = 12ί;

4) (0,3+2,5ί) – (-0,75+1,5ί) = (0,3+0,75ί) + (2,5-1,5ί) = 1,05+ί;

5) (Ö2-2ί) – (Ö2+3ί) = (Ö2-Ö2) + (-2-3)ί = -5ί;

6) 1+1/2) – (1/4-3/5) = (1/3-1/4) + (1/2+3/5) = 1/12 + 11/10.

в) Множення комплексних чисел

Означення. Добутком двох комплексних чисел a + bί і c + dί називається комплексне число (ac - bd) + (ad + bc)ί . Суть і доцільність цьго означення стане зрозумілою, якщо взяти до уваги, що цей добуток утворений так, як виконується множення двочленів з дійсними коефіцієнтами, а саме (a + bί)( c + dί) = ac + adί + bcί + bdί² = ac + (ad + bc)ί + bdί². Замінюючи, за означенням, ί²на –1, дістанемо: bdί² = -bd . Відокремивши дійсну частину від уявної, остаточно матимемо:

(a + bί)( c + dί) = (ac - bd) + (ad + bc)ί (2)

Формулу (2) не слід намагатися механічно запам’ятати. Під час множення комплексних чисел треба користуватись відомим правилом множення двочленів a + bί і c + dί з наступною заміною ί²на –1.

Приклади: Виконити множення комплексних чисел.

1) (4-5ί)(3+2ί) = 12+8ί -15ί -10ί²= 12+10-7ί =22-7ί;

2)(Ö3-ί)(Ö2+Ö5ί) = Ö6-Ö2ί+Ö15ί-Ö5 ί²= (Ö6+Ö5) + (Ö15-Ö2)ί;

3)8ίх3ίхÖ3 = -24Ö3;

4)(2-ί)(-5) = -10+5ί;

5)(-4-3ί)(-6ί) = -18+24ί.

Дія множення комплексних чисел підлягає основним законам множення, встановленим для дійсних чисел: переставному і сполучному.

Знайдемо добуток двох спряжених комплексних чисел. Маємо: (a + bί)( a - bί) = a² - (bί)² = a² -b²ί² = a² + b², тобто (a + bί)( a - bί) = a² + b².

Приклади: Обчислити добуток.

1) (3+5ί)(3-5ί) = 9+25 = 34;

2) (2+ί)(2-ί) = 4+1 = 5;

3) (4+Ö3ί)(4-Ö3ί) = 16+3 = 19;

4) (Öх+Öуί)( Öх-Öуί) = х+у;

5) (3/4+2/5ί)(3/4-2/5ί) = 9/16+4/25 = 289/400.

Читаючи рівність (a + bί)( a - bί) = a² + b² справа наліво, робимо висновок, що сумму квадратів будь – яких двох чисел можна подати у вигляді добутку комплексно – спряжених множників.

Приклади: Розкласти на множники двочлени.

1) а+9 = (а+3ί)(а-3ί);

2) 16m²+25n² = (4m+5nί)(4m-5nί);

3) 49+36 = (7+6ί)(7-6ί);

4) а+16 = (Öа+4ί)( Öа-4ί);

5) в+7 = (Öв+Ö7ί)( Öв-Ö7ί).

г) Ділення комплексних чисел.

Ділення комплексних чисел означають як дію, обернену до дії множення, коли за даним добутком і одним з множників знаходять другий, невідомий множник. Причому в множині комплексних чисел залишається вимога, щоб дільник був відмінним від нуля.

Означення. Часткою комплексних чисел z₁ = a + bί та z₂ = c + dί називеється таке комплексне число z₃= x+yί, яке при множенні на z₂ дає z₁.

Можливість ділення комплексних чисел і його однозначність потребує доведення.

Доведемо, що частка комплексних чисел z₁ = a + bί та z₂ = c + dί визначена і до того ж однозначно, якщо c + dί≠ 0+0ί. Отже, доведемо, що за умови існує, і до того ж єдине, комплексне число z₃= x+yί, яке при множенні на z₂ дає z₁. За означенням дії ділення, (c + dί)( x+yί) = a + bί. Виконавши в лівій частині цієї рівності дію множення, дістанемо: (c x - dy) + (cy +d x)ί = a + bί.

З умови рівності двох комплексних чисел випливає:

c x - dy= a

cy +d x=b

Система має єдиний розв’язок:

x= (a c +bd)\( c²+d²);

y = (bc- ad)\( c²+d²).

Із доведення випливає, що ділення ккомплексних чисел відбувається за таким правилом:

(a + bί)\( c + dί) = (a c +bd)\( c²+d²) + (bc- ad)ί\( c²+d²).

Цей результат можна дістати, помноживши ділене і дільник на число, спряжене до дільника. Покажемо це:

(a + bί)\( c + dί) = (a + bί)( c - dί)\( c + dί)( c - dί) = ((a c +bd) + (bc- ad)ί )\( c²+d²) = (a c +bd)\( c²+d² ) + ((bc- ad)ί)\( c²+d²).

Цим принципом користуються під час розв’язування вправ на ділення комплексних чисел.

Приклади. Знайти частку комплексних чисел.

а) (2+5ί)/(3-2ί) = (2+5ί)(3+2ί)/(3-2ί)(3+2ί) = (-4+19ί)/13 = -4/13+19ί/13;

б) (3+ί)/ί = (3+ί)(-ί)/ί = 1-3ί;

д) піднесення комплексних чисел до степеня.

За означенням, ί¹ = ί, ί²= - 1.

Користуючись рівністю ί²= - 1, визначеко кілька послідовних ступенів уявної одиниці:

ί³ =ί²ί= - 1ί= -ί; ί = ί³ί = -ίί= 1; ί=ίί=ί; ί=ίί=-1; ί=ίί=-ί; ί=-ίί=1.

Оскільки ί=1, то значення степенів періодично повторюються із збільшенням показника на 4. Так, ί²= ί =-1, ί³=ί =-ί, ί =ί = 1і так далі.

Означення. Щоб піднести число до степеня з натуральним показником n, треба показник сепеня поділити на 4 і піднести до степеня, показник якого дорівнює остачі від ділення.

Приклади. Піднести до степеня:

а) ί = ί =ί = ίί =-ί ;

б) ί = ί = ί = ί²= -1;

в) ί =ί = ί = -ί.

Правила піднесення до степеня уявної одиниці застосовується при піднесенні до степеня комплексних чисел.

Приклади. Піднести до степеня двочлени:

1) (2+5ί)² = 4+20ί +25ί² = -21+20ί;

2) (3+2)³ = 27+54ί +36ί²+8 = -9+36ί;

3) (1+ί)² = 1+2ί + ί²= 2ί;

4) (1-ί) ² = 1-2ί + ί²= -2ί;

5) (1-ί) = (1-2ί +ί) ² = (-2ί) ² = 4ί² = -4;

6) (1+ί) = ((1+ί)²)³ = (2ί) ³ = 8ί³ = -8 ί;

7) (1-ί) = ((1-ί) ²) = (-2ί) = -32ί = -32ί.

Рівності(1+ί)² = 1+2ί + ί²= 2ί, (1-ί) ² = 1-2ί + ί²= -2ί корисно запам’ятати, бо їх часто використовують.

3. Геометрична інтерпретація комплексних чисел

Вивчаючи комплексні числа, можна використовувати геометричну термінологію і геометричні міркування, яякщо встановити взаємно однозначну відповідність між множиною комплексних чисел і множиною точок координатної площини. Цю відповідність можна встановити так. Кожному комплексному числу a + bί поставимо у відповідність точку М(a;b) координатної площини, тобто точку, абсциса якої дорівнює дійсній частині комплексного числа, а ордината – коефіцієнту уявной частини. Кожній точці М(a;b) координатної площини поставимо у відповідність комплексне число (малюнок 1).

Малюнок 1

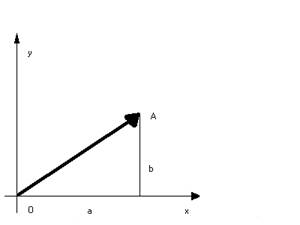
Очевидно, що така відповідність є взаємно однозначною. Вона дає можливість інтерпретувати комплексні числа як точки деякої площини, на якій вібрано систему координат. Координатну площину називають при цьому комплексною, вісь абсцис – дійсною віссю, бо на ній розміщені точки, що відповідають комплексним числам a + 0ί, тобто відповідають дійсним числам. Вісь ординат називають уявною віссю – на ній лежать точки, які відповідають уявним комплексним числам 0+ bί.

Зручною є також інтерпритація комплексного числа як вектора ОМ (дивіться малюнок 2)

Малюнок 2

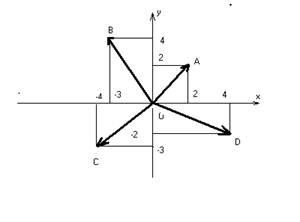
Поставимо у відповідність кожному комплексному числу вектор з початком у точці О(0;0) і кінцем у точці М(a;b). Ви знаєте, що такий вектор називають радіус – вектором, а його проекції на осі є координатами вектора. Отже, можна сказати, що геометрични зображенням комплексного числа z = a + bί є радіус – вектор з координатами a і b. Відповідність між множиною комплексних чисел, з одного боку, і множиною точок або векторів площини, з іншого, дає змогу комплексні числа називати векторами аьо точками і говорити, наприклад, про вектор a + bί або про точку a + bί.

На малюнку 2 вектори ОА, OB, OC, OD є відповідними геометричними зображеннями комплексних чисел z₁= 2+2ί; z ₂= -3+4ί; z ₃= -4-3ί; z ₄= 4-2ί.

Протилежним комплексним числам відповідають протилежні вектори.

Малюнок 3

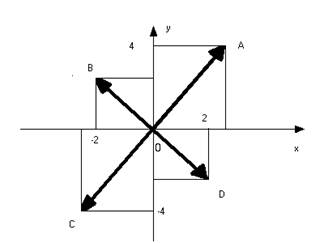
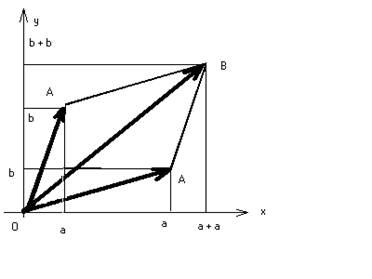
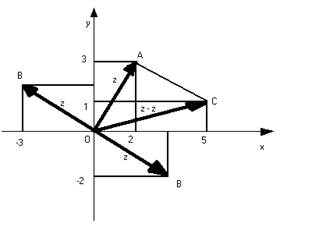
На малюнку 3 зображено дві пари протилежних векторів OA i OC, OB i OD, що відповідають парам протилежних чисел 3+4ί та –3-4ί; -2+3ί та 2-3ί.

Геометричне зображення суми і різниці двох комплексних чисел.

З геометричної інтерпретації комплексних чисел у вигляді векторів випливає можливість геометричного зображення додавання комплексних чисел. Воно знаходиться до знаходження сум двох векторів за відомим правилом паралелограма.

Нехай дано два комплексних числа z₁ = a₁ + b₁ί та z₂ = a₂ + b₂ί, яким відповідають радіус – вектори ОА і ОА (малюнок 4). Побудуємо на цих векторах як на сторонах паралелограм. Тоді зображенням суми комплексних чисел z₁ і z₂ буде вектор ОВ (діагональ паралелограма) справді, при додаванні векторів їх відповідні координати додають. Тому, якщо вектор ОА₁ має координати (a₁;b₁), а вектор ОА₂ (а₂;b₂), то їх сума – вектор ОВ – матике координати (а₁+а₂;b₁+b₂). Вектор ОВ відповідає комплексному числу (а₁+а₂) + (b₁+b₂), яке є сумою чисел z₁ і z₂.

Малюнок 4

Нехай, наприклад, треба знайти геометричне зображення різниці z₁ - z₂ комплексних чисел z₁ = 2+3ί та z₂ = -3+2ί. Будуємо вектор ОА, що є зображенням числа z₁, і додаємо до нього вектор ОВ, який зображує число z₂ = -3+2ί, протилежне від’ємнику (малюнок 5). Шукану різницю зображують вектором ОС, що є сумою векторів ОА і ОВ. Йому відповідає комплексне число 5+ί.

Малюнок 5

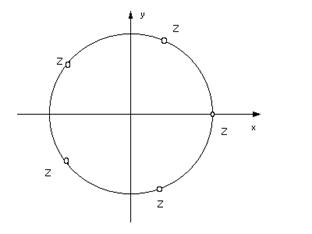
4. Тригонометрична форма запису комплексних чисел

Запис числа z у вигляді a + bί називається алгебраїчною формою запису комплексного числа. Крім алгебраїчної форми використовують й інші форми запису комплексних чисел – тригонометрична і показникова. Розглянемо тригонометричну форму запису, а для цього введемо поняття про модуль і аргумент комплексного числа.

а) Модуль комплексного числа.

Побудуємо радіус – вектор ОА, що є геометричним образом комплексного числа z = a + bί (малюнок 6).

Модулем комплексного числа z = a + bί називається значення Öa² + b². Число r =Ö a² + b² перетворюється на нуль тільки за умов a =0, b =0.

Модуль комплексного числа a + bί позначається символом a + bί. Отже, a + bί = Ö a² + b².

Якщо комплексні числа мають один і той самий модуль, то кінці векторів, які зображують ці числа, лежать на колі з центром у початку координат і радіусом, що дорівнює їх модулю.

Приклади: знайти модулі даних комплексних чисел.

1) 5+7ί = Ö25+49 = Ö74;

2) –2-3ί = Ö4+9 = Ö13;

3) 8+0ί=Ö64 = 8;

4) 5ί= 5.

Б) аргумент комплесного числа.

Нехай радіус – вектор ОА зображує комплексне число z = a + bί (дивіться малюнок 6). Позначимо α кут, який утворює вектор ОА з додатним напрямом осі х. Числове значення кута α, виміряного в радіанах, називається аргументом комплексного числа a + bί. Якщо комплексне число дорівнює нулю, то вектор ОА перетворюється в точку (нуль – вектор), і говорити про його напрям немає сенсу. Тому вважають, що число нуль не має аргументу. Кожне відмінне від нуля комплексне число має нескінченну множину значень аргументу, які відрізняються один від одного на ціле число повних обертів, тобто на величину 2πn, де n – довільне ціле число. Значення аргументу, взяте в межах першого кола, тобто від 0 до 2π, називається головним. Головне значення аргументу комплексного числа можна визначити з рівності tg α = b/a. Справді, за знаками a i b можна встановити, в якій четверті міститься кут α, і за величиною tg α, використовуючи таблиці, знайти величину кута α.

Приклади: знайти головне значення аргументу даних комплексних чисел.

1) z = 1+ί;

Маємо: tg α = 1. Оскільки a = 1 та b = 1, радіус – вектор, який відповідає даному комплексному числу, належить І чверті і тому α - гострий кут. Отже, = π/4.

2) z = -2+2Ö3ί;

Маємо: tg α = 2Ö3/(-2) = -3. Тут а = -2, b = 2Ö3, тобто радіус – вектор, який відповідає даному комплексному числу, належить ІІ чверті. Отже, α = π 2/3.

3) z = -1-ί;

Маємо: tg α = 1. Радіус – вектор, що відровідає даному комплексному числу, належить ІІІ чверті. Отже, α = π 5/4.

4) z = 1-Ö3ί;

Маємо: tg α = -Ö3. Тут а = 1, b = -Ö3. Радіус – вектор, що відповідає даному комплексному числу, належить IV чверті. Отже, = π 5/3.

в) тригонометрична форма комплексного числа.

Нехай вектор ОА є геометричним зображенням комплексного числа z = a + bί (дивіться малюнок 7), модуль якого дорівнює r, а аргумент α. У прямокутному трикутнику АОС а = r cos α, d = r sin α. Підставляючи у запис комплексного числа замість а та d їхні значення, виражені через модуль і аргумент, дістанемо :

Z = r cos α + ίr sin αί = r(cos α + ίsin α).

Вираз r(cos α + sin αί) називається тригонометричною формою комплексного числа. Будь – яке число a + bί, дане в алгебраїчній формі, можна подати в тригонометричній формі. Модуль r знаходимо за формулою r =Ö a² + b², а кут α визначаємо із залежності tg α =b\a, яка випливає з формул cos α = a\r, sin α = b\r.

Приклади:

а) z = -1-Ö3ί;

Маємо: r = Ö(-1)²+(- Ö3)² = 2; tg α = Ö3; α = 4π\3 + πn, n є Z.

Через те, що радіус – вектор, який зображує число z = a + bί, розміщений у ІІІ чверті комплексної площини, то за аргумент беремо α = 4π\3 + πn. Отже, -1-Ö3ί = 2(соs 4π\3 + ί Sin 4π\3).

б) z = ί;

Тут а = 0, b = 1, отже, r = 1. Вектор, що зображує число ί, утворює з віссю абсцисс кут π\2 (поясніть чому). Отже, ί = cos π\2 + ί sin π\2.

в) z = 3.

Тут а = 3, b = 0, отже, r = 3.

3 = 3(cos 0 + ί sin 0).

Розглянемо приклади переходи від тригонометричної форми комплексного числа до алгебраїчної.

Приклади:

а) 2(cos π\3+ ί sin π\3) = 2(1\2+Ö3ί \2) = 1 +Ö3ί;

б) 4(cos 2π\3 + ί sin 2π\3) = 4(-1\2+Ö3ί \2) = -2 + 2Ö3ί.

г) Множення і ділення комплексних чисел, записаних в тригонометричній формі.

Тригонометрична форма запису комплексних чисел виявляється дуже зручною під час множення і ділення чисел. Нехай Z₁=r₁(cos α₁ + ί sin α₁), Z₂=r₂(cos α₂ + ί sin α₂) – два числа, що записані в тригонометричній формі. Тоді

Z₁ Z₂= r₁r₂( cos α₁ cos α₂ - sin α₁ sin α₂ + ί sin α₁cos α₂ + ί sin α₂ cos α₁), або Z₁ Z₂= r₁r₂( cos (α₁ + α₂) + ί sin (α₁ + α₂)).

Отже, справедливим є твердження: під час множення комплексних чисел у тригонометричній формі модулі їх перемножуються, а аргументи додаються. Для знаходження частки множимо чисельник і знаменник на число, спряжене до знаменника:

Z₁\Z₂=r₁(cos α₁ + ί sin α₁)(cos α₂ - ί sin α₂)\ r₂(cos α₂ + ί sin α₂)(cos α₂ - ί sin α₂) = r₁\r₂х(cos (α₁ - α₂) + ί sin (α₁ - α₂))\( cos² α₂ + ί sin ²α₂)= r₁( cos (α₁ - α₂) + ί sin (α₁ - α₂))\r₂.

Отже, під час ділення комплексних чисел їх модулі діляться, а аргументи віднімаюьтся.

Приклади. Виконати множення і ділення комплексних чисел, записаних у тригонометричній формі.

а) Z₁=3(cos 7° + ί sin 7°); Z₂=8(cos 15° + ί sin 15°);

д) Подаємо без доведення правила піднесення до степеня комплексного числа, записаного в тригонометричній формі.

При будь – якому натуральному n

(cos α + ί sin α)ⁿ = cos nα + ί sin nα.

Це твердження називається формулою Муавра.

Приклади. Виконати дії піднесення до ступеня даного комплексного числа.

Z=Ö3-ί. Обчислити Z.

Модуль даного числа дорівнює Ö(Ö3)²+1 = 2, аргумент α = -π\6, отже модуль числа Z дорівнює 2, аргумент 9α = -9π\6 = -3π\2. Таким чином,

(Ö3-ί) = 2 (cos (-3π\2)+ ί sin(-3π\2)) = 512ί.

є) добування кореня з комплексного числа.

Корінь n – го ступеня з числа Z=r(cos α + ί sin α) обчислюють за формулою

ω = Ör(cos ((α + 2 πк)\n) + ί sin ((α + 2 πк)\n)),

де к – деяке ціле число (к є Z).

Підставляючи замість к значення 0, 1, 2…n – 1, дістанемо n різних значень кореня. Так, якщо n = 2, к = 2 матимемо sin ((α + 4 π) = sin α\2 і так далі.

Приклади. Знайти всі значення Ö1

Оскільки 1 = 1(cos 0 + ί sin 0), то

Ö1(cos 0 + ί sin 0) = 1(cos ((0 + 2 πк)\5) + ί sin ((0 + 2 πк)\5), к = 0, 1, 2, 3, 4. Надаючи к послідовно значень 0, 1, 2, 3, 4, выдповыдно дыстанемо:

Z₁= 1, якщо к = 0;

Z₂= cos 2π\5 + ί sin 2π\5, якщо к = 1;

Z₃= cos 4π\5 + ί sin 4π\5, якщо к = 2;

Z₄= cos 6π\5 + ί sin 6π\5, якщо к = 3;

Z₅= cos 8π\5 + ί sin 8π\5, якщо к = 4.

Цікавий такий факт. Модулі всіх цих значень Ö1 дорівнюють 1. Отже, точки Z₁, Z₂, Z₃, Z₄, Z₅ лежать на колі радіуса 1 з центром у початку координат. Побудувавши аргументи значень Z₁, Z₂, Z₃, Z₄, Z₅ , помітимо, що точки, які зображують числа Z₁, Z₂, Z₃, Z₄, Z₅, є вершинами правильного п’ятикутника (малюнок 7).

Взагалі точки, які відповідають значенням кореня n – го ступеня з комплексного числа Z=r(cos α + ί sin α), розміщуються у вершинах правильного n – кутника з центром у точці О.

Малюнок 7

Література

1. Пискунов Н. С. Дифференциальное и интегральное исчисление для ВТУЗов. Т. 1 М.: 1968.

2. Воробьева Г. Н., Данилова А. Н. Практикум по численным методам. М.: 1979.

3. Математический практикум. М.: 1960.