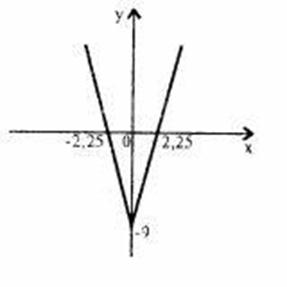
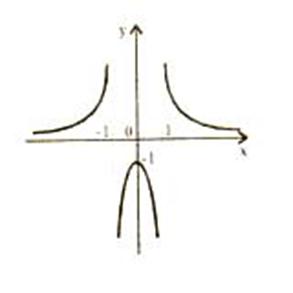
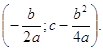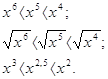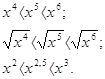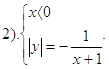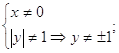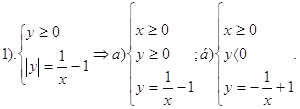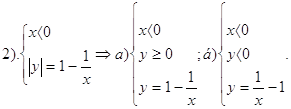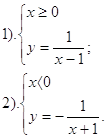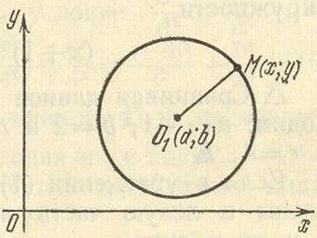|
Рефератыкосмонавтике административному праву хозяйственному праву устройствам экологическому праву криминалогия гражданский и землепользование обществознание |
Реферат: Графики и их функцииРеферат: Графики и их функцииМинистерство образования Российской Федерации Муниципальное общеобразовательное учреждение “Средняя общеобразовательная школа №22” Графики и их функции Выполнили: Ученики 9 "Б" класса Кузнецов Евгений и Руди Алексей Руководитель: Зенина Алевтина Дмитриевна, преподаватель математики Тюмень, 2006 ОглавлениеВведение. 4 Глава I. История возникновения. 5 1.1 Возникновение и понятие функции в древнем мире. 5 1.2 Возникновение и понятие функции в древнем Египте. 5 1.3 Возникновение и понятие функции в Древнем Вавилоне. 6 1.4 Возникновение и понятие функции в Древней Греции. 6 1.5 Графическое изображение зависимостей, история возникновения. 7 1.6 Вклад в развитие графиков функций Рене Декартом.. 8 Глава II. Определение функций. 9 2.1 Основные понятия о функциях. 9 2.2 Способы задания функций. 10 Глава III. Исследования функций и их графиков. 12 3.1 Простейшие функции и их графики. 12 3.2 Тригонометрические функции. 18 3.3 Кривые второго порядка. 19 Глава IV. Методы построения графиков функций. 23 4.1 Параллельный перенос. 23 4.1.1 Перенос вдоль оси ординат. 23 4.1.2 Перенос вдоль оси абсцисс. 24 4.2 Отражение. 24 4.2.1 Построение графика функции вида y = f(-x) 24 4.2.2 Построение графика функции вида y = - f(x) 25 4.2.3 Построение графиков четной и нечетной функций. 25 4.2.4 Построение графика обратной функции. 26 4.3 Деформация. 26 4.3.1 Деформация графика вдоль оси ординат. 26 4.3.2 Деформация графика вдоль оси абсцисс. 27 4.4 Алгебраические операции над графиками функций. 27 4.4.1 График суммы (разности) функций. 28 4.4.2 График произведения функций. 28 4.4.3 График функции вида. 28 4.4.4 График частного двух функций. 29 4.5 Построение графиков сложных функций. 29 4.5.1 График функции у = [f(x)] k. 29 4.5.2 График функции у = af(x) 30 Глава V: Графики нетрадиционных функций. 31 Заключение. 37 Список литературы.. 39 Приложение 1. 40 Приложение 2. 41 Приложение 3. 42 Приложение 4. 43 Приложение 5. 44 Приложение 6. 45 Приложение 7. 46 Приложение 8. 47 Приложение 9. 48 Приложение 10. 49 Приложение 11. 50 Приложение 12. 51 Приложение 13. 52 Приложение 15. 54 ВведениеИзучение поведения функций и построение их графиков является важным разделом математики. Свободное владение техникой построения графиков часто помогает решить многие задачи и парой является единственным средством их решения. Кроме того, умение строить графики функций представляет большой самостоятельный интерес. Цели реферата - систематизация методов построения графиков функций выходящих за рамки знаний предусмотренных средней школой. Так же в этом реферате хотелось бы отобразить методы и виды решения различных графиков функций. Основные положения по этим не традиционным графиком будут изложены в главе VI. При этом главное внимание уделено именно методам построения графиков, а не изучению их видов функций. Задачи: систематизация старых знаний наработка новых способов построения графиков функций изучение новых графиков функций Объект исследования - алгебра. Предмет исследования - графики и их функции. Материал, связанный с построением графиков функций, в средней школе изучается недостаточно полно с точки зрения требований предъявленных на экзаменах. Поэтому задачи на построение графиков не редко вызывают затруднение у поступающих. Основываясь на этом факте, эта тема является необходимой для подробного рассмотрения. В основном для этого реферата использовались математические справочники и специальная литература. Глава I. История возникновения1.1 Возникновение и понятие функции в древнем миреПонятие функции уходит своими корнями в ту далекую эпоху, когда люди впервые поняли, что окружающие их явления взаимосвязаны. Они еще не умели считать, но уже знали, что, чем больше оленей удастся убить на охоте, тем дольше племя будет избавлено от голода, чем дольше горит костер, тем теплее будет в пещере. С развитием скотоводства и земледелия, ремесла и обмена увеличилось количество известных людям зависимостей между величинами. Многие из них выражались с помощью чисел. Это позволило формулировать их словами "больше на", "меньше на", "больше во столько-то раз". Если за одного быка давали 6 овец, то двух быков обменивали на 12 овец, а трех быков на 18 овец. Такие расчеты привели к возникновению понятия о пропорциональности величин. 1.2 Возникновение и понятие функции в древнем ЕгиптеНо когда возникли первые цивилизации, образовались большие (по тогдашним масштабам), армии, началось строительство гигантских пирамид, то понадобились писцы, которые учитывали поступающие налоги, определяли количество кирпичей, потребное для возведения дворцов, подсчитывали, сколько продовольствия надо заготовить для дальних походов. От одного поколения писцов к другому переходили правила решения задач, чтобы решить такие задачи, надо было знать, как зависят объемы геометрических фигур от их размеров, уметь учитывать наклон насыпи. Некоторые египетские задачи показывают, что в то время умели даже вычислить объем пирамиды 1.3 Возникновение и понятие функции в Древнем ВавилонеВысокого уровня достигла математика в Древнем Вавилоне. Чтобы облегчить вычисления, вавилоняне составили таблицы обратных значений чисел, таблицы квадратов и кубов чисел и даже таблицы для суммы квадратов чисел их кубов. Говоря современным языком, это было табличное задание функций y = 1/x, y = x2, y = x3, y = x2 + x3 Пользуясь такими таблицами, вавилоняне могли решать и
обратные задачи - по заданному объему куба находить длину его стороны, т.е. Извлекать
кубические корни. Они умели даже решать уравнения вида x2 + x3 = a. Были у
вавилонян и таблицы функций двух переменных, например таблицы сложения и
умножения. Пользуясь различными таблицами, они могли вычислить и длину
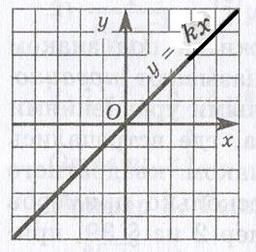
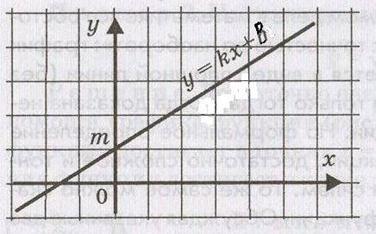
гипотенузы по длинам катетов, т.е. Находить значение функции Разумеется, путь от появления таблиц до создания общего понятия функциональной зависимости был еще очень долог, но первые шаги по этому пути уже были сделаны. 1.4 Возникновение и понятие функции в Древней ГрецииВ Древней Греции наука приняла иной характер, чем в Египте и в Вавилоне. Появились профессиональные ученые, которые изучали саму математическую науку, занимались строгими логическими выводами одних утверждений из других. Многое из того, что делали древнегреческие математики, тоже могло привести к возникновению понятия о функции. Они решали задачи на построение и смотрели, при каких значениях задача имеет решение, изучали, сколько решений может иметь эта задача, и т.д. Древние греки нашли много различных кривых, неизвестных писцам Египта и Вавилона, изучали зависимости между отрезками диаметров и хорд в круге, эллипсе и других линиях. Но все же древнегреческие математики не создали общего понятия функции. 1.5 Графическое изображение зависимостей, история возникновенияИсследование общих зависимостей началось в 14 веке. Средневековая наука была схоластической. Для доказательства своей правоты ученые прибегли не к опыту, а к цитатам из Аристотеля и Платона или к ссылкам на библейские сказания. При таком характере "научных дискуссий" не оставалось места изучению количественных зависимостей, речь шла лишь о качествах предметов и их связях друг с другом. Но среди схоластов возникла школа, утверждавшая, что качества могут быть более или менее интенсивными (платье человека, свалившегося в реку, мокрее, чем у того, кто лишь попал под дождь) Французский ученый Николай Оресм стал изображать интенсивность длинами отрезков. Когда он располагал эти отрезки перпендикулярно некоторой прямой, их концы образовывали линию, названную им "линией интенсивностей" или "линией верхнего края". Современный читатель сразу узнает в ней график соответствующей функциональной зависимости. Оресм изучал даже "плоскостные" и "телесные" качества, т.е. функции, зависящие от двух или трех переменных. Важным достижением Оресма была попытка классифицировать получившиеся графики. Он выделил три типа качеств: Равномерные (с постоянной интенсивностью), равномерно-неравномерные (с постоянной скоростью изменения интенсивности) и неравномерно-неравномерные (все остальные), а также характерные свойства графиков таких качеств. Идеи Оресма на много обогнали тогдашний уровень науки. Чтобы развивать их дальше, нужно было уметь выражать зависимости между величинами не только графически, но и с помощью формул, а буквенной, алгебры в то время не существовало. Лишь после того, как в течение 16 века была постепенно создана буквенная алгебра, удалось сделать следующий шаг в развитии понятия функции. 1.6 Вклад в развитие графиков функций Рене ДекартомЧтобы создать математический аппарат для изучения графиков функций, понадобилось понятие переменной величины. Это понятие было введено в науку французским философом и математиком Рене Декартом (1596-1650). Именно Декарт пришел к идеям о единстве алгебры и геометрии и о роли переменных величин, он разрушил пропасть, лежавшую со времен древнегреческой математики, между геометрией и арифметикой. Чтобы освободить алгебру от несвойственного ей геометрического языка, Декарт ввел фиксированный единичный отрезок и стал рассматривать отношения других отрезков к нему. При записи зависимостей между величинами Декарт стал применять буквы. При этом операциями над величинами соответствовали операции над буквами. Теперь уже для преобразования одной зависимости в другую не надо было писать громоздких пропорций, изучать подобные треугольники и преобразовывать геометрические фигуры. Достаточно было по твердо, установленным правилам делать алгебраические преобразования, причем все эти преобразования производились в общем, виде. Таким образом, графики функций за все время своего существования прошли через ряд фундаментальных преобразований, приведших их к тому виду, к которому мы привыкли. Каждый этап или ступень развития графиков функций - неотъемлемая часть истории современной алгебры и геометрии. Глава II. Определение функций2.1 Основные понятия о функцияхВеличины, участвующие в одном и том же явлении, могут быть взаимосвязаны, так что изменение одних из них влечёт за собой соответствующее изменение других. Например, увеличение (или уменьшение) радиуса круга ведёт к обязательному увеличению (или уменьшению) его площади. В таких случаях говорят, что между переменными величинами существует функциональная зависимость, причём одну величину называют функцией, или зависимой переменной (её часто обозначают буквой у), а другую - аргументом, или независимой переменной (её обозначают буквой х). Функциональную зависимость между х и у принято обозначать символом y=f(x). Если значению х соответствует больше, чем одно значение у. то такая функция называется многозначной. Исследование многозначных функций обычно сводится к исследованию однозначных. Переменная величина у есть функция аргумента х, т.е. y=f(x), если каждому возможному значению х соответствует одно определённое значение у. Графиком функции называется совокупность всех точек на плоскости, прямоугольные координаты которых х и у удовлетворяют уравнению y=f(x). Горизонтальную ось Ох называют осью абсцисс, вертикальную ось Оу - осью ординат. Графическое изображение функции имеет важное значение для её изучения. На графике функции часто непосредственно видны такие её особенности, которые можно было бы установить лишь путём длительных вычислений. Если между величинами х и у существует функциональная связь, то безразлично, какую из этих величин считать аргументом, а какую - функцией. 2.2 Способы задания функцийФункциональная зависимость, устанавливающая соответствие между значениями аргумента х и функции у, может быть различными способами: 1). Табличный способ. При этом способе ряд отдельных значений аргумента х1, х2, …, хk и соответствующий ему ряд отдельных значений функции у1, у2, …, уk задаются в виде таблицы. Несмотря на простоту, такой способ задания функции обладает существенным недостатком, так как не дает полного представления о характере функциональной зависимости между х и у и не является наглядным. 2). Словесный способ. Обычно этот способ задания иллюстрируют примером функции Дирихле у = D (х): если х - рациональное число, то значение функции D (х) равно 1, а если число х - иррациональное, то значение функции D (х) равно нулю. Таким образом, чтобы найти значение D (x0) при заданном значении х = х0, необходимо каким - либо способом установить, рационально или иррационально число х0. 3). Графический способ. Функциональная зависимость может быть задана с помощью графика функции у = f (x). Преимуществом такого способа задания является наглядность, позволяющая установить важные черты поведения функции. Недостаток графического способа заключается в невозможности применения математического аппарата для более детального исследования функции. 4). Аналитический способ. При аналитическом способе задания известна формула, по которой по заданному значению аргумента х можно найти соответствующее значение функции у. В математике чаще всего используется именно аналитический способ задания функций. Преимуществами такого способа задания являются компактность, возможность подсчета значения у при любом значении х и возможность применения математического аппарата для более детального исследования поведения функции. Однако аналитическому способу задания функции присуща недостаточная наглядность и возможная трудность вычисления значений функции. Краткое рассмотрение различных способов задания функции показывает, что для подробного изучения ее поведения лучше всего сочетать исследование аналитического выражения функции с построением ее графика. Наконец, еще раз подчеркнем следующее: из определения функции вытекает, что для ее задания необходимо лишь указать закон соответствия между величинами х и у. Способ же задания этого закона не имеет значения. Глава III. Исследования функций и их графиков3.1 Простейшие функции и их графикиПропорциональные величины. Если переменные величины у и х (прямо) пропорциональны, то функциональная зависимость между ними выражается уравнением y = kx, где k есть некоторая постоянная величина (коэффициент пропорциональности). График прямой пропорциональности есть прямая линия (см. приложение 1), проходящая через начало координат и образующая с осью абсцисс угол α, тангенс, которого равен постоянной k; tg α = k. Поэтому коэффициент пропорциональности k называется также угловым коэффициентом. Линейная функция. Линейной называется функция вида: y = kx + b, в аналитическое выражение, которой переменные х и у входят в первой степени. График линейной функции представляет прямую линию (см. приложение 2), располагающеюся относительно координатных осей различным образом, в зависимости от постоянных коэффициентов, k и b, которые могут принимать положительные или отрицательные значения или быть равным нулю. Для построения графика линейной функции можно воспользоваться геометрическим смыслом коэффициентов k и b или найти две точки прямой на плоскости, например, точки пересечения с осями координат. Свойства функции y = kx+b: D(f) =
(- Возрастает, если k >0, убывает, если k<0; Не ограничена ни сверху, ни снизу; Нет ни наибольшего, ни наименьшего значений; Функция непрерывна; E(f) =
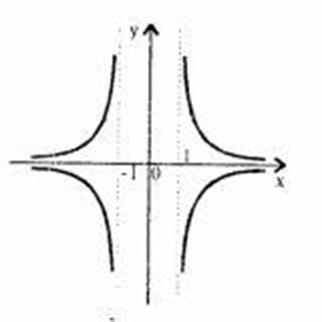
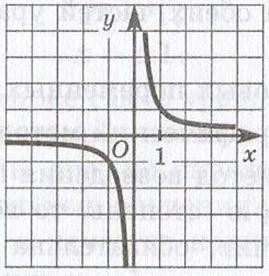
(- Обратная пропорциональность. Если переменные величины
у и х обратно пропорциональны, то функциональная зависимость между ними
выражается уравнением Свойства функции D(f) =
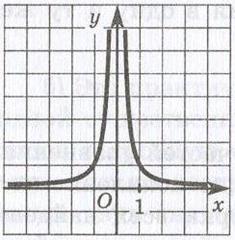
(- Если с >0, то функция убывает на открытом луче (- Не ограничена ни снизу, ни сверху; Нет ни наименьшего, ни наибольшего значений; Функция непрерывна на открытом луче (- Е(f) = (- Если с>0, то функция выпукла вверх при х<0, т.е.
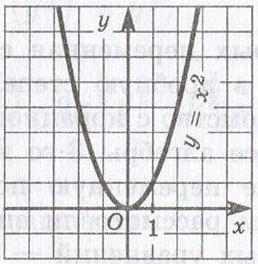
на отрытом луче (- Функция имеет асимптоты y = 0 и x = 0/ Квадратичная функция. Функция y = ax2 + bx + с (a, b,
с - постоянные величины; а ≠ 0) называется квадратичной. В простейшем
случае y = ax2 (b = с = 0) график есть кривая линия, проходящая через начало
координат. Кривая, служащая графиком функции y = ax2, есть парабола (см. приложение
4). Каждая такая парабола имеет ось симметрии (OY), называемую осью параболы. Точка
О пересечения параболы с ее осью называется вершиной параболы. График функции y
= ax2 + bx + с имеет ту же формулу, что и график функции y = ax2 (при том же
значении а), т.е. также есть парабола. Ось этой параболы по-прежнему вертикальна,
но вершина лежит не в начале координат, а в точке Свойства функции ax2 + bx + с: Для случая, а>0 D(f) =
(- Убывает на луче Ограничена снизу, не ограничена сверху; унаим. = y0, yнаиб. Не существует; Непрерывна;
Выпукла вниз. Для случая, а<0 D(f) =
(- Убывает на луче Не ограничена снизу, ограничена сверху;
Непрерывна; 6. Выпукла вверх. Свойства функции y = ax2: Для случая, а>0 D(f) =
(- Убывает на луче Ограничена снизу, не ограничена сверху; унаим. = 0, yнаиб. Не существует; Непрерывна; E(f) = Выпукла вниз. Для случая, а<0 D(f) =
(- Убывает на луче Не ограничена снизу, ограничена сверху; унаим. Не существует, yнаиб. = 0; Непрерывна; E(f) = Выпукла вверх. Степенная функция. Обычно степенными функциями
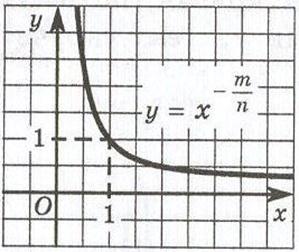
называют функции вида График степенной функции y = xn в случае четного n (n = 4, 6,8, …) похож на параболу, а график степенной функции y = xn в случае нечетного n (n = 5, 7, 9, …) похож на кубическую параболу. Если r = - n, то получаем функцию y = x - n, т.е.
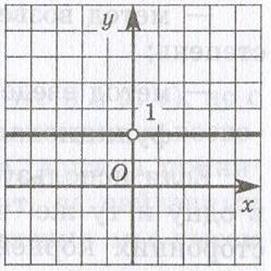
Наконец, если r = 0, т.е. речь идет о функции y = x0, то в результате получается обыкновенная функция у = 1, где х ≠ 0; график этой функции изображен (см приложение 6). Теперь рассмотрим функцию y = xr,
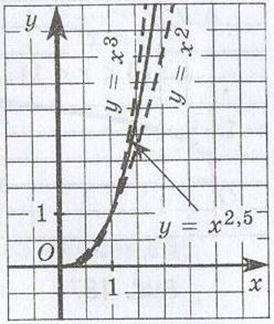
где r - положительное или отрицательное дробное число. Рассмотрим в
качестве примера функцию y = x2,5. Область ее определения - луч 1) кубическая парабола располагается ниже, а на открытом луче (1; +∞) выше параболы. Нетрудно убедиться в том, что график функции у = х2,5 проходит через точки (0; 0) и (1; 1), как и графики функций у = х2, у = х3. При остальных значениях аргумента х график функции у = х2,5 находится между графиками функций у = х2 и у = х3 (см. приложение 7). Почему так происходит? Посмотрим: 1). Если 0 < х < 1, то 2). Если х > 1, то
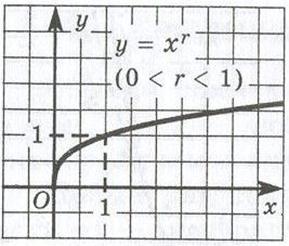
Примерно так же обстоит дело для любой степенной
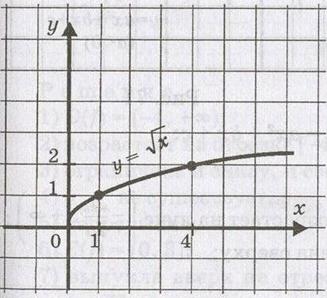
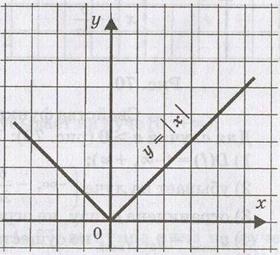
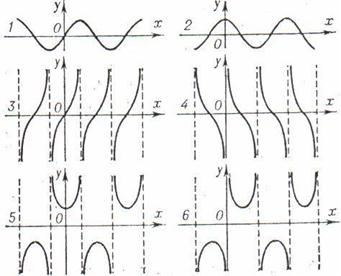
функции вида у = хr, где Свойства функции D(f) = не является ни четной, ни нечетной; возрастает на не ограничена сверху, ограничена снизу; не имеет наибольшего значения; у наим. = 0; непрерывна; E(f) = выпукла вниз. Рассмотрим степенную функцию Свойства функции D(f) = не является ни четной, ни нечетной; возрастает на не ограничена сверху, ограничена снизу; не имеет наибольшего значения; у наим. = 0; непрерывна; E(f) = выпукла вверх. Нам осталось рассмотреть степенную функцию вида Свойства функции D(f) = не является ни четной, ни нечетной; возрастает на не ограничена сверху, ограничена снизу; не имеет ни наибольшего значения, ни наименьшего значения; непрерывна; E(f) = выпукла вниз. Функция Свойства функции D(f) = Возрастает; Ограничена снизу, не ограничена сверху; у наим. = 0, yнаиб. = Не существует; Непрерывна; E(f) = Выпукла вверх. 7. Функция у = - х, х≤0 (см. приложение 11). Свойства функции D(f) =
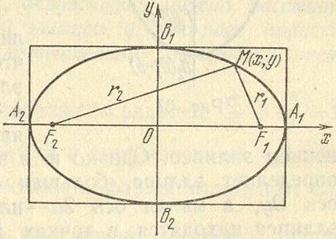
(- Убывает на луче Ограничена снизу, не ограничена сверху; унаим. = 0, yнаиб. Не существует; Непрерывна; E(f) = Выпукла вниз. 3.2 Тригонометрические функцииПо причине того, что тригонометрические функции изучаются в школьной программе, в реферате на них уделено минимум внимания. Все основные положения указанны в таблице (см. приложение 12), а их графики приведены далее (см. приложение 13). 3.3 Кривые второго порядкаВ предыдущем параграфе было установлено, что всякая прямая в прямоугольной системе координат Оху определяется уравнением первой степени относительно переменных х и у. Так же было установлено, всякое уравнение первой степени ах + bу + с = 0 в прямоугольной системе координат определяет прямую и притом единственную, если а² + b² ¹ 0. В настоящей главе мы займемся изучением линий определяемых уравнениями второй степени относительно текущих координат х и у: ах² + 2bху + су² + 2dх + 2eу + f = 0 (1) Такие линии называют линиями (кривыми) второго порядка. Коэффициенты уравнения (1) могут принимать различные действительные значения, исключая одновременное равенство а, b и c нулю (в противном случае уравнение (1) не будет уравнением второй степени). Эллипс. Эллипсом называют множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами. Составим уравнение эллипса с фокусами в данных точках F1 и F2. Для этого выберем прямоугольную систему координат так, чтобы ось Ох проходила через фокусы, а начало координат делило отрезок F1F2 пополам (см. приложение 14). Обозначив F1F2 = 2с, получим F1(с; 0) и F2(-с; 0). Пусть М(х; у) - произвольная точка эллипса. Расстояние r1 = F1M и r2 = F2M называются фокальными радиусами точки М. Положим r1 + r2 = 2а; (1) Тогда согласно определению эллипса 2а - величина постоянная, причем 2а>2с, т.е. а>c. По формуле расстояния между двумя точками находим r1 = Подставим найденные значения r1 и r2 в равенство (1) получим уравнение эллипса
После несложных преобразований уравнение примет вид
Уравнение (2) называется каноническим уравнением эллипса. Исследование: Координаты точки О(0; 0) не удовлетворяют уравнению (2), поэтому эллипс, определяемый этим уравнением, не проходит через начало координат. Найдем точки пересечения эллипса с осями координат. Положив в уравнении (2) у = 0, найдем х = ± а. Следовательно, эллипс пересекает ось Ох в точках А1(а; 0) и А2(-а; 0). Аналогично получаем точки пересечения эллипса с осью Оу: В1(0; b) и B2(0; - b) D(y) Î [-a; a] E(y) Î [-b; b] При возрастании ½х½ от 0 до а величина ½у½ убывает от b до 0, а при возрастании ½у½от 0 до b величина ½х½ убывает от а до 0. Частным случаем эллипса является окружность, где а = b. Окружность Как известно, окружностью называют множество всех точек плоскости, одинаково удаленных от данной точки, называемой центром. Пусть дана окружность радиусом r с центром в точке О1(a; b) (см. приложение 15); требуется составить ее уравнение. Возьмем на данной окружности произвольную точку М (х; у) Имеем: О1М = r, т.е. Откуда (х-а) ² + (у - b) ² = r² (1) Итак, уравнению (1) удовлетворяют координаты произвольной точки окружности. Более того, этому уравнению не удовлетворяют координаты никакой точки, не лежащей на окружности, так как если О1М< r, то (х-а) ² + (у - b) ² < r², и если О1М> r, то (х-а) ² + (у - b) ² > r². Следовательно, (1) Есть уравнение окружности радиусом r с центром в точке О1(a; b). Если центр окружности находится на оси Ох, т.е. если b = 0, то уравнение (1) примет вид (х-а) ² + у² = r² Если центр окружности находится на оси Ох, т.е. если b = 0, то уравнение (1) примет вид х² + (у - b) ² = r² Наконец, если центр окружности находится в начале координат, т.е. если а = b = 0, то уравнение примет (1) вид х² + у² = r² Если в уравнении (1) раскрыть скобки, перенести все члены в левую часть и расположить их по степеням х и у, то получим x² + y² - 2ax - 2by + a² + b² - r² = 0 Отсюда следует, что уравнение окружности является уравнением второй степени относительно переменных х и у, как бы она ни была расположена в плоскости Оху. В этой главе были рассмотрены основные простейшие функции, кривые второго порядка и тригонометрические функции, так же представлены их графики. Глава IV. Методы построения графиков функцийИсследование функции дает возможность найти область определения и область изменения функции, области ее убывания или возрастания, асимптоты, интервал знакопостоянства и др. Однако при рассмотрении графиков многих функций часто можно избежать проведения подобного исследования, используя ряд методов, упрощающих аналитическое выражение функции и облегчающих построение графика. Изложению именно таких методов посвящается эта глава, которая может служить практическим руководством при построении многих функций. 4.1 Параллельный перенос4.1.1 Перенос вдоль оси ординатf(x) => f(x) - b Пусть требуется построить график функции у = f(х) - b. Нетрудно заметить, что ординаты этого графика для всех значений x на ½b½ единиц меньше соответствующих ординат графика функций у = f(х) при b>0 и на ½b½ единиц больше - при b<0. Следовательно, график функции у = y(х) - b можно получить параллельным переносом вдоль оси ординат графика функции у = f(х) на ½b½единиц вниз при b>0 или вверх при b<0. Перемещение графика связано с его перерисовыванием, что бывает затруднительно, особенно в случае сложных графиков. Перенос же графика на ½b½единиц вниз или вверх вдоль оси ординат эквивалентен соответствующему противоположному переносу оси абсцисс настолько же единиц. Именно этим способом мы будем пользоваться. Тогда представив исходную функцию в виде у + b = f(х), сформулируем следующее правило. Для построения графика функции y + b = f(x) следует построить график функции y = f(x) и перенести ось абсцисс на ½b½ единиц вверх при b>0 или на½b½ единиц вниз при b<0. Полученный в новой системе координат график является графиком функции y = f(x) - b. 4.1.2 Перенос вдоль оси абсциссf(x) => f(x + a) Пусть требуется построить график функции у = f(x + a). Рассмотрим функцию y = f(x), которая в некоторой точке x = x1 принимает значение у1 = f(x1). Очевидно, функция у = f(x + a) примет такое же значение в точке x2, координата которой определяется из равенства x2 + a = x1, т.е. x2 = x1 - a, причем рассматриваемое равенство справедливо для совокупности всех значений из области определения функции. Следовательно, график функции у = f(x + a) может быть получен параллельным перемещением графика функции y = f(x) вдоль оси абсцисс влево на½a½ единиц при a>0 или вправо на ½a½ единиц при a<0. Параллельное же перемещение вдоль оси абсцисс на ½a½ единиц эквивалентно переносу оси ординат на столько же единиц, но в противоположную сторону. Таким образом, получаем следующее правило. Для построения графика функции y = f(x + a) следует построить график функции y = f(x) и перенести ось ординат на ½a½ единиц вправо при a>0 или на½a½ единиц влево при a<0. Полученный в новой системе координат график является графиком функции y = f(x + a). 4.2 Отражение4.2.1 Построение графика функции вида y = f(-x)f(x) => f(-x) Очевидно, что функции y = f(-x) и y = f(x) принимают равные значения в точках, абсциссы которых равны по абсолютной величине, но противоположны по знаку. Иначе говоря, ординаты графика функции y = f(-x) в области положительных (отрицательных) значений х будут равны ординатам графика функции y = f(x) при соответствующих по абсолютной величине отрицательных (положительных) значениях х. Таким образом, получаем следующее правило. Для построения графика функции y = f(-x) следует построить график функции y = f(x) и отразить его относительно оси ординат. Полученный график является графиком функции y = f(-x) 4.2.2 Построение графика функции вида y = - f(x)f(x) => - f(x) Ординаты графика функции y = - f(x) при всех значениях аргумента равны по абсолютной величине, но противоположны по знаку ординатам графика функции y = f(x) при тех же значениях аргумента. Таким образом, получаем следующее правило. Для построения графика функции y = - f(x) следует построить график функции y = f(x) и отразить его относительно оси абсцисс. 4.2.3 Построение графиков четной и нечетной функцийКак уже отмечалось, для четной функции y = f(x) во всей области изменения ее аргумента справедливо соотношение f(x) = f(-x). Следовательно, функция такого рода принимает одинаковое значение при всех значениях аргумента, равных по абсолютной величин, но противоположных по знаку. График четной функции симметричен относительно оси ординат. Для построения графика четной функции y = f(x) следует построить ветвь графика этой функции только в области положительных значений аргумента (х³0). График функции y = f(x) в области отрицательных значений аргумента симметричен построенной ветви относительно оси ординат и получается отражением ее относительно этой оси. Для нечетной функции y = f(x) в области всех значений аргумента справедливо равенство f(-x) = - f(x). Таким образом, в области отрицательных значений аргумента ординаты графика нечетной функции равны по величин, но противоположны по знаку ординатам графика той же функции при соответствующих положительных значениях х. График нечетной функции симметричен относительно начала координат. Для построения графика нечетной функции y = f(x) следует построить ветвь графика этой функции только в области положительных значений аргумента (х³0). График функции y = f(x) в области отрицательных значений аргумента симметричен построенной ветви относительно начала координат и может быть получен отражением этой ветви относительно оси ординат с последующим отражением в области отрицательных значений относительно оси абсцисс. 4.2.4 Построение графика обратной функцииКак уже отмечалось, прямая и обратная функции выражают одну и ту же зависимость между переменными х и у, с тем только отличием, что в обратной функции переменные поменялись ролями, что равносильно изменению обозначений осей координат. Поэтому графиком обратной функции симметричен графику прямой функции относительно биссектрисы I и III координатных углов, т.е. относительно прямой y = x. Таким образом, получаем следующее правило. Для построения графика функции y = j(x), обратной по отношению к функции y = f(x), следует построить график y = f(x) и отразить его относительно прямой y = x. 4.3 Деформация4.3.1 Деформация графика вдоль оси ординатf(x) => A·f(x) Рассмотрим функцию вида y = A·f(x), где A>0. Нетрудно заметить, что при равных значениях аргумента ординаты графика этой функции будут в A раз больше ординат графика функции у = f(x) при A>1 или 1/A раз меньше ординат графика функции y = f(x) при A<1. Таким образом, получаем следующее правило. Для построения графика функции y = A·f(x) следует построить график функции y = f(x) и увеличить его ординаты в A раз при A>1(произвести растяжение графика вдоль оси ординат) или уменьшить его ординаты в 1/A раз при A<1(произвести сжатие графика вдоль оси ординат). Полученный график является графиком функции y = A·f(x). 4.3.2 Деформация графика вдоль оси абсциссf(x) => f(ωx). Пусть требуется построить график функции y = f(ωx), где ω>0. Рассмотрим функцию y = f(x), которая в произвольной точке x = x1 принимает значение y1 = f(x1). Очевидно, что функция y = f(ωx) принимает такое же значение в точке x = x2, координата которой определяется равенством x1 = ωx2, причем это равенство справедливо для совокупности всех значений х из области определения функции. Следовательно, график функции y = f(ωx) оказывается сжатым (при ω<1) или растянутым (при ω>1) вдоль оси абсцисс относительно графика функции y = f(x). Таким образом, получаем правило. Для построения графика функции y = f(ωx) следует построить график функции y = f(x) и уменьшить его абсциссы в ω раз при ω>1 (произвести сжатие графика вдоль оси абсцисс) или увеличить его абсциссы в 1/ω раз при ω<1 (произвести растяжение графика вдоль оси абсцисс). Полученный график является графиком функции y = f(ωx). 4.4 Алгебраические операции над графиками функцийРассмотрим основные алгебраические действия над функциями и их графиками, такие как сложение и вычитание (y = f(x) ±g(x)), умножение (y = f(x) ·g(x)), деление (y = f(x) / g(x)). При построении такого типа графиков следует учитывать, что область определения функции y является общей частью областей определения каждой из функций f(x) и g(x). Использование изложенных ниже методов построения графиков особенно целесообразно в случае, когда f(x) и g(x) являются элементарными функциями разных типов. 4.4.1 График суммы (разности) функцийy = f(x) ±g(x) График следует строить по точкам, складывая или вычитая ординаты графиков функций f(x) и g(x), соответствующие одному и тому же значению аргумента (разумеется, сначала строятся графики функций f(x) и g(x)). При построении графика разности функций обычно не прибегают к вычитанию графиков, а строят сначала график функции - g(x) и затем складывают графики f(x) и - g(x). 4.4.2 График произведения функцийy = f(x) ·g(x). Для построения графика данной функции надо построить графики функций f(x) и g(x) и перемножить значения ординат, соответствующие одним и тем же значениям аргумента. 4.4.3 График функции вида
Для построения такого графика следует построить график функции y1 = f(x) и, деля, единицу на численные значения ординат этой функции с учетом знака, по точкам построить график данной функции. При этом областью определения функции у является область определения функции y1 = f(x), за исключением тех значений х, при которых f(x) =0. В этих точках функция y =1/f(x) не определена (как правило, здесь имеются вертикальные асимптоты). При f(x) → ± ∞ у→0, при f(x) = ±1 у=±1 (т.е. значения заданной функции у и функции y1 = f(x) совпадают) 4.4.4 График частного двух функцийy = f(x) / g(x). Данную функцию можно представить в виде
Построение графика функции сводится к построению графиков функций y1 = f(x) и y2 = 1/g(x) и последующему перемножению по точкам значений соответствующих ординат этих графиков с учетом знака. 4.5 Построение графиков сложных функцийПрежде, чем приступить к построению графика сложной функции j [f(x)], необходимо сначала построить график функции f(x), а затем по точкам строить график сложной функции, проводя операцию взятия функции от функции. Рассмотрим ряд важнейших частных случаев. 4.5.1 График функции у = [f(x)] kДля построения графика функции у = [f(x)] k следует построить график y1 = f(x) и, возведя значения ординат построенного графика в степень k, по точкам построить график заданной функции. Отметим, что в общем случае число k может быть как
целым, так и дробным. Если возведение в степень k сводится к операции
извлечения корня четной степени (например, 4.5.2 График функции у = af(x)Для построения графика функции у = af(x) следует построить график y1 = f(x), а затем, возведя основание в степень, равную значению ординат графика, по точкам построить график заданной функции. При этом в точках, где f(x) =0, у=1, в точках, где f(x)
=1, у=а. Для случая а>1 при f(x) → ∞ y → ∞, а при f(x) →
- ∞ y →
0; для случая а<1 при f(x) → ∞ y → 0, а при f(x) →
- ∞ y →
∞. На практике при построении графиков случай а<1 удобно сводить к случаю
а>1 (например, В этой главе были рассмотрены наиболее известные и повсеместно используемые в математике методы построения графиков сложных функций. Так же эта глава насыщенна наиболее интересными и полезными потенциальными знаниями для ученика. Глава V: Графики нетрадиционных функций1. График функции Нам дана функция:
Найдем область допустимых значений для этой функции:
В знаменателе мы видим формулу разности квадратов, раскроем ее и представим в виде:
После сокращения мы получили следующий результат:
Раскроем модуль и получим:
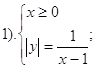
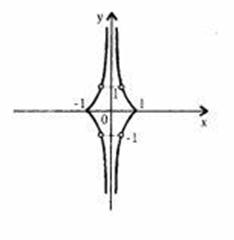
2. График функции Нам дана функция:
Найдем область допустимых значений для этой функции:
В числителе видим формулу разности квадратов, раскроем ее и представим в виде:
После сокращения мы получили следующий результат:
Соберем слагаемые, содержащие переменную “у” слева, а слагаемые, содержащие переменную “x” и свободные члены справа, получим:
Раскроем модуль и получим:
3. График функции График задан функцией:
Построим график, раскрывая модуль.
Приведя подобные, получим:
После приведения подобных и применения соответствующих действий над ними, мы получим ниже приведенное:
4. График функции График задан функцией:
Найдем область допустимых значений для этой функции.
В знаменателе функции заметна формула разности квадратов, раскроем ее следующим образом:
После нетрудных сокращений получаем:
Раскроем модуль, содержащийся в знаменателе дроби функции, ниже приведенным образом:
ЗаключениеВ первой главе была рассмотрена история возникновения функций и их графиков. На протяжении всей этой главы можно проследить историю развития понятия функции и применение ее в различных областях жизнедеятельности человека со времен глубокой древности до наших дней. Во второй главе были изложены основные понятия и положения о функциях и их графиках. Так же эта глава содержит такой параграф, как способы задания функций. Тема этого параграфа - неотъемлемая часть понятия функции. Основным достижением этой главы можно считать систематизация старых знаний с добавлением части новых. Третья глава содержит в себе три параграфа: простейшие функции, тригонометрические функции и кривые второго порядка. В параграф простейшие функции изложены основные положения и исследования о таких функциях, как линейная, прямая пропорциональность, обратная пропорциональность, гипербола, квадратичная, степенная и многие другие функции. В параграфе тригонометрические функции систематизированы знания обо всех прямых тригонометрических функциях. Они приведены в таблице. В параграфе кривые второго порядка рассмотрены такие графики как окружность и эллипс. Эта глава являет в себе большую научную ценность. Четвертая же глава содержит огромный полезный материал для практического применения. В ней были рассмотрены разнообразнейшие методы и способы построения сложных графиков функций. Эти приемы построения могут пригодиться на уроках алгебры для более быстрого и рационального построения графиков функций. В пятой главе изложены "решения" графиков нетрадиционных функций. Так же эта глава имеет практическую ценность. В этом реферате достигнуты все цели и выполнены основные задачи. Реферат необходим для классификации старых и изучения новых знаний и положений. Список литературы1. Виленкин Н.Я., "Функции в природе и технике", М., 1978; 2. Сивашинский И.Х., "Элементарные функции графики", М., 1965; 3. Дронов А.М., "Графики функций", М., 1972; 4. Валуцэ И.И., "Математика для техникумов", М., 1989; 5. Столин А.В., "Комплексные упражнения по математике", Харьков, 1995; 6. Кушнир И., "Шедевры школьной математики", Киев, 1995; 7. Мордкович А.Г., "Алгебра 9 класс", М., 2002; 8. Мордкович А.Г., "Алгебра и начала анализа 10-11 классы", М., 2004. Приложение 1
Приложение 2
Приложение 3
Приложение 4
Приложение 5
Приложение 6
Приложение 7
Приложение 8
Приложение 9
Приложение 10
Приложение 11
Приложение 12
Приложение 13
Приложение 14.
Приложение 15
|