|
Рефератыкосмонавтике административному праву хозяйственному праву устройствам экологическому праву криминалогия гражданский и землепользование обществознание |
Курсовая работа: Вариации при исчисленииКурсовая работа: Вариации при исчислении1. Элементы вариационного исчисления 1.1 Понятие функционала и оператораВ курсе высшей математики вводилось понятие функции. Если некоторому числу x из области D ставится в соответствие по определенному правилу или закону число y, то говорят, что задана функция y = f(x). Область D называют областью определения функции f(x). Если же функции y(x) ставится в соответствие по определенному правилу или закону число J, то говорят, что задан функционал J = J(y). Примером функционала может быть определенный интеграл от функции y(x) или от некоторого выражения, зависящего от y(x),
Если теперь функции y(x) ставится в соответствие по определенному правилу или закону вновь функция z(x), то говорят, что задан оператор z = L(y), или z = Ly. Примерами дифференциальных операторов могут служить:
Дадим более строгое определение функционала. Пусть A – множество элементов произвольной природы, и пусть каждому элементу u є A приведено в соответствие одно и только одно число J(u). В этом случае говорят, что на множестве A задан функционал J. Множество A называется областью определения функционала J и обозначается через D(J); число J(u) называется значением функционала J на элементе u. Функционал J называется вещественным, если все его значения вещественны. Функционал J называется линейным, если его область определения есть линейное множество и если J (αu + βv) = αJ(u) + βJ(v). 1.2 Задачи, приводящие к экстремуму функционала
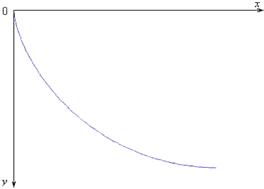
Задача о брахистохронеЗарождение вариационного исчисления относят обычно к 1696 г., когда И. Бернулли поставил так называемую задачу о брахистохроне: точки А (0,0) и В (а, b) расположены в вертикальной плоскости (xy) (рис. 1). Какова должна быть кривая, лежащая в плоскости (xy) и соединяющая точки А и В, чтобы материальная точка, двигаясь без трения, скатывалась по этой кривой из точки А в точку В в кратчайшее время? Искомая кривая и была названа брахистохроной. Пусть
уравнение кривой АВ есть y = u(x).
Рассмотрим некоторый момент времени t, и пусть
в этот момент движущаяся точка находится на расстоянии y от оси x. Тогда
Отсюда
Обозначим через Т время, в течение которого материальная точка достигает точки В. Интегрируя, находим
Задача сводится к следующему: надо найти функцию y = u(x), удовлетворяющую условию u(0) = 0; u(а) = b (1.2) и сообщающую интегралу (1.1) наименьшее значение. Условия (1.2) означают, что искомая кривая должна проходить через заданные точки А и В. Такого типа условия принято называть граничными, или краевыми, так как они относятся к концам промежутка, на котором должна быть определена искомая функция. Примером применения кривой в виде брахистохроны служит образующая цилиндрических поверхностей, используемых на детских площадках, в аттракционах для спуска с возвышения, на трамплинах. Задача о наибольшей площадиСформулируем
эту задачу так: среди всех плоских кривых, имеющих данную длину Пусть уравнение кривой будет y = u(x). Задача заключается в том, чтобы найти функцию u(x), удовлетворяющую краевым условиям u(а) = u(b) = 0 (1.3) и тождеству
и сообщающую интегралу
наибольшее значение. Общим для рассмотренных задач является то, что каждый раз ищется функция, удовлетворяющая тем или иным поставленным условиям и сообщающая экстремальное значение заданному функционалу. Приведенные здесь задачи относятся к ветви математического анализа, называемой вариационным исчислением. 1.3 Постановка задачи вариационного исчисленияЗадача вариационного исчисления состоит в следующем: дан функционал J с областью определения D(J); требуется найти элемент u0 є D(J), сообщающий функционалу либо минимальное значение
либо максимальное значение
Задача о максимуме функционала J тождественна с задачей о минимуме функционала – J, поэтому в дальнейшем будем рассматривать только задачу о минимуме функционала J. В приведенной общей формулировке задачу вариационного исчисления решить вряд ли возможно, поэтому наложим на функционал J некоторые ограничения. Будем считать, что D(J) есть часть некоторого пространства Х. Чтобы сформулировать дальнейшие ограничения, введем понятие линейного многообразия. Пусть М – линейное множество элементов пространства Х и ū – некоторый фиксированный элемент этого пространства. Линейным многообразием в пространстве Х назовем совокупность элементов, каждый из которых можно представить в виде u = ū + η, ηєМ. (1.8) Если ūєМ, то, очевидно, так определенное линейное многообразие совпадает с М. Требование 1. Область определения D(J) функционала J есть линейное многообразие. Будем считать также, что пространство Х бесконечномерно. Тогда в Х линейное множество М также бесконечномерно и, следовательно, из него можно выделить конечномерное подпространство. Требование 2. Если η пробегает любое конечномерное подпространство, содержащееся в М, то на этом подпространстве функционал J(u) = J (ū + η) непрерывно дифференцируем достаточное число раз. Введем понятие об абсолютном и относительном минимуме функционала. Функционал J достигает на элементе u0 є D(J) абсолютного минимума, если неравенство J(u0) = J(u) (1.9) Справедливо для любого элемента u є D(J). Тот же функционал достигает на элементе u0 относительного минимума, если неравенство (9) справедливо для элементов u є D(J), достаточно близких к u0. Абсолютный минимум называют еще сильным минимумом, а относительный – слабым. Существует аналогия между нахождением минимума функции и минимума функционала. При нахождении минимума функции первая производная функции приравнивается к нулю и находится точка, подозрительная на экстремум. Затем с помощью второй производной проверяется достаточное условие экстремума. При нахождении минимума функционала находится первая вариация функционала и приравнивается к нулю. В результате получаем необходимое условие экстремума функционала. Для проверки достаточного условия экстремума функционала находится вторая вариация функционала. 1.4 Первая вариация и градиент функционалаБудем рассматривать функционал J, подчиненный требованиям 1, 2. Возьмем произвольный элемент u є D(J) и произвольный элемент η є М. Обозначим через α произвольное вещественное число. Нетрудно видеть, что элемент u + αη є D(J). (1.10) Составим выражение J (u + αη). В силу требования 2 J (u + αη) есть непрерывно дифференцируемая функция от α. Вычислим ее производную и возьмем значение этой производной при α = 0
В результате получим число, которое можно рассматривать как значение функционала (11), зависящего от двух элементов u и η. Определение. Функционал
называется первой вариацией функционала J на элементе u и обозначается символом δJ (u, η):
При этом разность двух функций u є D(J) и u1 є D(J) называют вариацией функции u и обозначают δu = u(х) – u1 (х). Пример. Найти первую вариацию функционала
область определения которого D(J) состоит из
функций, удовлетворяющих следующим условиям: u u(а) = А, u(b) = В, (1.14) где А и В-заданные постоянные. Условия (14)
означают, что кривые у = u(х), где u Несложно показать, что функционал (13) удовлетворяет оговоренным выше двум требованиям, кроме того, он удовлетворяет требованию 3. Требование 3. Вариация δJ (u, η) – не только однородный, но и аддитивный функционал от η. Составим вариацию функционала (1.13)
Можно показать, что интеграл:
есть ограниченный функционал от η, при этом считаем, что η(х) непрерывно дифференцируема и удовлетворяет условиям: η(а) = η(b) = 0. (1.17) В этом случае интеграл (1.16) можно взять по частям
Таким образом, интеграл (1.15) можно записать в виде
Здесь u + αη – u = αη = δu u можно записать
Вариацию δJ (u, η) можно записать в виде δJ (u, η) = (Рu, η). (1.20) Определение. Оператор Р, определенный формулой (1.20), называется градиентом функционала J(u) и обозначается символом Р = grad J. Если u δJ (u, η) = (grad J(u), η) (1.21) Здесь взяли α = 1, чтобы не загромождать запись. В выражении (1.18)
1.5 Необходимое условие минимума функционалаПусть функционал J достигает на некотором
элементе u0 относительного минимума. Возьмем произвольный элемент η J(u0 + αη) Это неравенство означает, что функция одной вещественной переменной α, равная J(u0 + αη), имеет при α0 = 0 относительный минимум. Но тогда необходимо
или, что то же δJ(u0, η) = 0 (1.23) Если функционал в некоторой точке достигает минимума, то в этой точке первая вариация функционала равна нулю. В этом заключается необходимое условие экстремума функционала. 1.6 Уравнение Эйлера. Связь между вариационной и краевой задачамиРассмотрим основную лемму вариационного исчисления. Лемма Лагранжа. Пусть f (х, у) – функция, непрерывная в области D с контуром Г. Если
для любой функции η (х, у), непрерывной в области D вместе со своими частнымы производными до n-го порядка включительно и обращающейся в нуль на границе Г (η (х, у)|Г = 0), то f (х, у) = 0. Для примера, рассмотренного в 1.4, было получено в точке минимума функционала (1.13) условие
Исходя из леммы Лагранжа, можем записать
Если условие (1.25) записать в виде
то очевидно, что δu (вариация искомой функции) – функция неравная нулю на отрезке (а, b), поэтому должно выполняться условие (1.26). Уравнение (1.26) можно еще записать в виде
Уравнение (1.26) называют уравнением Эйлера. Если предположить существование непрерывной второй производной от u(х), то уравнение (1.26) можно записать в виде
Таким образом, условие минимума функционала (1.13) при условии (1.14) приводит к краевой задаче для уравнения Эйлера (1.26) при тех же условиях (1.14), т.е. Существует тесная связь между вариационной задачей о минимуме функционала и краевой задачей для уравнения Эйлера для этого функционала. Решения уравнения Эйлера (1.26), удовлетворяющие условиям (1.14) называют экстремалями функционала (1.13). 1.7 Пути решения вариационных задачОдин из путей решения вариационной задачи, т.е. задачи нахождения минимума некоторого функционала J(u) при заданных краевых условиях, состоит в сведении этой задачи к краевой задаче для дифференциального уравнения при тех же краевых условиях, которое является уравнением Эйлера для этого функционала, с последующим решением этой задачи. Второй путь решения вариационной задачи состоит в применении вариационных методов, которые позволяют приближенно найти функцию u0, дающую минимум функционалу J(u), и удовлетворяющую заданным краевым условиям. Рассмотрим несколько примеров решения задач вариационного исчисления, основанных на нахождении уравнений Эйлера с последующим их решением. Пример 1. Найти функцию у = u(х), удовлетворяющую условию u(0) = u(1) = 0 (1.27) и дающую минимум функционалу
Будем считать, что функция u(х) непрерывна и имеет непрерывные производные до второго порядка включительно. Уравнение Эйлера для функционала (28) будет иметь вид
Таким образом, получили краевую задачу для линейного дифференциального уравнения второго порядка с постоянными коэффициентами. Общее решение уравнения (1.29) будет иметь вид
Для нахождения произвольных постоянных с1 и с2 воспользуемся краевыми условиями (1.27). В результате получим
Откуда
Следовательно, функция, дающая минимум функционалу (1.28) при условии (1.27), будет иметь вид
Пример 2. В качестве второго примера рассмотрим задачу о брахистохроне. Как было показано ранее (см. 1.2.1), задача состоит в том, чтобы найти функцию у = u(х), удовлетворяющую условиям: u(0) = 0, u(а) = b и сообщающую минимум функционалу
В этом случае
Функция (31) при u = 0 терпит разрыв. Путем несложных рассуждений показывается, что все-таки можно воспользоваться уравнением Эйлера в виде (1.26). Уравнение (1.26) приводится к виду
Отсюда
Положим
Дифференцируя
это выражение, получим
Далее
Положив
Таким образом, если решение задачи о брахистохроне имеет решение, то это решение есть циклоида. 1.8 Вторая вариация функционала. Достаточное условие минимума функционалаРассмотрим
функцию Эту функцию разложим в ряд Тейлора:
где R1 – остаточный член ряда. Выражение
называется второй вариацией функционала J на элементе u. Разложение (1.34) можно записать в виде
Пусть
функционал J достигает минимума,
относительного или абсолютного на элементе u0. Тогда
Из
этого соотношения вытекает достаточное условие того, что элемент u0,
удовлетворяющий уравнению Эйлера (экстремаль), сообщает функционалу минимальное
значение. Для абсолютного минимума это условие имеет вид (учитывая, что
для
относительного минимума оно состоит в том, что неравенство (1.38) выполняется,
когда элемент Условие
(1.38) в конкретных задачах трудно проверить, потому что величина Поэтому для проверки достаточного условия экстремума функционала пользуются более простыми условиями. Запишем вторую вариацию для функционала (1.13)
пользуясь определением второй вариации (1.35)
где
Так
как
где
Считаем,
что необходимое условие экстремума выполнено, т.е. Условие
называют условием Лежандра. Более сильное условие
называют усиленным условием Лежандра. Рассмотрим
интеграл, входящий в формулу (1.39), заменяя букву
Уравнение Эйлера для этого интеграла будет иметь вид
причем,
с непрерывными в [a, b] коэффициентами p(x) и q(x). Уравнение (1.40) называют уравнением Якоби. Пусть
Существенным
для дальнейшего будет тот факт, имеет ли решение Если
Имеет место следующая теорема. Усиленные условия Лежандра и Якоби достаточны для того, чтобы экстремаль давала слабый (местный) экстремум функционалу (1.13). Можно
показать, что если выполнены усиленные условия Лежандра и Якоби и, кроме того, Пример. Докажем, что экстремаль (1.30) (см Пример 1 в 1.8) дает функционалу (1.28) сильный минимум. Из (1.28) имеем
Уравнение (1.40) принимает вид
его
решение при условии
Функция
1.9 Изопериметрическая задачаИзопериметрическая
задача ставится следующим образом: Даны функционалы
требуется найти элемент, доставляющий функционалу J наименьшее значение. Считается, что область
не пуста. Частным случаем изопериметрической задачи является задача о наибольшей площади, поставленная в 2.2. Здесь n=1.
За D(J) можно
принять множество тех функций из С [a, b], которые
обращаются в нуль при x=a и x=b (условие
3), а за Будем
считать, что множество Справедлива теорема, принадлежащая Эйлеру и известная под названием правила множителей для изопериметрической задачи. Теорема
Эйлера: Пусть элемент
отличен
от нуля, то найдутся такие постоянные
Рассмотренная теорема дает только необходимое условие минимума для изопериметрической задачи. Техника решения изопериметрической задачи такова: составляя функционал
где
В
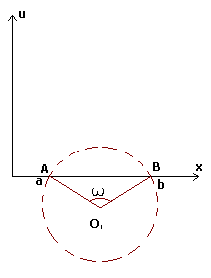
качестве примера рассмотрим задачу о наибольшей площади (см. 2.2). В
соответствии с теоремой Эйлера введем постоянный множитель
Уравнение Эйлера для функционала Э примет вид
Интегрирование дает
Отсюда
Интегрируя
еще раз, придем к уравнению окружности радиуса
Таким
образом, если решение существует, то это – дуга окружности. Для определения ее
радиуса
Пусть
Для
определения
решение
которого всегда возможно при указанном выше условии. Подставляя условия (1.3) в
уравнение (1.46) находим 1.10 Минимизирующая последовательностьПусть J-произвольный ограниченный снизу функционал. В этом случае существует нижняя грань его значений
Последовательность
Теорема 1: Функционал, ограниченный снизу, имеет по крайней мере одну минимизирующую последовательность. Из
определения нижней грани следует, что: 1) для любого элемента Теорема
2: Пусть D(J) – линейное
многообразие некоторого банахова пространства X. Если
функционал J непрерывен в D(J) и
существует предел минимизирующей последовательности Доказательство вытекает из непрерывности функционала
Теоремы 1, 2 создают возможность решать задачу о минимуме функционала, минуя уравнение Эйлера. Для этого надо прежде всего погрузить множество D(J) в такое банахово пространство X, в котором функционал J был бы непрерывен. Далее следует построить минимизирующую последовательность. Если она сходится, то ее предел решает вариационную задачу. На этом построены численные вариационные методы (см 15) и обоснование их сходимости. 1.11 Функционал от функций, нескольких независимых переменныхРассмотрим
конечную область Рассмотрим функционал
при
условии Найдем первую вариацию функционала (1.47)
Здесь обозначено
Пусть
функция
Тогда имеем
и, следовательно
В этом случае уравнение Эйлера для функционала (1.47) принимает вид
и называется уравнением Остроградского. Пример. Найти уравнение Эйлера для функционала
при
краевом условии Пусть
функция
1.12 Функционал от функций, имеющих производные высших порядковРассмотрим функционал вида
Будем
считать, что функция
и в этой области k раз непрерывно дифференцируема. Функционал
(1.52) зададим на функциях
где
Ai, Bi
– заданные постоянные. Возьмем функцию
Пусть
функция такова, что
и, следовательно,
Откуда получим уравнение Эйлера
с краевыми условиями (1.53). Сказанное выше переносится на случай функции многих независимых переменных. Для функционала
при краевых условиях
где Уравнение Остроградского будет иметь вид
Это уравнение должно решаться при краевых условиях (1.58) Пример. Выражение
полной энергии деформации жесткой пластинки (плиты) при малых перемещениях,
находящейся под действием поперечной нагрузки
где
W (x, y) – прогиб
пластинки;
Функция W (x, y) является непрерывной функцией, имеющую непрерывную производную до четвертого порядка включительно и все требования 1,2,3 будут выполнены. При шарнирно-неподвижном закреплении краев пластинки должны выполняться условия При x=0, x=a
При y=0, y=b
Получим уравнение Эйлера(Остроградского) для функционала (1.60) при краевых условиях (1.61), (1.62). Так как
то уравнение Остроградского принимает вид
При этом
Поставив эти выражения в (1.63), получим уравнение Остроградского для функционала (1.60)
Уравнение (1.64) является уравнением равновесия рассматриваемой пластины и должно решаться при граничных условиях (1.61), (1.62). 1.13 Функционалы, зависящие от нескольких функцийРассмотрим функционал
Зададим
его на парах
где
Множество
векторов Строим две функции, близкие к u(x) и v(x):
Подставив
их в функционал (1.65), получим функцию
Первая вариация функционала (1.65) выражается формулой
где
Откуда получаем уравнения Эйлера для функционала (1.65) в виде системы двух дифференциальных уравнений
Эти уравнения должны решаться при краевых условиях (1.66). 2. Вариационные задачи с подвижными границами 2.1 Простейшая задача с подвижными границамиВ гл. 1 при исследовании функционала
предополагается, что
граничные точки Предположим теперь, что
одна или обе граничные точки могут перемещаться, тогда класс допустимых кривых
расширяется. Поэтому, если на какой-нибудь кривой
Итак, кривые Общее решение уравнения Эйлера содержит две произвольные постоянные, для определения которых необходимо иметь два условия. В задаче с неподвижными граничными точками такими условиями были
В задаче с подвижными
границами одно или оба эти условия отсутствуют и недостающие условия для
определения произвольных постоянных общего решения уравнения Эйлера должны быть
получены из основного необходимого условия экстремума Допустимые кривые Экстремали, проходящие
через точку 2.2 Условие трансверсальности
Вычислим вариацию
функционала
Первое слагаемое правой части преобразует с помощью теоремы о среднем значении:
В силу непрерывности
функции
где Итак,
Второе слагаемое (3.1) преобразуем путем разложения подинтегральной функции по формуле Тейлора
где
может быть преобразована путем интегрирования по частям второго слагаемого подинтегральной функции к виду
Значение функционала берется лишь на экстремалях, следовательно
Итак, окончательно имеем:
где приближенные
равенства также справедливы с точностью до членов порядка выше первого
относительно Таким образом
Основное необходимое
условие экстремума
Если вариации
Однако чаще всего
вариации
Тогда
или, так как
Это условие устанавливает
зависимость между угловыми коэффициентами Условие трансверсальности
совместно с условием Пример. Найти условие трансверсальности для функционалов вида
Условие трансверсальности (3.3) имеет в данном случае вид
или
Полагая, что
или
Условие трансверсальности в данном случае свелось к условию ортогональности. 2.3 Задача с подвижными границами для функционалов от нескольких функцийЕсли при исследовании на экстремум функционала
одна из граничных точек,
например
Общее решение системы
уравнений Эйлера содержит четыре произвольные постоянные. Зная координаты
граничной точки Вычисление вариации
Применяя теорему о
среднем значении к первому интегралу и учитывая непрерывность функции
Откуда, учитывая
зависимость
Если граничная точка
переходит в условие
(считая
Это условие носит название условия трансверсальности в задаче об исследовании на экстремум функционала (3.4). Условие (3.7) совместно с
уравнениями Если граничная точка
Если рассматривать функционал
то в случае одной
подвижной точки
Пример. Найти условие трансверсальности для функционала
если Условия трансверсальности (3.8) в данном случае имеют вид
1. Найти экстремаль
функционала Пример 1.
Решение: Вычислим первую вариацию
функционала
После преобразования этого функционала получим
Произвольные функции В точке
Это уравнение приводится к виду
и должно решаться при
условии Имеем
откуда Таким образом, получаем
решение Исследовать функционал Пример 2.
Решение. Найдем первую
вариацию функционала
Необходимое условие
экстремума функционала в точке
Это уравнение при краевых
условиях
Так как в данном примере
и усиленное условие Лежандра
Уравнение Эйлера для
интеграла (1.39) (см. 1.8.) будет иметь вид (после замены
или
Откуда
Для нахождения Откуда
Проверим условие Якоби.
Решение
сильный (абсолютный) минимум. Список используемой литературы 1. Гельфанд И.М., Фомин С.В. Вариационное исчисление. М.: Наука. 1961. 2. Коршунов Ю.М., «Математические основы кибернетики», Москва, 1987 г.; 3. Таха Х., «Введение в исследование операций», Москва, 1985 г.; 4. Д. Сю., А. Мейер, «Современная теория автоматического управления и её применение», Машиностроение, 1972 г.; |
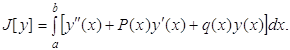
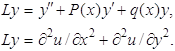
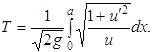 (1.1)
(1.1)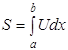 (1.5)
(1.5)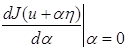 . (1.11)
. (1.11)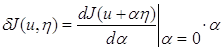 . (1.12)
. (1.12)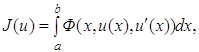 (1.13)
(1.13)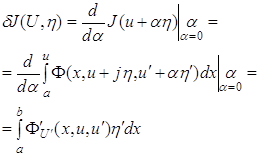 (1.15)
(1.15)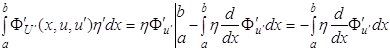
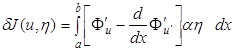 . (1.18)
. (1.18)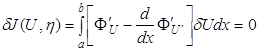 ,
,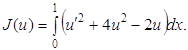 (1.28)
(1.28)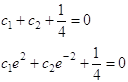
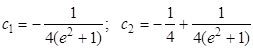
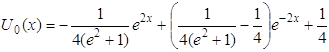 . (1.30)
. (1.30)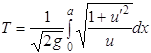 .
.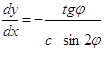
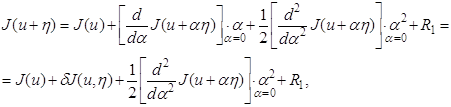 (1.34)
(1.34)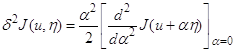
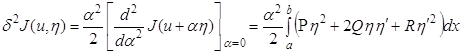 ,
,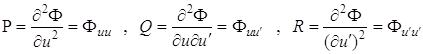 .
.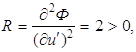 то и усиленное условие
Лежандра выполняется. Следовательно, экстремаль (1.30) даёт функционалу (1.28)
сильный (абсолютный) минимум.
то и усиленное условие
Лежандра выполняется. Следовательно, экстремаль (1.30) даёт функционалу (1.28)
сильный (абсолютный) минимум.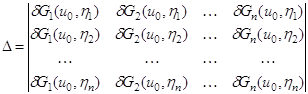 (1.43)
(1.43)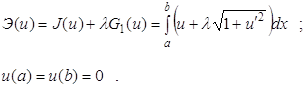
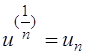 . Тогда
. Тогда 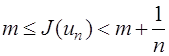 , откуда следует, что
, откуда следует, что 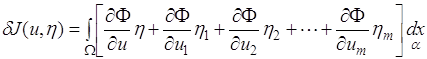 (1.48)
(1.48)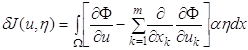 (1.49)
(1.49)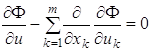 ,
, 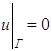 .
.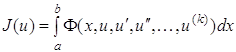 . (1.52)
. (1.52)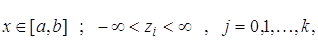
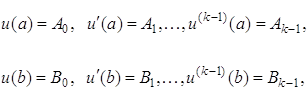 (1.53)
(1.53)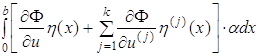 (1.54)
(1.54)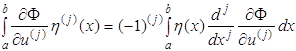
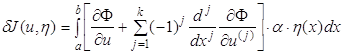 (1.55)
(1.55)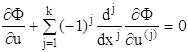 (1.56)
(1.56)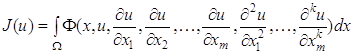 (1.57)
(1.57)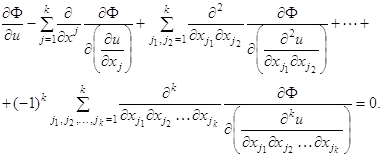 (1.59)
(1.59)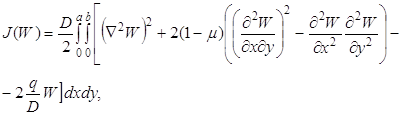 (1.60)
(1.60)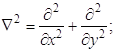 E,
E, 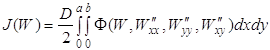
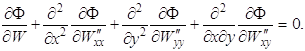 (1.63)
(1.63)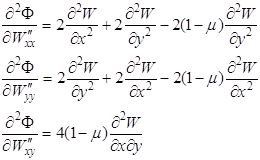
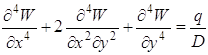 . (1.64)
. (1.64)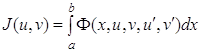 (1.65)
(1.65)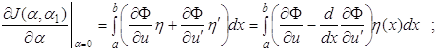
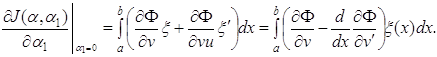
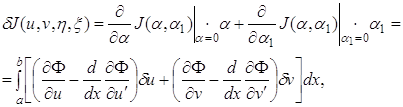
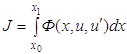
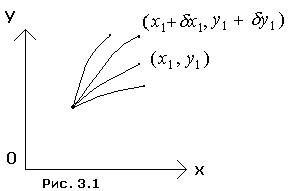
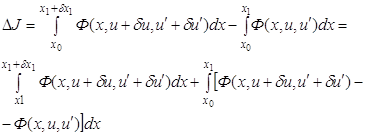 (3.1)
(3.1)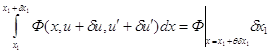 , где
, где 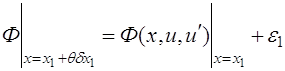 ,
,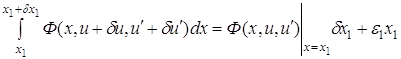 .
.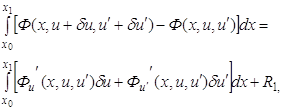
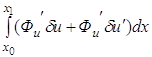
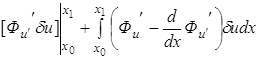 .
.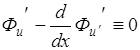 . Так как граничная точка
. Так как граничная точка 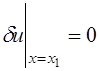 . Следовательно,
. Следовательно,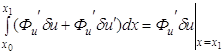 .
.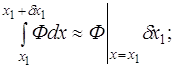
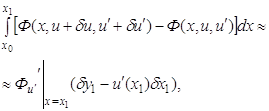
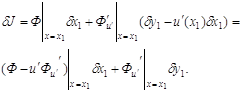
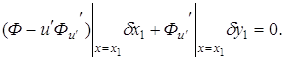 (3.2)
(3.2)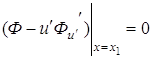 и
и 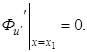
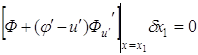
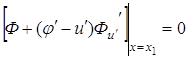 . (3.3)
. (3.3)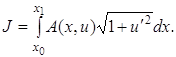
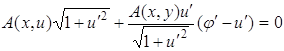
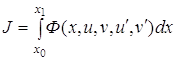 (3.4)
(3.4)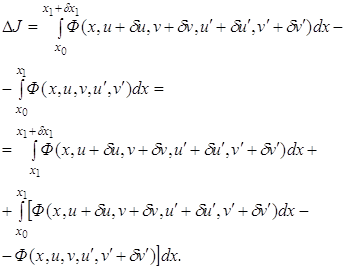
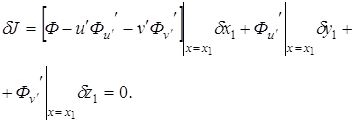 (3.6)
(3.6)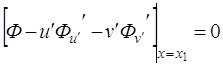 ,
, 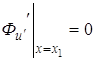 и
и 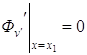 .
.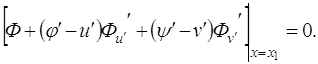 (3.7)
(3.7)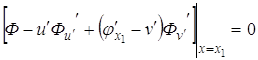 ,
,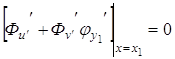 (3.8)
(3.8)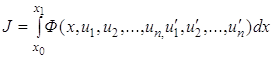 ,
,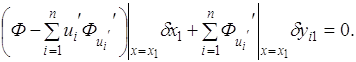
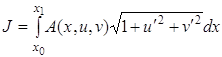 ,
,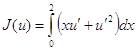 ,
,