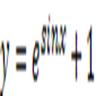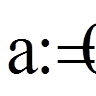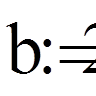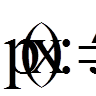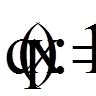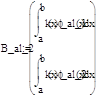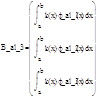|
Рефератыкосмонавтике административному праву хозяйственному праву устройствам экологическому праву криминалогия гражданский и землепользование обществознание |
Курсовая работа: Метод Галеркіна пошуку розв’язку лінійної крайової задачіКурсовая работа: Метод Галеркіна пошуку розв’язку лінійної крайової задачіУКООПСПІЛКА Полтавський університет споживчої кооперації України Кафедра математичного моделювання та соціальної інформатики
КУРСОВИЙ ПРОЕКТ з дисципліни ”Чисельні методи” на тему: Метод Галеркіна пошуку розв’язку лінійної крайової задачі Захищена на Виконав студент групи СІ-31 „_______________” спеціальності „Соціальна інформатика” „____” _____________200_ р. Буцький Владислав Володимирович Полтава – 2007 ЗМІСТ ВСТУП РОЗДІЛ 1. Теоретична частина 1.1. Постановка задачі 1.2. Математична модель РОЗДІЛ 2. Практична частина 2.1. Алгоритм методу 2.2. Блок-схема алгоритму 2.3. Тестовий приклад ВИСНОВОК СПИСОК ЛІТЕРАТУРНИХ ДЖЕРЕЛ Додаток А Вступ
В зв’язку з потребами нової техніки інженерна практика наших днів все частіше і частіше зустрічається з математичними задачами, точне розв’язання яких досить складне або невідоме. В цих випадках зазвичай вдаються до тих чи інших наближених обчислень. Ось чому наближені і чисельні методи математичного аналізу набули за останні роки широкого розвитку і отримали виключно важливе значення. Зростання продуктивних сил в ХХ сторіччі зумовило рішучий прогрес в області обчислювальної техніки, що привів до створення сучасних електронних обчислювальних машин з пограмним управлінням. Це необмежено розширило обчислювальні можливості математики: задачі, для вирішення яких при ручному обрахунку були потрібні роки, зараз розв'язуються за декілька годин, причому безпосередній обрахунок займає хвилини. У свою чергу, нові обчислювальні засоби викликали переоцінку відомих методів розв’язання задач з погляду доцільності їх реалізації на сучасних обчислювальних машинах і стимулювали створення більш ефективних прийомів. Сучасні електронні обчислювальні машини дали в руки дослідників ефективний засіб для математичного моделювання складних задач науки і техніки. Саме тому кількісні методи дослідження в даний час проникають практично у всі сфери людської діяльності, а математичні моделі стають засобом пізнання. Роль математичних моделей далеко не вичерпується проблемою пізнання закономірностей. Їх значення безперервно зростає у зв'язку з природною тенденцією до оптимізації технічних пристроїв і технологічних схем планування експерименту. В процесі пізнання і в прагненні створити детальну картину досліджуваних процесів ми приходимо до необхідності будувати все більш складні математичні моделі, які у свою чергу вимагають універсального тонкого математичного апарату. Реалізація математичних моделей на ЕОМ здійснюється за допомогою методів обчислювальної математики, яка безперервно удосконалюється разом з прогресом в області електронно-обчислювальної техніки. Всяка редукція задач математичної фізики або техніки зрештою звичайно зводиться до рівняння алгебри тієї або іншої структури. Тому предмет обчислювальної математики, як правило, пов'язаний з методами зведення задач до систем рівнянь алгебри і їх подальшого розв’язання. Чисельні методи сьогодні - один з найпотужніших математичних засобів розв’язування задач. Найпростіші чисельні методи ми використовуємо постійно, наприклад, добуваючи квадратний корінь на аркуші паперу. У той час є задачі, де без достатньо складних чисельних методів не можна було б отримати відповіді; класичний приклад – відкриття Нептуна по аномаліях руху Урана. Чисельні методи є основним інструментом розв’язання сучасних прикладних задач. Аналітичний розв’язок тієї або іншої задачі є швидше виключенням, ніж правилом через складний і наближений характер досліджуваних моделей. От чому чисельний аналіз математичних моделей - метод, алгоритм, програма, обчислювальний експеримент - є в сьогоденні актуальним і найбільш ефективним апаратом конструктивного дослідження прикладних проблем. РОЗДІЛ 1. Теоретична частина 1.1 Постановка задачі Крайова задача – це задача знаходження власного роз’язку системи:
на відрізку Свою первинну назву цей тип задач отримав з найпростіших випадків, коли
частина додаткових умов задається на одному кінці відрізка, а інша частина – на
другому (тобто тільки в точках х=а і х=b). Прикладом є
задача знаходження статистичного прогину
тут Для рівнянь або систем більш високих порядків, де число додаткових умов більше за два, постановки крайових умов більш різнобічні. При цьому можливі випадки, коли частина умов задана у внутрішніх точках відрізка [a, b]; їх нерідко називають внутрішніми крайовими умовами. Наприклад, статистичний прогин навантаженого пружного бруска задовольняє рівнянню четвертого порядку
якщо цей брусок лежить в точках
тобто всі вони задані в різних точках. Самі додаткові умови можуть зв’язувати між собою значення кількох функцій в одній точці (або навіть в різних точках); тоді для системи р-го порядку вони приймуть вигляд
Існують задачі з ще більш складнішими за формою крайовими умовами, наприклад, умовами нормування
звичними в квантовій механіці, і т. д. Не дивлячись на різноманітність форм крайових умов, крайові задачі розв'язуються в основному одними і тими ж чисельними методами, що виправдовує їх об'єднання в один тип. Зупинимося на методах розв’язування. Знайти точний роз’язок крайової задачі в елементарних функціях вдається рідко: для цього треба знайти загальний розв’язок системи (1) і зуміти явно визначити з крайових умов значення сталих, що входять у нього. До наближених методів розв’язку крайових задач відносяться розклад в ряди Фур’є, методи Рітца і Галеркіна. Ряди Фур’є застосовуються до лінійних задач. Інші два методи застосовуються і до деяких нелінійних задач. Для чисельного розв’язку крайових задач використовують метод стрільби і різницевий метод. Метод стрільби базується на зведенні крайової задачі до деякої задачі Коші для тієї ж системи рівнянь. В різницевому методі задача наближено заміняється розв’язком алгебраїчної системи рівнянь з досить великим числом невідомих. У випадку нелінійних задач обидва методи є ітераційними; при цьому побудова ітераційних процесів, що добре збігаються, виявляється достатньо складною. Математична модель задачі Методи приблизного розв’язання поставлених крайових задач можна розбити на дві групи: різницеві методи і аналітичні методи. До різницевих методів розв’язку лінійної крайової задачі відносять: метод скінченних різниць для лінійних диференціальних рівнянь другого порядку, метод прогонки. До аналітичних методів – метод Галеркіна, метод колокацій. Метод скінченних різниць дозволяє знайти наближений розв’язок крайової задачі у вигляді таблиці, а аналітичні методи дають можливість знайти наближений розв’язок лінійної крайової задачі у вигляді аналітичного виразу. Розглянемо метод Галеркіна для знаходження наближеного розв’язку лінійної крайової задачі. Метод Галеркіна базується на одній теоремі з теорії загальних рядів Фур’є. Теорема. Нехай то Доведення. Розглянемо ряд Фур’є функції Як відомо, коефіцієнти Фур’є
В силу умови (3) маємо Для повної системи Звідси, враховуючи рівність (5), маємо
і, отже, Зауваження. З формули (4) випливає, що якщо неперервна функція ортогональна до кінцевої системи функцій
при достатньо великому N. В цьому
випадку функція Перейдемо до викладу метода Галеркіна. Нехай маємо лінійну крайову задачу де
Оберемо кінцеву систему базисних функцій
а функції
Розв’язок крайової задачі (7) – (8) будемо, як звичайно, шукати у вигляді При нашому підборі базисних функцій
Для точного розв’язку у нашій крайовій задачі функція Згідно методу Галеркіна вимагаємо, щоб нев’язність Наскільки цей наближений розв’язок
близький до точного, в загальному випадку питання залишається відкритим. Таким чином, для
визначення коефіцієнтів
або, більш детально, ( РОЗДІЛ 2. ПРАКТИЧНА ЧАСТИНА 2.1. Алгоритм методу
1. Визначаємо з даного диференціального рівняння другого порядку функції 2. Обираємо систему базисних функцій 3. Знаходимо 4. Використовуючи позначення
обраховуємо коефіцієнти системи:
5. Виконуючи необхідні скорочення приходимо до системи з якої визначаємо
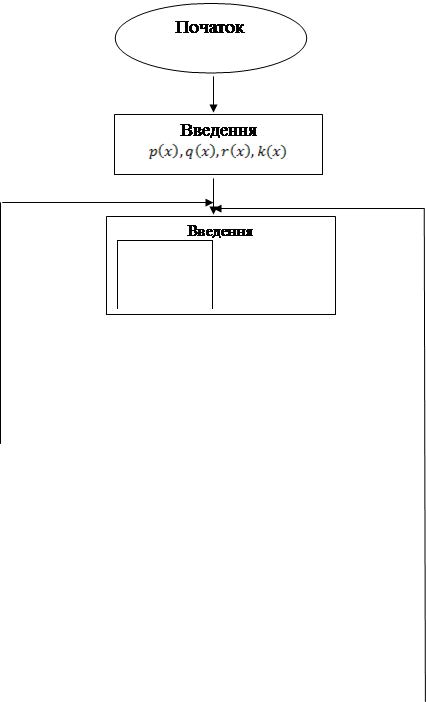
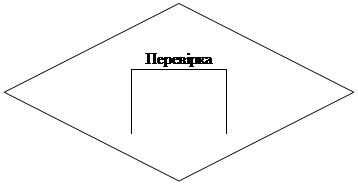
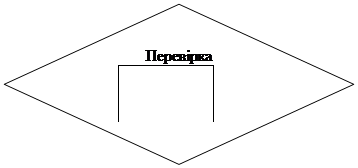
2.2. БЛОК-СХЕМА АЛГОРИТМУ Метод Галеркіна
Ні
Так
Ні
2.3. Тестовий приклад Методом Галеркіна знайти наближений розв’язок рівняння,
що задовольняє крайовим умовам
Розв’язання: Оберемо в якості системи базисних функцій
Ці функції лінійно незалежні на відрізку
Знаходимо Обраховуємо коефіцієнти системи (10), використовуючи наступні позначення:
і враховуючи при цьому ортогональність системи тригонометричних функцій (1, Виконуючи відповідні скорочення, приходимо до системи
з якої одержуємо
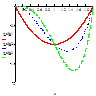
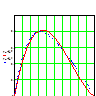
В таблиці 1
наведено для порівняння значення
отриманого наближеного розв’язку і точного розв’язку Наближений і точний розв’язок задачі (11), (12) Таблиця 1:
A_al_2:= [на дискеті, Галеркін.mcd]
A_al_3:= [на дискеті, Галеркін.mcd]
Результати отримані за допомогою створеної програми
ВИСНОВОК Математичне моделювання процесів і явищ в різних галузях науки і техніки є одним з головних способів отримання нових знань і технологічних рішень. В наш час коли життя людини вже майже неможливе без електронно-обчислювальної техніки, всі процеси автоматизуються, а задачі, які потребували деякого часу і зусиль тепер виконуються за лічені хвилини. Чисельні методи один із напрямів розробки пошуку оптимальних розв’язків математичних задач та пошуку саме того методу, який би давав найбільш точний результат. Моя робота присвячена одному з методів пошуку розв’язку лінійної крайової задачі – методу Галеркіна. Даний метод досить зручний для пошуку розв’язку у вигляді аналітичного виразу. В першій частині курсового проекту розглянута постановка задачі, в якій наведено опис методу. В математичній моделі описано безпосередньо сам метод Галеркіна та його основні принципи. Друга частина мого курсового проекту починається з опису алгоритму методу Галеркіна для пошуку розв’язку лінійної крайової задачі. В алгоритмі містяться головні кроки пошуку розв’язку лінійної крайової задачі за даним мені методом. За цим алгоритмом наведений тестовий приклад, а також написана програма в середовищі Microsoft Visual C++, текст якої знаходиться в додатку А. До даного методу складена блок-схема алгоритму. СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ 1. Капченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. – М: Наука, 1972. – 369 С. 2.Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Физматгиз, 1960. - 659с. 3.Калиткин Н.Н. Численные методы. - М.: Наука, 1978. - 512с. 4. Бахванов Н. С., Жидков Н.П. Кобельков Г.М. Чисельные методы електронный вариант учебника. 5. Белашов В. Ю., Чернова Н. М. Эффективные алгоритмы и программы вычислительной математики. Магадан: СВКНИИДВОРАН, 1997. 160 с. 6. Культін Н.Б. Программирование в Turbo Pascal 7.0 и Delphi. – СПб: BHV- Санкт-Петербург, 1999. – 234с. ДОДАТОК А ТЕКСТ ПРОГРАМИ МОВОЮ Microsoft Visual C++ MainFrm.cpp #include "StdAfx.h" #include "example.h" #include "MainFrm.h" #ifdef _DEBUG #define new DEBUG_NEW #undef THIS_FILE static char THIS_FILE[] = __FILE__; #endif IMPLEMENT_DYNCREATE(CMainFrame, CFrameWnd) BEGIN_MESSAGE_MAP(CMainFrame, CFrameWnd) END_MESSAGE_MAP() static UINT indicators[] = { ID_SEPARATOR, ID_INDICATOR_CAPS, ID_INDICATOR_NUM, ID_INDICATOR_SCRL, }; CMainFrame::CMainFrame() { } CMainFrame::~CMainFrame() { } int CMainFrame::OnCreate(LPCREATESTRUCT lpCreateStruct) { if (CFrameWnd::OnCreate(lpCreateStruct) == -1) return -1; if (!m_wndToolBar.Create(this) || !m_wndToolBar.LoadToolBar(IDR_MAINFRAME)) { TRACE0("Failed to create toolbar\n"); return -1; } if (!m_wndStatusBar.Create(this) || !m_wndStatusBar.SetIndicators(indicators, sizeof(indicators)/sizeof(UINT))) { TRACE0("Failed to create status bar\n"); return -1; }
m_wndToolBar.SetBarStyle(m_wndToolBar.GetBarStyle() | CBRS_TOOLTIPS | CBRS_FLYBY | CBRS_SIZE_DYNAMIC); m_wndToolBar.EnableDocking(CBRS_ALIGN_ANY); EnableDocking(CBRS_ALIGN_ANY); DockControlBar(&m_wndToolBar); return 0; } BOOL CMainFrame::PreCreateWindow(CREATESTRUCT& cs) { return CFrameWnd::PreCreateWindow(cs); } #ifdef _DEBUG void CMainFrame::AssertValid() const { CFrameWnd::AssertValid(); } void CMainFrame::Dump(CDumpContext& dc) const { CFrameWnd::Dump(dc); } #endif MainFrm.h #if!defined(AFX_MAINFRM_H__9A49CF0A_0006_11D3_A7F6_F5D97F5F2E6D__INCLUDED_) #define AFX_MAINFRM_H__9A49CF0A_0006_11D3_A7F6_F5D97F5F2E6D__INCLUDED_ #if _MSC_VER >= 1000 #pragma once #endif class CMainFrame : public CFrameWnd { protected: CMainFrame(); DECLARE_DYNCREATE(CMainFrame) public: // Operations public: // Overrides // ClassWizard generated virtual function overrides //{{AFX_VIRTUAL(CMainFrame) virtual BOOL PreCreateWindow(CREATESTRUCT& cs); //}}AFX_VIRTUAL // Implementation public: virtual ~CMainFrame(); #ifdef _DEBUG virtual void AssertValid() const; virtual void Dump(CDumpContext& dc) const; #endif protected: // control bar embedded members CStatusBar m_wndStatusBar; CToolBar m_wndToolBar; // Generated message map functions protected: //{{AFX_MSG(CMainFrame) afx_msg int OnCreate(LPCREATESTRUCT lpCreateStruct); // afx_msg void OnDemoAnalit(); //}}AFX_MSG DECLARE_MESSAGE_MAP() }; ///////////////////////////////////////////////////////////////////////////// //{{AFX_INSERT_LOCATION}} // Microsoft Developer Studio will insert additional declarations immediately before the previous line. #endif //!defined(AFX_MAINFRM_H__9A49CF0A_0006_11D3_A7F6_F5D97F5F2E6D__INCLUDED_) StdAfx.h // stdafx.h : include file for standard system include files, // or project specific include files that are used frequently, but // are changed infrequently // #if!defined(AFX_STDAFX_H__9A49CF08_0006_11D3_A7F6_F5D97F5F2E6D__INCLUDED_) #define AFX_STDAFX_H__9A49CF08_0006_11D3_A7F6_F5D97F5F2E6D__INCLUDED_ #if _MSC_VER >= 1000 #pragma once #endif // _MSC_VER >= 1000 #define VC_EXTRALEAN // Exclude rarely-used stuff from Windows headers #include <afxwin.h> // MFC core and standard components #include <afxext.h> // MFC extensions #include <afxdisp.h> // MFC OLE automation classes #ifndef _AFX_NO_AFXCMN_SUPPORT #include <afxcmn.h> // MFC support for Windows Common Controls #endif // _AFX_NO_AFXCMN_SUPPORT //{{AFX_INSERT_LOCATION}} // Microsoft Developer Studio will insert additional declarations immediately before the previous line. #endif //!defined(AFX_STDAFX_H__9A49CF08_0006_11D3_A7F6_F5D97F5F2E6D__INCLUDED_) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
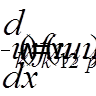
 ,
, , в якій додаткові умови накладаються на значення функцій
, в якій додаткові умови накладаються на значення функцій 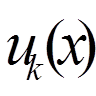 більше ніж в одній точці цього відрізка. Очевидно, що крайові
задачі можливі для систем порядку не нижче другого.
більше ніж в одній точці цього відрізка. Очевидно, що крайові
задачі можливі для систем порядку не нижче другого.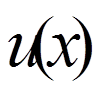 навантаженої струни із закріпленими кінцями
навантаженої струни із закріпленими кінцями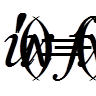 ,
, 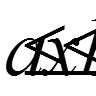 ,
, 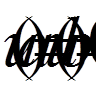 ;
(1)
;
(1)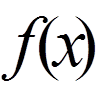 - зовнішнє
згинаюче навантаження на одиницю довжини струни, поділене на пружність струни.
- зовнішнє
згинаюче навантаження на одиницю довжини струни, поділене на пружність струни.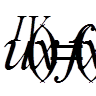 ,
, 

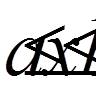 ; (2)
; (2)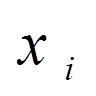 ,
, 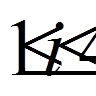 , на опорах, то
додаткові умови мають вид
, на опорах, то
додаткові умови мають вид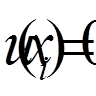 ,
, 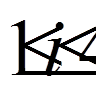 ,
, 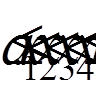 ,
,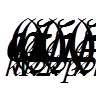 ,
,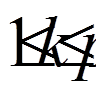 ,
, 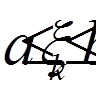 .
.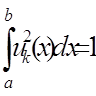 ,
,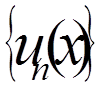 - повна система функцій з ненульовою нормою, ортогональних на
відрізку [a, b]. Якщо неперервна функція
- повна система функцій з ненульовою нормою, ортогональних на
відрізку [a, b]. Якщо неперервна функція 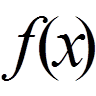 ортогональна на відрізку [a, b] до всіх функцій
ортогональна на відрізку [a, b] до всіх функцій 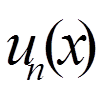 , тобто
, тобто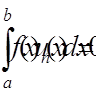 (n = 0, 1, 2, . .
.), (3)
(n = 0, 1, 2, . .
.), (3)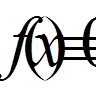 при
при 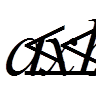
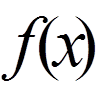 відносно заданої системи ортогональних
функцій
відносно заданої системи ортогональних
функцій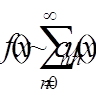 (4)
(4)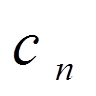 визначаються
за формулою
визначаються
за формулою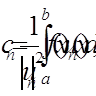 де
де 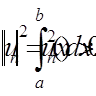
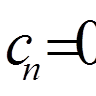 (n = 0, 1, 2, . . .). (5)
(n = 0, 1, 2, . . .). (5)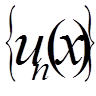 у відношенні до будь-якої неперервної функції
у відношенні до будь-якої неперервної функції 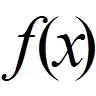 виконана рівність повноти
виконана рівність повноти 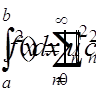 (6)
(6)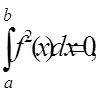
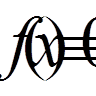 при
при 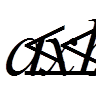
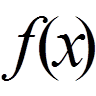
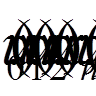 (тобто
(тобто 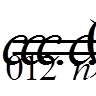 то
то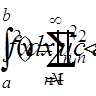
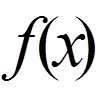 в середньому на відрізку [a, b] буде як
завгодно малою. При додаткових обмеженнях звідси випливає, що
в середньому на відрізку [a, b] буде як
завгодно малою. При додаткових обмеженнях звідси випливає, що 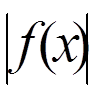 також малий на відрізку
також малий на відрізку 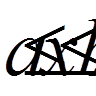
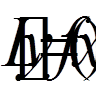 (7)
(7)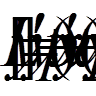 при наявності
лінійних крайових умов
при наявності
лінійних крайових умов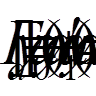
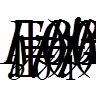 (8)
(8)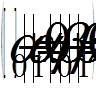
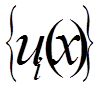 (
( = 0, 1, . , n), що складають
частину деякої повної системи, причому потурбуємося, щоб функція
= 0, 1, . , n), що складають
частину деякої повної системи, причому потурбуємося, щоб функція 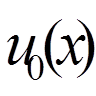 задовольняла неоднорідні крайові умови
задовольняла неоднорідні крайові умови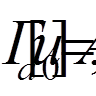
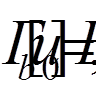
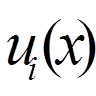 (
( = 1, 2, . . . , n) задовольняли б однорідним крайовим умовам
= 1, 2, . . . , n) задовольняли б однорідним крайовим умовам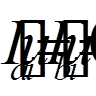 (
( = 1, 2, . . . , n).
= 1, 2, . . . , n).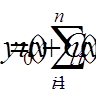 (9)
(9)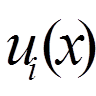 функція
функція 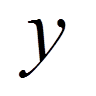 , що визначається формулою (9), очевидно,
задовольняє крайовим умовам (8) при будь-якому виборі
коефіцієнтів
, що визначається формулою (9), очевидно,
задовольняє крайовим умовам (8) при будь-якому виборі
коефіцієнтів 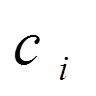 . Вираз (9) підставимо у
диференціальне рівняння (7), що дає
нев’язність
. Вираз (9) підставимо у
диференціальне рівняння (7), що дає
нев’язність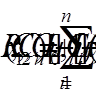
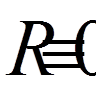 ; тому для отримання наближеного розв’язку, близького до точного,
нам вигідно підібрати коефіцієнти
; тому для отримання наближеного розв’язку, близького до точного,
нам вигідно підібрати коефіцієнти 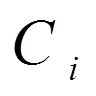 так, щоб функція
так, щоб функція 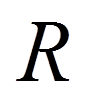 була в якомусь сенсі малою.
була в якомусь сенсі малою.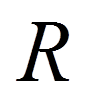 була ортогональною до базисних
функцій
була ортогональною до базисних
функцій  (
( = 1, 2, . . . , n), що при достатньо великому числі цих функцій, в силу наведеного вище зауваження, забезпечує малість нев’язності в середньому.
= 1, 2, . . . , n), що при достатньо великому числі цих функцій, в силу наведеного вище зауваження, забезпечує малість нев’язності в середньому.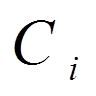 (
( = 1, 2, . . . , n) приходимо до системи лінійних рівнянь
= 1, 2, . . . , n) приходимо до системи лінійних рівнянь
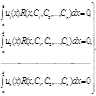
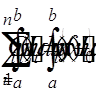 (10)
(10) = 1, 2, . . . , n).
= 1, 2, . . . , n). .
.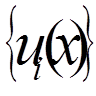 (
( = 0, 1, . . . , n) так, щоб функція
= 0, 1, . . . , n) так, щоб функція 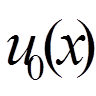 задовольняла крайовим умовам:
задовольняла крайовим умовам: 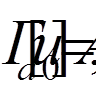
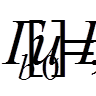 а функції
а функції 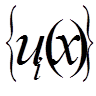 (
( = 1, 2, . . . , n) задовольняли б
однорідним крайовим умовам
= 1, 2, . . . , n) задовольняли б
однорідним крайовим умовам 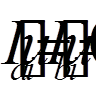 (
( = 1, 2, . . . , n).
= 1, 2, . . . , n).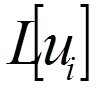 (
( = 0, 1, 2, 3, 4).
= 0, 1, 2, 3, 4).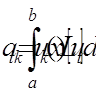 ,
, 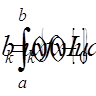
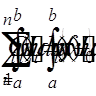 (
( = 1, 2, . . . , n).
= 1, 2, . . . , n).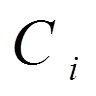 (
( = 1, 2, . . . , n) і отримуємо
розв’язок вигляді:
= 1, 2, . . . , n) і отримуємо
розв’язок вигляді: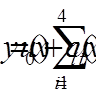 .
.
 Так
Так
 (
( =
0, 1, 2, 3, 4)
=
0, 1, 2, 3, 4)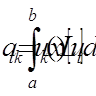 ,
,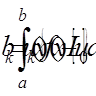
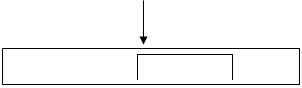


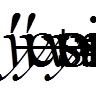 , (11)
, (11)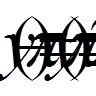 . (12)
. (12)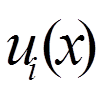 (
(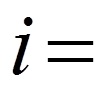 0, 1, 2, 3, 4) наступні тригонометричні
функції:
0, 1, 2, 3, 4) наступні тригонометричні
функції: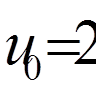 ,
, 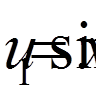 ,
, 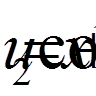 ,
, 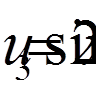 ,
, 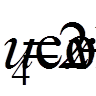 .
.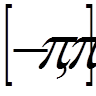 , причому функція
, причому функція 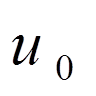 задовольняє крайовій умові (12), а інші
функції – нульовим крайовим умовам. Будемо шукати розв’язок у вигляді
задовольняє крайовій умові (12), а інші
функції – нульовим крайовим умовам. Будемо шукати розв’язок у вигляді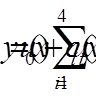 .
.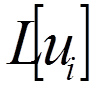 (
( = 0, 1, 2, 3, 4):
= 0, 1, 2, 3, 4):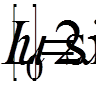 ,
, 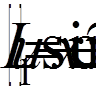 ,
, 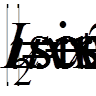 ,
, 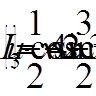 ,
, 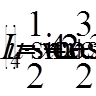 ,
, 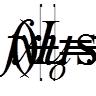 .
. 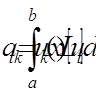 ,
, 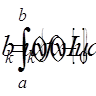 ,
,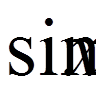 ,
, 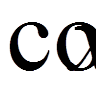 ,
, 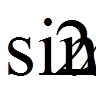 ,
, 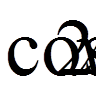 , . . .)
, . . .)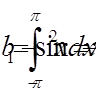 ,
,  ,
,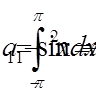 ,
, 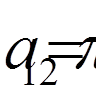 ,
, 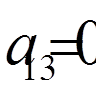 ,
, 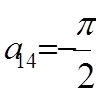 ,
,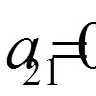 ,
, 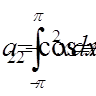 ,
, 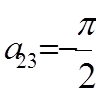 ,
, 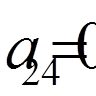 ,
,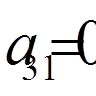 ,
, 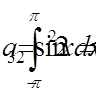 ,
, 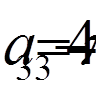 ,
, 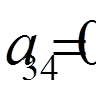 ,
,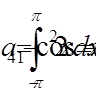 ,
, 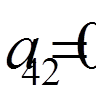 ,
, 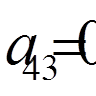 ,
, 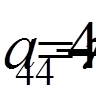 .
.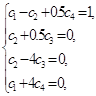
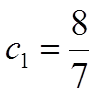 ,
, 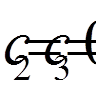 ,
, 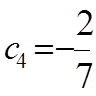 . Таким чином маємо
. Таким чином маємо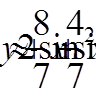 .
.