
|
Рефератыкосмонавтике административному праву хозяйственному праву устройствам экологическому праву криминалогия гражданский и землепользование обществознание |
Курсовая работа: Комплексные числа: их прошлое и настоящееКурсовая работа: Комплексные числа: их прошлое и настоящее
Комплексные числа, их прошлое и настоящее.
Содержание. I. Введение. II. Об истории возникновения комплексных чисел и их роли в процессе развития математики. III. Алгебраические действия над комплексными числами и их геометрический смысл. 1. Основные понятия и арифметические действия над комплексными числами. 2. Геометрическое изображение комплексных чисел. Тригонометрическая и показательная формы. 3. Операция сопряжения и ее свойства. 4. Извлечение корней. 5. Геометрический смысл алгебраических операций. IV. Применение комплексных чисел к решению алгебраических уравнений 3-ей и 4-ой степеней. 1. Формула Кердано. 2. Метод Феррари для уравнения 4-ой степени. V. Дополнительные задачи и упражнения, связанные с использованием комплексных чисел. VI. Заключение. VII. Литература. I. Введение. Алгебраические уравнения с одним неизвестным и связанные с ними вопросы в нахождении решений относятся к числу наиболее важных в школьной программе. В общем виде в средней школе изучаются лишь уравнения 1-ой степени (линейные) и уравнения 2-ой степени (квадратные), поскольку для таких уравнений существуют простые формулы, выражающие корни уравнения через его коэффициенты с помощью арифметических операций и извлечения корней. Именно, если дано: (α) Линейное уравнение ax+b=0, где а≠0, то x=-b/a – единственный корень; (β) Квадратное уравнение ax+bx+c=0, где a,b,c – действительные числа, a≠0, то x=-b±√b∙b-4ac/2a; при этом число корней зависит от величины D = b2 – 4ac, называемой дискриминантом квадратного уравнения, а именно: При D>0 – два действительных корня, D=0 – один двукратный корень (или, что то же, два совпадающих корня), D<0 – нет действительных корней. Из уравнений более высоких степеней в школьном курсе алгебры рассматриваются лишь некоторые частные их типы – трехчленные (например, биквадратные), симметрические, … Однако никаких методов для решения произвольных уравнений 3-ей и 4-ой степени (хотя соответствующие формулы известны), в школьной алгебре не дается, т.к. эти методы существенно опираются на теорию комплексных чисел. Цель данного реферата состоит в том, чтобы ознакомить учащихся средних школ с важнейшим и новым для них математическим понятием – понятием комплексного числа, а также показать, насколько эффективно его применение при решении некоторых задач, в том числе и в первую очередь, при решении кубичных уравнений. II. Об истории возникновения комплексных чисел и их роли в процессе развития математики. Комплексные числа возникли в математике в начале XVI века в связи с решением алгебраических уравнений 3-ей степени, а позднее, и уравнений 2-ой степени. Некоторые итальянские математики того времени (- Сципион дель Ферро, Николо Тарталья, Джироломо Кардано, Рафаэль Бомбелли) ввели в рассмотрение символ √-1 как формальное решение уравнения х2+1=0, а также выражение более общего вида (а+b∙√-1) для записи решения уравнения (х-а)2+b2=0. Впоследствии выражения вида (а+b∙√-1) стали называть «мнимыми», а затем «комплексными» числами и записывать их в виде (а+bi) (символ i для обозначения √-1 ввел Леонард Эйлер в XVIII в.). Этих чисел, чисел новой природы оказалось достаточно для решения любого квадратного уравнения (включая случай D < 0), а также уравнения 3-ей и 4-ой степени. МатематикиXVI в. и следующих поколений вплоть до начала XIXвека относились к комплексным числам с явным недоверием и предубеждением. Они считали эти числа «мнимыми» (Декарт), «несуществующими», «вымышленными», «возникшими от избыточного мудрствования» (Кардано)… Лейбниц называл эти числа «изящным и чудесным убежищем божественного духа», а √-1 считал символом потустороннего мира (и даже завещал начертать его на своей могиле). Однако использование аппарата комплексных чисел (несмотря на подозрительное к ним отношение), позволило решить многие трудные задачи. Поэтому со временем комплексные числа занимали все более важное положение в математике и ее приложениях. В первую очередь они глубоко проникали в теорию алгебраических уравнений, существенно упростив их изучение. Например, один из трудных вопросов для математиков XVII-XVIII веков состоял в определении числа корней алгебраического уравнения n-ой степени, т.е. уравнения вида a0∙xn+a1∙xn-1+…+an-1∙x+an=0. Ответ на этот вопрос, как оказалось, зависит от того, среди каких чисел – действительных или комплексных – следует искать корни этого уравнения. Если ограничиться действительными корнями, то можно лишь утверждать, что их не больше, чем n. А если считать допустимым наличие и комплексных решений, то ответ на поставленный вопрос получается исчерпывающий: любое алгебраическое уравнение степени n (n≥1) имеет ровно n корней (действительных или комплексных), если каждый корень считать столько раз, какова его кратность (а это – число совпадающих с ним корней). При n≥5 общее алгебраическое уравнение степени n неразрешимо в радикалах, т.е. не существует формулы, выражающей его корни через коэффициенты с помощью арифметических операций и извлечения корней натуральной степени. После того как в XIX в появилось наглядное геометрическое изображение комплексных чисел с помощью точек плоскости и векторов на плоскости (Гаусс в 1831 г, Вессель в 1799 г, Арган в 1806 г), стало возможным сводить к комплексным числам и уравнениям для них многие задачи естествознания, особенно гидро- и аэродинамики, электротехники, теории упругости и прочности, а также геодезии и картографии. С этого времени существование «мнимых», или комплексных чисел стало общепризнанным фактом и они получили такое же реальное содержание, как и числа действительные. К настоящему времени изучение комплексных чисел развилось в важнейший раздел современной математики – теорию функций комплексного переменного (ТФКП).
III/ Алгебраические действия над комплексными числами и их геометрический смысл.
1. Основные понятия и арифметические действия над комплексными числами. Логически строгую теорию комплексных чисел построил в XIX в (1835 г) ирландский математик Вильям Роумен Гамильтон. По Гамильтону комплексные числа – это упорядоченные пары z=(x,y) действительных чисел, для которых следующим образом определены операции сложения и умножения: (x1,y1)+(x2,y2)=(x1+x2, y1+y2); (1) (x1,y1)∙(x2,y2)=(x1∙x2 – yiy2, xiy2 + x2y1). (2) Действительные числа x и y называются при этом действительной и мнимой частями комплексного числа z=(x,y) и обозначаются символами Rez и Imz соответственно (real – действительный, imanginerum – мнимый). Два комплексных числа z1=(x1,y1) и z2=(x2,y2) называются равными только в том случае, когда x1=x2 и y1=y2. Из определения следует, что всякое комплексное число (x,y) может быть представлено в следующем виде: (x,y)=(x,0)+(0,1)(y,0). (3) Числа вида (х,0) отождествляются с действительными числами х, т.е. (х,0)=х, число (0,1), называемое мнимой единицей, обозначается символом i, т.е. (0,1)=i, причем i2=-1, равенство (3) принимает вид z=x+iy и называется алгебраической формой записи комплексного числа z=(x,y). Операции сложения и умножения комплексных чисел имеют следующие свойства: а) z1+z2=z2+z1 (переместительный закон или коммутативность сложения и умножения) б) z1z2=z2z1 в) z1+(z2+z3)=(z1+z2)+z3 (сочетательный закон или ассоциативность) г) z1(z2z3)=(z1z2)z3 д) (z1+z2)z3=z1z3+z2z3 (распределительный закон или дистрибутивность) Вычитание и деление комплексных чисел z1=x1+iy1 и z2=x2+iy2 определяют, причем однозначно, их разность z1-z2 и частное z1/z2 как решения соответствующих уравнений z+z2=z1 и zz2=z1 (при z2≠0). Отсюда следует, что разность и частное от деления z1 на z2 вычисляются по формулам: z1-z2=(x1-x2)+i(y1-y2), (4) z1/z2=(x1x2+y1y2)/(x22+y22) + i((y1x2-x1y2)/(x22+y22)) (5) Данное определение можно выразить в других терминах, а именно, вычитание – как действие, обратное сложению: z=z1+(-z2), где число (-z2) называется противоположным z2; деление – как действие, обратное умножению: z=z1(z2-1), где z2-1 – число, обратное для z2 (z2≠0). Таким образом, анализ определений и свойств арифметических операций над комплексными числами приводит к следующим выводам: - множество комплексных чисел (С) является
расширением множества R
действительных чисел, т.е. действительные числа содержатся как частный случай,
среди комплексных (точно так же как, например, целые числа содержатся среди
действительных); 2. Геометрическое изображение комплексных чисел. Тригонометрическая и показательная формы. Замечание. Понятия «больше» или «меньше» для комплексных чисел лишено смысла (не принято никакого соглашения). Если на плоскости введена декартова система координат 0xy, то всякому комплексному числу z=x+iy может быть поставлена в соответствие некоторая точка М(х,у) с абсциссой «х» и ординатой «у», а также радиус – вектор 0М. При этом говорят, что точка М(х,у) (или радиус – вектор 0М) изображает комплексное число z=x+iy. Плоскость, на которой изображаются комплексные числа называется комплексной плоскостью, ось 0у – мнимой осью. Число r=√x2+y2, равное длине вектора, изображающего комплексное число, т.е. расстоянию от начала координат до изображающей это число точки, называется модулем комплексного числа z=x+iy и обозначается символом |z|. Угол φ=(0М,ˆ0х) между положительным направлением оси 0х и вектором 0М, изображающим комплексное число z=x+iy ≠0, называется его аргументом.
Из определения видно, что каждое комплексное число (≠0), имеет бесконечное множество аргументов. Все они отличаются друг от друга на целые кратные 2π и обозначаются единым символом Argz (для числа z=0 аргумент не определяется, не имеет смысла). Каждое значение аргумента совпадает с величиной φ некоторого угла, на который следует повернуть действительную ось (ось 0ч) до совпадения ее направления с направлением радиус-вектора точки М, изображающей число z (при этом φ > 0, если поворот совершается против часовой стрелки и φ <0 в противном случае). Таким образом, аргумент комплексного числа z=x+iy ≠0 есть всякое решение φ системы уравнений cosφ=x/√x2+y2; sinφ=y/√x2+y2. Значение Argz при условии 0≤Argz<2π называется главным значением аргумента и обозначается символом argz. В некоторых случаях главным значением аргумента считают наименьшее по абсолютной величине его значения, т.е. значение, выделяемое неравенством -π<φ≤π. Между алгебраическими х, у и геометрическими r, φ характеристиками комплексного числа существует связь, выражаемая формулами x=rcosφ, y=rsinφ, следовательно, z=x+iy=r(cosφ+isinφ). Последнее выражение, т.е. z= r(cosφ+isinφ) (6) называется тригонометрической формой комплексного числа. Любое число z≠0 может быть представлено в тригонометрической форме. Для практики число вида (cosφ+isinφ) удобнее записывать короче, с помощью символа eiφ=cosφ+isinφ (7). Доказанное для любых чисел φ (действительных или комплексных) это равенство называется формулой Эйлера. С ее помощью всякое комплексное число может быть записано в показательной форме z=reiφ (8) 3. Операция сопряжения и ее свойства. Для данного комплексного числа z=x+iy число x-iy (отличающееся от z лишь знаком при мнимой части) называется сопряженным и обозначается символом z. Переход от числа z к числу z называется сопряжением, а сами эти числа сопряженными (друг к другу), т.к. (z)=z. Из определения следует, что только действительное число сопряжено самому себе. Геометрически сопряженные числа изображаются точками, симметричными относительно действительной оси (рис.2).
Отсюда следует, что |z|=|z|, argz=-argz. Кроме того,
z-z=2iy=2iImz; zz=x2+y2=|z|2, а также: z1+z2=z1+z2; z1z2=z1z2; (z1/z2)=z1/z2; P(z)=P(z), где Р (z) – любой многочлен с действительными коэффициентами; (P(z)/Q(z))=(P(z)/Q(z)), где P и Q – многочлены с действительными коэффициентами. 4. Извлечение корней. Извлечение корня из комплексного числа есть действие, обратное возведению в степень. С его помощью по данной степени (подкоренное число) и данному показателю степени (показатель корня) находят основание (корень). Иначе говоря, это действие равносильно решению уравнения zn=a для нахождения z. В множестве комплексных чисел действие извлечения корня всегда выполнимо, хотя причем и неоднозначно: в результате получается столько значений, каков показатель корня. В частности, квадратный корень имеет ровно два значения, которые можно найти по формуле: √a=√α+iβ=±((√|a|+α)/2 ± i(√|a|-α)/2)), где знак «+» в скобках берется при β>0, «-» - при β<0. 5. Геометрический смысл алгебраических операций. Пусть даны два комплексных числа z1 и z2. В результате сложения этих чисел получается число z3, изображаемое вектором 0С диагонали параллелограмма 0АСВ (по правилу параллелограмма сложения векторов): z1+z2=0A+0B=0C=z3.
Разность (z1-z2) данных чисел, соответствующая их вычитанию, можно рассматривать как сумму вектора 0А, изображающего число z1 и вектора 0D=--0В, противоположного вектору 0В (симметричного ему относительно начала координат): z1-z2=z1+(-z2)=0A+0D=0E=BA. Таким образом, разности (z1-z2) данных чисел соответствует вектор ВА другой диагонали параллелограмма 0АСВ. Для иллюстрации остальных алгебраических действий над комплексными числами более удобна тригонометрическая форма. Умножение. Пусть даны два комплексных числа z1=r1(cosφ1+isinφ1) и z2=r2(cosφ2+isinφ2). Перемножая их получим z1z2=r1r2(cos(φ1+φ2)+isin(φ1+φ2)). Следовательно, при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Это правило верно и для любого числа сомножителей. Деление. Если требуется разделить z1 на z2, то выполняем следующие преобразования: z1/z2=(z1z2)/(z2z2)=(r1(cosφ1+isinφ1)r2(cosφ2-isinφ2))/ (r2(cosφ2+isinφ2)r2(cosφ2-isinφ2))=(r1/r2)(cos(φ1-φ2)+isin(φ1-φ2)), т.е. при делении двух комплексных чисел их модули делятся, а аргументы вычитаются. Возведение в степень. Умножая число z=r(cosφ+isinφ) само на себя «n» раз, получаем согласно правилу умножения zn=rn(cosφ+isinφ)n=rn(cosnφ+isinnφ). Таким образом, при возведении комплексного числа в степень «n» в ту же степень возводимся его модуль, а аргумент умножается на «n» (на показатель степени). В частном случае, если r=1, то предыдущее равенство принимаем вид (cosφ+isinφ)n= cosnφ+isinnφ (9). Полученная формула называется формулой Муавра (1667-1754). Извлечение корня. Пусть а=reiφ, z=ρeiσ. Решаем уравнение zn=a для вычисления n√a: ρneinσ=reiφ. Отсюда с учетом того, что аргументы чисел отличаются на целое кратное числу 2π, получаем: ρn=r, nσ-φ=2πK, или ρ=n√r; σK+1=(φ+2πK)/n (причем К=0,1,2…n-1). Таким образом, zk=n√r(cosφ+isinφ)=n√r((cosφ+2Kπ)/n+isin(φ+2Kπ)/n)) (10), где n√r , - арифметический корень, а К=0,1,2,…,n-1; т.е. корень степени n в множестве комплексных чисел имеет “n” различных значений zk (исключение представляет z=0. В этом случае все значения корня равны между собой и равны нулю). Заметим также, что разность между аргументами соседних чисел zk+1 и zk постоянна и равна 2π/n: σk+1-σk=(φ+2π(K+1))/n-(φ+2πK)/n=2π/n. Отсюда следует, что все значения n√a располагаются на комплексной плоскости в вершинах некоторого правильного n-угольника с центром в начале координат.
IV. Применение комплексных чисел к решению алгебраических уравнений 3-ей и 4-ой степеней. 1. Формула Кардано. Рассмотрим приведенное алгебраическое уравнение 3-ей степени: x3+ax2+bx+c=0 (11). (общее уравнение 3-ей степени сводится к приведенному делением на коэффициент при старшей степени). С помощью замены x=y-a/3 это уравнение примет вид y3+py+q=0 (11’), где p и q – новые коэффициенты, зависящие от a,b,c. Пусть у0 – какой либо корень уравнения (11’). Представим его в виде у0=α+β, где α и β – неизвестные пока числа, и подставим в уравнение. Получим α3+β3+( α+β)(3αβ+p)+q=0 (12). Выберем теперь α и β так, чтобы 3αβ+р=0. Такой выбор чисел α и β возможен, т.к. они (вообще говоря комплексные) удовлетворяют системе уравнений
αβ=-р/3, а значит, существуют. При этих условиях уравнение (12) примет вид α3+β3+q=0, а т.к. еще α3β3=-р3/27, то получаем систему
α3β3=-р3/27, из которой по теореме Виета следует, что α3 и β3 являются корнями уравнения t2+qt-p3/27=0. Отсюда находим: α3=-q/2+√q2/4+p3/27; β3=-q/2-√q2/4+p3/27, где √q2/4+p3/27 означает одно из возможных значений квадратного корня. Отсюда следует, что корни уравнения (11’) выражаются формулой D=(q/2)2+(p/3)3. y1.2.3=n√-q/2+√q2/4+p3/27+3√-q/2-√q2/4+p3/27, причем для каждого из трех значение первого корня 3√α соответствующие значения второго корня 3√β нужно брать так, чтобы было выполнено условие αβ=-р/3. Полученная формула называется формулой Кардано (ее можно записать в более компактном виде у=3√α+3√β, где α=-q/2+√q2/4+p3/27; β=-q/2-√q2/4+p3/27. Подставив в нее вместо р и q их выражения через a,b,c и вычитая а/3, получим формулу для уравнения (11). 2. Метод Феррари для уравнения 4-ой степени. Рассмотрим приведенное уравнение 4-ой степени x4+ax3+bx2+cx+d=0 (13). Сделав замену переменной х=у-а/4, получим уравнение у4+ру2+qy+r=0 (14) c коэффициентами p,q,r, зависящими от a,b,c,d. Преобразуем это уравнение к виду (y2+p/2)2+qy+(r-p2/4)=0, а затем, введя произвольное пока число α, представим его левую часть в равносильной форме (y2+p/2+α)2-[2α(y2+p/2)+α2-qy+p2/4-r]=0 (15) Выберем теперь число α так, чтобы выражение в квадратных скобках 2αy2-qy+(αp+α2+p2/4-r) стало полным (точным) квадратом относительно у. Для этого нужно, чтобы его дискриминант был равен нулю, т.е. чтобы q2-8α(αp+α2+p2/4-r)=0, или 8α3+8pα2+8α(p2/4-r)-q2=0. Таким образом, для нахождения α получается уравнение 3-ей степени, и задача сводится к предыдущей. Если в качестве «α» взять один из корней этого уравнения, то левая часть уравнения (15) будет разностью квадратов и поэтому может быть разложена в произведение двух многочленов 2-ой степени относительно «у». V. Дополнительные задачи и упражнения, связанные с использованием комплексных чисел. 1. Вычислить: ii2i3…i10=? Решение: ii2i3…i10=i1+2+…+10=i11∙10/2=i55=ii54=i(i2)27=i(-1)27=-i. 2. Каков геометрический смысл выражений: а) |z|, б)Argz; в) |z1-z2|, г) Arg(z1/z2)? Ответ: а) расстояние от начала координат до точки, изображающей комплексное число z; б) угол, на который нужно повернуть действительную ось до совпадения с направлением вектора 0М, изображающего комплексное число z; в) |z1-z2|- расстояние между точками z1 и z2, изображающими комплексные числа z1 и z2; г) Arg(z1/z2) – угол между изображающими векторами 0z1 и 0z2. 3. Доказать, что cos3φ=cos3φ-3sin2φcosφ; sin3φ=3cos2φsinφ-sin3φ.
4. Найти действительные решения уравнения (3+i)x+(-5+2i)y=4+16i.
x+2y=16 x=8; y=4. Ответ: z=8+4i. 5. Доказать тождество |z1+z2|2+|z1-z2|2=2(|z1|2+|z2|2) и вычислить его геометрический смысл. Доказательство: |z1+z2|2+|z1-z2|2= (z1+z2)( z1+z2)+( z1-z2)( z1-z2)= (z1+z2)( z1+z2)+ +( z1-z2)( z1-z2)=2 z1 z1+2 z2 z2=2(|z1|2+|z2|2). Геометрический смысл: сумма квадратов длин диагоналей равна сумме квадратов всех сторон параллелограмма. 6. Найти геометрическое место точек: а) |z-z0|=R; б) z=z0+Reit (0≤t<2π) Ответ: Окружность радиуса R с центром в z0.
г) |z+i|=|z-3|=|z-1-i|;
π/4≤argz≤5π/4 Решение: в) точка z должна быть удалена на такое же расстояние от точки z1=-2, как и от точки z2=3i, т.е. должна находиться на серединном перпендикуляре, проведенном к отрезку АВ. Следовательно, искомое геометрическое место точек – это прямая, проходящая через точку С (хс;ус), где хс=(-2+0)/2=-1; ус=(3+0)/2=3/2, перпендикулярная отрезку АВ.
7. Доказать тождество: (2x-z)2+(2x-z)2=2Re(z2). Доказательство: 1) (2x-z)2+(2x-z)2= 4x2-4xz+z2+4x2-4xz+z2=8x2-4x(z+z)+z2+z2=8x2-4x2x+(z+z)2- -2zz=(2x)2-2|z|2=4x2-2(x2+y2)=2(x2+y2)=2Re(z2). 2) 2Re(z2)=2Re(x+iy)2=2Re(x2-y2+2ixy)=2(x2-y2). 8. Решить систему уравнений
(4+2i)z1+(2+3i)z2=7. Решение: Применим правило Крамера:
(4+2i)+(2+3i)
7 (2+3i)
(4+2i) 7
21+23i 21+23i 21+23i Ответ: z1=1; z2=-i. 9. Доказать, что (а2+1)(b2+1)(c2+1) можно представить в виде суммы квадратов целых чисел (a,b,c – целые числа). Доказательство: заметим, что а2+1=|a+i|2, тогда имеем: (а2+1)(b2+1)(c2+1)=(a+i)(a-i)(b+i)(b-i)(c+i)(c-i)=(a+i)(b+i)(c+i)(a+i)(b+i)(c+i)= =((ab-1)+i(a+b))(c+i)((ab-1)+i(a+b))(c+i)=(((ab-1)c-a-b)+i((a+b)c+ab-1))((ab-1)c-a-b+i((a+b)c+ab-1)=(abc-(a+b+c))2+(ab+bc+ca-1)2. 10. Найти суммы: С=cosφ+cos2φ+…+cosnφ; S=sinφ+sin2φ+…+sinnφ. Решение: найдем сумму σ=с+iS=(eiφ+e2iφ+…+einφ) и выделим действительную и мнимую ее части, т.е. С=Reσ; S=Imσ. Последовательно имеем: eiφ+e2iφ+…+einφ= eiφ((1- einφ)/(1- eiφ))= (eiφ(1- einφ) (1- e-iφ))/( (1- eiφ) (1- e-iφ))= =(eiφ-1- eiφ(n+1)+ einφ)/|1- eiφ|2. Поскольку |1- eiφ|2=|(1-cosφ)-isinφ|2=(1-cosφ)2+sin2φ=4sin2(φ/2); Re(eiφ-1- eiφ(n+1)+ einφ)= cosφ-1-cos(n+1)φ+cosnφ= =- 2sin2(φ/2)+2sin(φ/2)sin(nφ+φ/2)= 2sin(φ/2)2sin(nφ/2)cos((n+1)φ)/2 и Im(eiφ-1- eiφ(n+1)+ einφ)=sinφ-sin(n+1)φ+sinnφ=2sin(φ/2)(cos(φ/2)-cos(nφ+φ/2))= =2sin(φ/2)2sin(nφ/2)sin(((n+1)φ)/2), то С=(4sin(φ/2)sin(nφ/2)cos(((n+1)φ)/2))/(4sin2(φ/2)) = =[sin(nφ/2) cos(((n+1)φ)/2))]/ sin(φ/2); S=(4sin(φ/2)sin(nφ/2)cos(((n+1)φ)/2))/(4sin2(φ/2)) = =[sin(nφ/2) cos(((n+1)φ)/2))]/ sin(φ/2) 11. Найти сумму 1+eπcosπ+e2πcos2π+…+enπcosnπ. Решение: Рассмотрим функцию S(x)=1+excosx+e2xcos2x+…+enxcosnx и найдем ее значение при х=π. В свою очередь, при нахождении суммы S(x) перейдем к комплексным числам: σ(z)=1+ex+ix+e2x+i2x+…+enx+inx= 1+ex(1+i)+e2x(1+i)+…+enx(1+i)=(1-( ex(1+i))n+1)/(1- ex(1+i))= =1-ex(n+1)(1+i)/(1-ex(1+i))=((1-ex(n+1)(1+i))(1-ex(1-i))/((1-ex(1+i))(1-ex(1-i))) =(1- ex(n+1)(1+i)- ex(1-i)+ex(n+2+ni))/|1- ex(1+i)|2= =(1-e(n+1)xei(n+1)x-exe-ix+e(n+2)xexni)/(1-2excosx+e2x) т.к. S(x)=Reσ(z), то получаем формулу: S(x)=1+excosx+e2xcos2x+…+enxcosnx=(1-e(n+1)xcos(n+1)x+e(n+2)xcosnx-excosx)/(1-2excosx+e2x) Отсюда следует, что искомая сумма равна: S(π)=1+eπcosπ+e2πcos2π+…+enπcosnπ= (1+eπ+eπ(n+2)(-1)n-e(n+1)(-1)n+1)/(1+2eπ+e2π)= =((1+eπ)+(-1)neπ(n+1)(eπ+1))/(eπ+1)2=(1+(-1)neπ(n+1))/(1+eπ)
Доказательство:
Решение: z=4√1+i√3=4√a, где a=1+i√3. Т.к. а=r(cosφ+isinφ)=2(cosπ/3+isinπ/3), то zk=4√2(cos(π/3+2Kπ)/4+isin(π/3+2Kπ), где К=0,1,2,3. Получаем: Z0= 4√2(cosπ/12+isinπ/12); z1=4√2(cos7π/12+isin7π/12); Z2=4√2(cos13π/12+isin13π/12); z4=4√2(cos19π/12+isin19π/12). 14. Представить в алгебраической форме комплексное число 1/(1+i√3)6-1/(√3-i)6 =z Решение: преобразуем данное число: Z=((1-i√3)/((1+i√3)(1-i√3)))6-((√3+i)/((√3-i)(√3+i)))6= =(1-i√3)6/|1+i√3|12-(√3+i)6/|√3+i|12=z1-z2=(т.к. |z1|=|z2|=2; φ1=-π/3; φ2=π/6, то)=1/26∙26(cos(-π/3)+isin(-π/3))6-1/26∙26(cosπ/6+isinπ/6))6= =cos(-2π)+isin(-2π)-cosπ-isinπ=1-(-1)=2.
VII. Литература. VIII. 1. Кураш А.Г. «Алгебраические уравнения произвольных степеней». М., «Наука», 1983. 2. Маркушевич А.И. «Комплексные числа и конформные отображения». М., «Физматгиз», 1960. 3. Стройк Д.Я. «Краткий очерк истории математики». М., «Наука», 1969. 4. Яглом И.И. « Комплексные числа и их применение в геометрии». М., Физматгиз, 1963. 5. Справочник по элементарной математике (для поступающих в ВУЗы) под редакцией Фильчакова П.Ф. «Наукова Думка», Киев – 1972. |
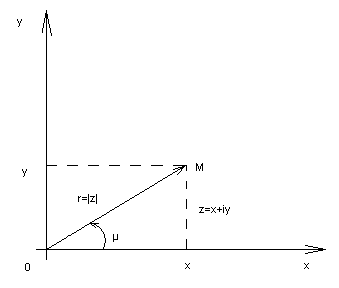
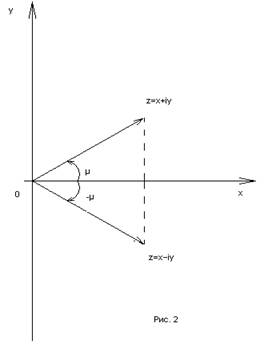
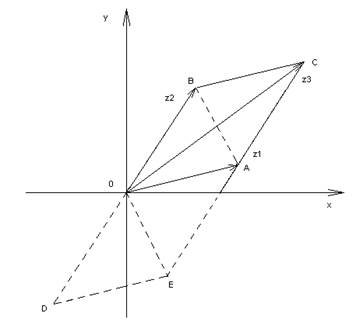 Рис.3
Рис.3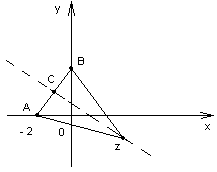 в) |z-3i|=|z+2|;
в) |z-3i|=|z+2|;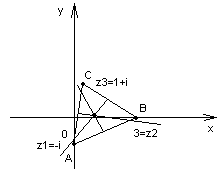 г) Рассматривая попарно
направленные равенства |z+i|=|z-3|
и |z-3|=|z-1-i|,
приходим к заключению, что искомое множество точек – это множество точек
пересечения серединных перпендикуляров, проведенных к отрезкам АВ и ВС (а также
и к АС).
г) Рассматривая попарно
направленные равенства |z+i|=|z-3|
и |z-3|=|z-1-i|,
приходим к заключению, что искомое множество точек – это множество точек
пересечения серединных перпендикуляров, проведенных к отрезкам АВ и ВС (а также
и к АС).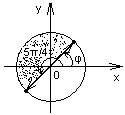 д) Верхний полукруг,
ограниченный лучами argz=π/4 и argz=5π/4
и окружностью |z|=R, не содержащий (∙)
z=0.
д) Верхний полукруг,
ограниченный лучами argz=π/4 и argz=5π/4
и окружностью |z|=R, не содержащий (∙)
z=0.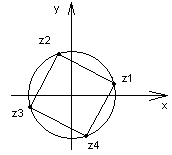 13. Найти все значения
корня 4√1+i√3.
Дать геометрическую иллюстрацию.
13. Найти все значения
корня 4√1+i√3.
Дать геометрическую иллюстрацию.