Геометрия – это наука о свойствах геометрических фигур. Слово «геометрия» греческое, в переводе на русский язык означает «землемерие». Такое название этой науке было дано потому, что в древнее время главной целью геометрии было измерение расстояний и площадей на земной поверхности.

Легко представить себе поверхность как границу тела: плоская поверхность стола, сферическая поверхность мяча, цилиндрическая поверхность трубы. Но такое представление не полно. Возьмем тонкую замкнутую проволоку изогнутой формы и опустим её в мыльную пену. Если мы осторожно извлечем её из пены, то увидим, что просвет в проволочном "кольце" затянут тончайшей мыльной пленкой. Правильно представлять себе поверхность именно как тонкую пленку (но лишенную всякой толщины).

Важнейшая и простейшая поверхность - плоскость. Прямая m, лежащая в плоскости, разбивает её на две части - полуплоскости; точки этой прямой и только они являются общими точками обеих полуплоскостей. Если А - точка одной полуплоскости, а В - другой, то отрезок АВ пересекает границу m полуплоскостей в некоторой точке С, лежащей между А и В.

Плоскости задаются тремя точками и обозначаются часто так: плоскость АВС или PQR и т.д. Иногда бывает проще обозначать плоскость одной буквой греческого алфавита: a, b, g, d...

Под фигурой обычно понимают некоторое сочетание определенным образом расположенных в одной плоскости (а иногда и в пространстве) элементов: точек, прямых, лучей, отрезков (иногда и плоскостей).

Под телом понимают обычно часть пространства, ограниченную какой-либо замкнутой поверхностью. Так, конус - тело, ограниченное канонической поверхностью с боков и плоским круглым основанием снизу. Куб - тело, ограниченное шестью квадратными гранями, и т.д. Курс геометрии традиционно подразделяется на планиметрию и стереометрию; в планиметрии рассматриваются свойства различных фигур (треугольников, многоугольников, окружностей), лежащих в плоскости. В стереометрии изучаются свойства пространственных фигур и тел.

1. Определение геометрического места точек

Геометрическое место точек – это множество всех точек, удовлетворяющих определённым заданным условиям.

Пример 1. Срединный перпендикуляр любого отрезка есть геометрическое место точек (т.е. множество всех точек), равноудалённых от концов этого отрезка. Пусть PO AB и AO = OB:

Тогда, расстояния от любой точки P, лежащей на срединном перпендикуляре PO, до концов A и B отрезка AB одинаковы и равны d. Таким образом, каждая точка срединного перпендикуляра отрезка обладает следующим свойством: она равноудалена от концов отрезка.

Пример 2. Окружность - это геометрическое место точек (т.е. множество всех точек), равноудалённых от её центра (одна из этих точек – А).

Тогда отрезок, соединяющий центр окружности с какой-либо её точкой, называется радиусом и обозначается r или R. Часть плоскости, ограниченная окружностью, называется кругом. Часть окружности AmB, называется дугой. Прямая PQ, проходящая через точки M и N окружности, называется секущей, а её отрезок MN, лежащий внутри окружности - хордой. Хорда, проходящая через центр круга например, BC называется диаметром и обозначается d или D. Диаметр – это наибольшая хорда, равная двум радиусам (d = 2r). Предположим, дана точка А (7; 3; 5); эта запись означает, что точка А определяется координатами х = 7, у = 3, z = 5. Если масштаб для построения чертежа задан или выбран, то откладывают на оси х от некоторой точки О отрезок ОАХ, равный 7 единицам, и на перпендикуляре к этой оси, проведенном из точки Ах, отрезки АХА' = 3 ед. и АХА" = 5 ед. Получаем проекции А' и А". Для построения достаточно взять только ось х. Принимая оси проекций за оси координат, можно найти координаты точки по данным ее проекциям. Например, отрезок ОАХ - выражает абсциссу точки А, отрезок АХА' - ее ординату, отрезок АХА" - аппликату. Если задается лишь абсцисса, то этому соответствует плоскость, параллельная плоскости, определяемой осями у и z. Действительно, такая плоскость является геометрическим местом точек, у которых абсциссы равны заданной величине. Если задаются две координаты, то этим определяется прямая, параллельная соответствующей координатной оси.

Например, имея заданными абсциссу и ординату, получаем прямую, параллельную оси z (это прямая АВ). Она является линией пересечения двух плоскостей _ и _, где _ - геометрическое место точек с равными ординатами. Прямая АВ служит геометрическим местом точек, у которых равны между собой абсциссы и равны между собой ординаты. Если задаются все три координаты, то этим определяется точка. Точка К, полученная в пересечении трех плоскостей, из которых _ есть геометрическое место точек по заданной абсциссе, _ - по заданной ординате и _ - по заданной аппликате. Точка может находиться в любом из восьми октантов. Следовательно, нужно знать не только расстояние данной точки от той или иной плоскости координат, но и направление, по которому надо это расстояние отложить; для этого координаты точек выражают относительными числами.

2. Сущность метода геометрических мест

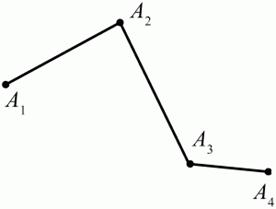
Сущность метода геометрических мест, используемого при решении задач, состоит в следующем. Пусть, решая задачу, нам надо найти точку X, удовлетворяющую двум условиям. Геометрическое место точек, удовлетворяющих первому условию, есть некоторая фигура F1, а геометрическое место точек, удовлетворяющих второму условию, есть некоторая фигура F2. Искомая точка X принадлежит F1 и F2 т. е. является их точкой пересечения. Если эти геометрические места простые (скажем, состоят из прямых и окружностей), то мы можем их построить и найти интересующую нас точку X.

Ломаной А1А2А3…An называется фигура, которая состоит из точек А1, А2, …, An и соединяющих их отрезков А1A2, A2A3, …, An-1, An. ТочкиА1, А2, …, Аn называются вершинами ломаной, а отрезки A1A2, A2A3, …, An-1, An – звеньями ломаной. Ломаная называется простой, если она не имеет самопересечений (рис. 1).

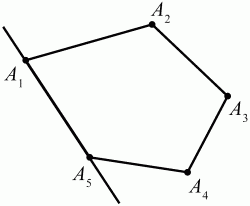
Рис. 1

А1A2A3A4 – простая ломаная из трёх звеньев.

Ломаная называется замкнутой, если у неё концы совпадают. Простая замкнутая ломаная называется многоугольником, если её соседние звенья не лежат на одной прямой. Вершины ломаной называются вершинами многоугольника, а звенья ломаной – сторонами многоугольника. Отрезки, соединяющие не соседние вершины многоугольника, называются диагоналями. Многоугольник с n-вершинами, а значит, и с n-сторонами называется n-угольником.

Плоским многоугольником и многоугольной областью называется конечная часть плоскости, ограниченная многоугольником.

Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону (рис. 2). Многоугольник называется невыпуклым, если он оказывается лежащим по обе стороны прямой, содержащей любую его сторону (рис. 3).

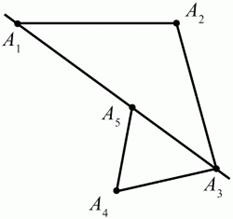
Рис. 2

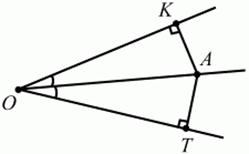
Рис. 3

Выпуклый многоугольник называют правильным, если у него все стороны равны, и все углы равны.

Многоугольник называется вписанным в окружность, если все его вершины лежат на некоторой окружности. Многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности.

Геометрия часто применяется на практике. Её надо знать и рабочему, и инженеру, и архитектору, и художнику. Одним словом, геометрию надо знать всем.

Планиметрия – это раздел геометрии, в котором изучаются фигуры на плоскости.

Фигура – это произвольное множество точек на плоскости. Точка, прямая, отрезок, луч, треугольник, круг, квадрат и так далее – всё это примеры геометрических фигур.

Основными геометрическими фигурами на плоскости являются точка и прямая. Этим фигурам в геометрии не даётся определений.

Также не определяются такие понятия (отношения), как «лежать между», «принадлежать», «проходить через…» и так далее.

Остальным геометрическим фигурам и другим понятиям даются определения. Определение – это предложение, в котором разъясняется смысл и содержание того или иного понятия. При этом разъяснение состоит в том, что оно сводится к ранее определённым понятиям.

Существует несколько подходов к построению курса планиметрии (и геометрии в целом): аксиоматический, аналитический, векторный, групповой.

Аксиоматическая теория строится следующим образом:

1) даются неопределяемые понятия (в нашем случае это точка и прямая);

2) вводятся неопределяемые отношения (связи между понятиями – «лежать между», «принадлежать» и так далее);

3) даётся система аксиом – то есть утверждений, принимаемых без доказательства;

4) на основе аксиом и законов математической логики доказываются теоремы.

Аксиом, как правило, немного, а вот теорем – бесконечное множество. К аксиомам планиметрии можно отнести следующие:

1. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

Через любые две точки можно провести прямую, и только одну.

2. Из трёх точек на данной прямой одна и только одна лежит между двумя другими.

3. Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин его частей, на которые он разбивается любой его точкой.

4. Прямая разбивает плоскость на две полуплоскости.

5. Каждый угол имеет определённую градусную меру, большую нуля. Развёрнутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

6. На любом луче от его начальной точки можно отложить отрезок заданной длины, и только один.

7. От любого луча в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.

8. Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данного луча.

9. Через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.

3. Основные геометрические места точек на плоскости

Геометрическим местом точек плоскости, равноудалённых от сторон угла, будет биссектриса данного угла (рис. 4). АК = AT, где А – любая точка на биссектрисе.

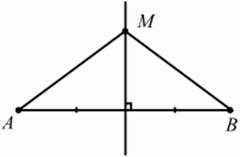
Рис. 4.

Геометрическим местом точек, равноудалённых от двух данных точек, будет прямая, перпендикулярная к отрезку, соединяющему эти точки, и проходящая через его середину (рис. 5). MA = MB, где М – произвольная точка на серединном перпендикуляре отрезка АВ.

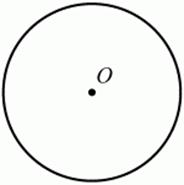
Рис. 5.

Геометрическим местом точек плоскости, равноудалённых от заданной точки, будет окружность с центром в этой точке (рис. 6). Точка О равноудалена от точек окружности.

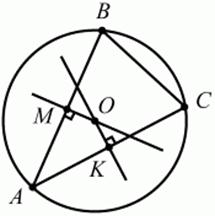
Рис. 6.

Местоположение центра окружности, описанной около треугольника.

Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведённых через середины этих сторон (рис. 7). А, В, С – вершины треугольника, лежащие на окружности.

АМ = МВ и АК = КС.

Точки М и К – основания перпендикуляров к сторонам АВ и АС соответственно.

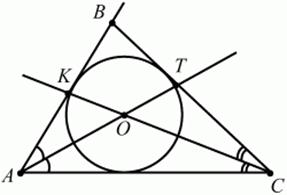
Рис. 7.

Местоположение центра окружности, вписанной в треугольник.

Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис (рис. 8). В ⊿ABC отрезки AT и СК являются биссектрисами.

Рис. 8.

4. Примеры задач на геометрические места точек

1. Два колеса радиусов r1 и r2 катаются по прямой l. Найдите множество точек пересечения M их общих внутренних касательных.

Решение :Пусть O1 и O2 — центры колес радиусов r1 и r2 соответственно. Если M — точка пересечения внутренних касательных, то O1M: O2M = r1: r2. Из этого условия легко получить, что расстояние от точки M до прямой l равно 2r1r2/(r1 + r2). Поэтому все точки пересечения общих внутренних касательных лежат на прямой, параллельной прямой l и отстоящей от нее на расстояние 2r1r2/(r1 + r2).

2. Найдите геометрическое место центров окружностей, проходящих через две данные точки.

Решение: Пусть окружность с центром O проходит через данные точки A и B. Поскольку OA = OB (как радиусы одной окружности), точка O лежит на серединном перпендикуляре к отрезку AB. Обратно, каждая точка O, лежащая на серединном перпендикуляре к AB, равноудалена от точек A и B. Значит, точка O — центр окружности, проходящей через точки A и B.

3. Стороны AB и CD четырехугольника ABCD площади S не параллельны. Найдите ГМТ X, лежащих внутри четырехугольника, для которых SABX + SCDX = S/2.

Решение: Пусть O — точка пересечения прямых AB и CD. Отложим на лучах OA и OD отрезки OK и OL, равные AB и CD соответственно. Тогда SABX + SCDX = SKOX + SLOX±SKXL. Следовательно, площадь треугольника KXL постоянна, т. е. точка X лежит на прямой, параллельной KL.

4. На плоскости даны точки A и B. Найдите ГМТ M, для которых разность квадратов длин отрезков AM и BM постоянна.

Решение: Введем систему координат, выбрав точку A в качестве начала координат и направив ось Ox по лучу AB. Пусть точка M имеет координаты (x, y). Тогда AM2 = x2 + y2 и BM2 = (x - a)2 + y2, где a = AB. Поэтому AM2 - BM2 = 2ax - a2. Эта величина равна k для точек M с координатами ((a2 + k)/2a, y); все такие точки лежат на прямой, перпендикулярной AB.

5. Дан прямоугольник ABCD. Найдите ГМТ X, для которых AX + BX = CX + DX.

Решение: Пусть l — прямая, проходящая через середины сторон BC и AD. Предположим, что точка X не лежит на прямой l, например что точки A и X лежат по одну сторону от прямой l. Тогда AX < DX и BX < CX, а значит, AX + BX < CX + DX. Поэтому прямая l — искомое ГМТ.

6. Даны две прямые, пересекающиеся в точке O. Найдите ГМТ X, для которых сумма длин проекций отрезков OX на эти прямые постоянна.

Решение: Пусть a и b — единичные векторы, параллельные данным прямым; x равен вектору ох . Сумма длин проекций вектора x на данные прямые равна |(a,x)| + |(b,x)| = |(a±b,x)|, причем смена знака происходит на перпендикулярах, восставленных из точки O к данным прямым. Поэтому искомое ГМТ — прямоугольник, стороны которого параллельны биссектрисам углов между данными прямыми, а вершины лежат на указанных перпендикулярах.

7. Даны окружность S и точка M вне ее. Через точку M проводятся всевозможные окружности S1, пересекающие окружность S; X — точка пересечения касательной в точке M к окружности S1 с продолжением общей хорды окружностей S и S1. Найдите ГМТ X.

Решение: Пусть A и B — точки пересечения окружностей S и S1. Тогда XM2 = XA . XB = XO2 - R2, где O и R — центр и радиус окружности S. Поэтому XO2 - XM2 = R2, а значит, точки X лежат на перпендикуляре к прямой OM.

8. Даны две непересекающиеся окружности. Найдите геометрическое место точек центров окружностей, делящих пополам данные окружности (т. е. пересекающих их в диаметрально противоположных точках).

Решение: Пусть O1 и O2 — центры данных окружностей, R1 и R2 — их радиусы. Окружность радиуса r с центром X пересекает первую окружность в диаметрально противоположных точках тогда и только тогда, когда r2 = XO12 + R12, поэтому искомое ГМТ состоит из таких точек X, что XO12 + R12 = XO22 + R22, все такие точки X лежат на прямой, перпендикулярной O1O2.

9. Внутри окружности взята точка A. Найдите геометрическое место точек пересечения касательных к окружности, проведенных через концы всевозможных хорд, содержащих точку A.

Решение:Пусть O — центр окружности, R — ее радиус, M — точка пересечения касательных, проведенных через концы хорды, содержащей точку A, P — середина этой хорды. Тогда OP * OM = R2 и OP = OA cos f, где f = AOP. Поэтому AM2 = OM2 + OA2 - 2OM * OA cos f = OM2 + OA2 - 2R2, а значит, величина OM2 - AM2 = 2R2 - OA2 постоянна. Следовательно, все точки M лежат на прямой, перпендикулярной OA.

10. Найдите геометрическое место точек M, лежащих внутри ромба ABCD и обладающих тем свойством, что AMD + BMC = 180o.

Решение: Пусть N — такая точка, что вектора MN = DA. Тогда NAM = DMA и NBM = BMC, поэтому четырехугольник AMBN вписанный. Диагонали вписанного четырехугольника AMBN равны, поэтому AM| BN или BM| AN. В первом случае AMD = MAN = AMB, а во втором случае BMC = MBN = BMA. Если AMB = AMD, то AMB + BMC = 180o и точка M лежит на диагонали AC, а если BMA = BMC, то точка M лежит на диагонали BD. Ясно также, что если точка M лежит на одной из диагоналей, то AMD + BMC = 180o.

11. а) Дан параллелограмм ABCD. Докажите, что величина AX2 + CX2 - BX2 - DX2 не зависит от выбора точки X.

б) Четырехугольник ABCD не является параллелограммом. Докажите, что все точки X, удовлетворяющие соотношению AX2 + CX2 = BX2 + DX2, лежат на одной прямой, перпендикулярной отрезку, соединяющему середины диагоналей.

Решение: Пусть P и Q — середины диагоналей AC и BD. Тогда AX2 + CX2 = 2PX2 + AC2/2 и BX2 + DX2 = 2QX2 + BD2/2, поэтому в задаче б) искомое ГМТ состоит из таких точек X, что PX2 - QX2 = (BD2 - AC2)/4, а в задаче a) P = Q, поэтому рассматриваемая величина равна (BD2 - AC2)/2.

Литература

1. Погорелов А.В. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. – М.: Просвещение, 2000, с. 61.

2. Савин А.П. Метод геометрических мест /Факультативный курс по математике: Учебное пособие для 7-9 классов средней школы. Сост. И.Л. Никольская. – М.: Просвещение, 1991, с. 74.

3. Смирнова И.М., Смирнов В.А. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2005, с. 84.

4. Шарыгин И.Ф. Геометрия. 7-9 классы: Учебник для общеобразовательных учебных заведений. – М.: Дрофа, 1997, с. 76.

5. Интернет ресурс: http://matschool2005.narod.ru/Lessons/Lesson8.htm