Контрольная работа: Метод потенциалов для решения транспортной задачи в матричной форме. Задача оптимального распределения ресурсов

Контрольная работа: Метод потенциалов для решения транспортной задачи в матричной форме. Задача оптимального распределения ресурсов

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

Факультет «Экономический»

Кафедра «Экономика, финансы и управление на транспорте»

КОНТРОЛЬНАЯ РАБОТА

по дисциплине: «ЭКОНОМИКО-МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ»

Воронеж 2008

Задача №1

Метод потенциалов для решения транспортной задачи в матричной форме с ограничениями пропускной способности.

Задание:

1.      Построить оптимальный план перевозок каменного угля с пяти станций Аi (i = 1,2,3,4,5), до девяти крупных потребителей, имеющих подъездные пути Вj (j = 1,2,…,9).

2.      Определить объем тонно-километровой работы начального и оптимального планов перевозки грузов.

Исходные данные (вариант 67):

Данные о наличии ресурсов на пяти станциях отправления Аi приведены в таблице 1, данные о размерах прибытия груза Вj на девять станций назначения – в таблице 2.

Таблица 1 - Ресурсы станций отправления Аi (строки матрицы)

Таблица 2 - Объем потребности Вj получателя (столбцы матрицы)

Решение:

Расстояние перевозки от каждой i–й станции отправления до каждой j–й станции назначения указано в правом верхнем углу каждой клетки матрицы. В левом верхнем углу ряда клеток матрицы указаны ограничения пропускной способности.

Условием задачи установлено, что размер всех ресурсов у отправителей равен общей потребности получателей:

С учетом полученных условий необходимо найти такие неотрицательные значения величин объемов перевозок хij, при которых сумма произведений значений критерия Сij на размер перевозок будет минимальной, т.е.

Первоначально строится начальный план базисного варианта способом наименьшего значения критерия.

Любой допустимый план является оптимальным тогда и только тогда, когда каждой строке и каждому столбцу матрицы могут быть присвоены некоторые числа Ui и Vj, называемые потенциалами и отвечающие условиям:

Vj – Ui ≤ Cij для хij = 0; (1)

Vj – Ui = Cij для dij > хij > 0; (2)

Vj – Ui ≥ Cij для хij = dij; (3)

где Vj – потенциал j–го столбца;

Ui – потенциал i–й строки;

Cij – расстояние перевозки от i–го поставщика до j–го потребителя;

хij – корреспонденция (размеры перевозок) от i–го поставщика до j–го потребителя;

dij – величина пропускной способности ij клетки.

Присвоение потенциалов начинают со строки, в которой среди базисных клеток имеется максимальное расстояние. Этой строке можно присвоить любой положительный потенциал, например, 100. Затем, используя условие оптимальности (2), находят потенциалы остальных строк и столбцов по формулам:

для j–го столбца

Vj = Ui + Cij;

для i–й строки

Ui = Vj – Cij.

Корреспонденция улучшения плана находится из следующего выражения:

хул = min [хij четн, (dij – хij)нечетн]

F(х) = 45·90 + 30·50 + 75·60 + 80·10 + 80·25 + 10·20 + 105·35 + 15·70 + 135·40 + 135·60 + 95·30 + 55·40 + 95·10 + 20·35 + 5·25 + 20·80 = 39700 ден. ед.

80 – 70 + 60 – 90 + 10 – 25 + 25 – 80 = – 90 < 0 – цикл подходит

r = {15; 45; 80; 20} =15

F(х) = 39700 – 90·15 = 38350 ден.ед.

30 – 90 + 10 – 25 + 25 – 80 + 80 – 35 = – 85 < 0 – цикл подходит

r = {30; 65; 5; 105} = 5

F(х) = 38350 – 85·5 = 37925 ден.ед.

90 – 25 + 10 – 90 + 30 – 35 = – 20 < 0 – цикл подходит

r = {60; 25; 100} = 25

План оптимальный.

F(х) = 37925 – 20·25 = 37425 ден.ед.

Ответ: F(х)нач. = 39700 ден.ед.; F(х)опт. = 37425 ден.ед.

Задача №2

Графический метод решения задачи оптимизации производственных процессов

Задание: Решить задачу линейного программирования графическим методом. Исходные данные (вариант 7):

Целевая функция: f(x) = x1 + 2x2 → max,

Ограничения: –x1 – x2 ≥ –1, x1– 2x2 ≤ 1.

Решение:

–х1 – х2 ≥ –1

х1 – 2х2 ≤ 1 (–1)

х1 ≥ 0; х2 ≥ 0

х1 + х2 ≤ 1

2х2 – х1 ≥ 1

х1 + х2 = 1

х1 = 1 – х2

Если х1 = 0, то х2 = 1;

если х2 = 0, то х1 = 1.

х1 – 2х2 = 1

х1 = 1 + 2х2

Если х1 = 0, то х2 = –1/2;

если х2 = 0, то х1 = 1.

Строим прямые уравнений ограничений и находим область допустимых решений (рис. 1).

х2 ≤ – х1 +1 – нижняя полуплоскость;

2х2 ≥ х1 –1 – верхняя полуплоскость.

Рис. 1 - Решением системы неравенств является т. С (0;1)

Ответ: х1= 0

х2 = 1

Задача №3

Применение симплекс-алгоритма для решения экономической оптимизированной задачи управления производством.

Исходные данные (вариант 7):

Целевая функция: f(x) = x1 + 2x2 –3х3 → max.

Ограничения: x1 + x2 + х3 = 25,

2x1 – 3x2 + 3х3 ≥ 10;

x1 – 3x2 + 4х3 ≤ 30.

Решение:

Т.к. дана задача на максимизацию целевой функции f, то она сводится к задаче на минимизацию функции –f.

Введем функцию q = –f = –x1 – 2x2 +3х3

От ограничений неравенств переходим к ограничениям-равенствам, введя новые переменные х4 и х5:

х4 = 2x1 – 3x2 + 3х3 – 10; х5 = –x1 + 3x2 – 4х3 + 30.

Получим следующую основную задачу линейного программирования:

x1 + x2 + х3 = 25

х4 = 2x1 – 3x2 + 3х3 – 10

х5 = –x1 + 3x2 – 4х3 + 30

 q = –x1 – 2x2 +3х3 → min

Выразим из 1-го уравнения х1 через другие неизвестные и подставим это его выражение в другие уравнения, а также в уравнение для функции q. Получим:

x1 = –x2 – х3 + 25

х4 = –2x2 – 2x3 + 50 –3х2 + 3х3 – 10

х5 = х2 + x3 – 25 + 3х2 – 4x3 + 30

q = x2 + х3 – 25 + 2х2 + 3x3

x1 = –x2 – х3 + 25 (1)

х4 = –5x2 + х3 + 40 (2)

х5 = 4х2 – 3x3 + 5 (3)

q = –x2 + 4х3 – 25 (4)

Выразим х2 из второго ограничения и подставим его выражение в первое и третье ограничения, а также в выражение для целевой функции:

5x2 = х3 – х4 + 40

х2 = 0,2х3 – 0,2х4 + 8

x1 = –0,2x3 + 0,2х4 – 8 –x3 + 25

х2 = 0,2х3 – 0,2х4 + 8

х5 = 0,8х3 – 0,8x4 + 32 –3x3 + 5

q = –0,2x3 + 0,2х4 – 8 + 4х3 – 25

x1 = –1,2x3 + 0,2х4 + 17

х2 = 0,2х3 – 0,2х4 + 8

х5 = –2,2х3 – 0,8x4 + 37

q = 3,8x3 + 0,2х4 – 33

В выражении для функции q оба неизвестных входят со знаком «+». Поэтому можно утверждать, что найден оптимальный план: х3 = х4 = 0. Подставив эти значения в последнюю систему ограничений, получим и остальные неизвестные:

х1 = 17; х2 = 8; х5 = 37;

Оптимальное значение функции q = – 33, следовательно

f(x) = 33 млрд.руб.

Ответ: f(x) = 33 млрд.руб.

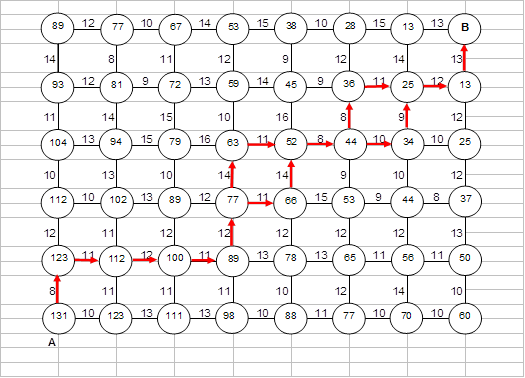
Задача №4

Метод динамического программирования для выбора оптимального профиля пути.

Задание:

Требуется найти оптимальную трассу участка железнодорожного пути между пунктами А и В, из которых второй лежит к северо-востоку от первого. Местность, по которой пройдет магистраль, является пересеченной и включает лесистые зоны, холмы, болота, реку. Поэтому стоимость строительства равных по длине участков пути может быть различной. Требуется так провести дорогу из А в В, чтобы суммарные затраты на сооружение участка были минимальны.

План прокладки пути разобьем на ряд возможных шагов, на каждом из которых стоимость строительства известна. Каждый шаг строительства является прокладкой пути между двумя рядом расположенными узлами. Все узлы пронумерованы, и в соответствии с номером варианта дана стоимость сооружения элемента пути между узлами.

Исходные данные – (вариант 67).

Решение:

Задачу решаем методом динамического программирования, последовательно двигаясь от конца трассы к ее началу, при этом на каждом шаге процесса выбирая то направление трассы, которое дает меньшую стоимость ее строительства от рассматриваемого пункта до пункта В (рис. 2).

Рис. 2

Ответ: Минимальные затраты на сооружение участка А – В составят W = 131 ден.ед.

Задача №5

Задача оптимального распределения ресурсов.

Задание (вариант 67):

Предприятие имеет свободных К млрд. руб. средств, которые оно может вложить в пять различных производственных программ. При этом прибыль от каждой из программ зависит от объема инвестиций. Эти зависимости fi известны и имеют следующий вид:

f(х) = bx – ax2

и конкретно:

f1(х1) = 0,18x1 – 0,05x12;

f2(х2) = 0,16x2 – 0,04x22;

f3(х3) = 0,14x3 – 0,02x32;

f4(х4) = 0,12x4 – 0,02x42;

f5(х5) = 0,1x5 – 0,01x52 млрд.руб.

где х1, х2, х3, х4, х5 – инвестиции в программы, млрд.руб. Их общий объем равен К = 8,5 млрд.руб.

Требуется найти неотрицательные объемы инвестиций х1, х2, х3, х4, х5 соответствующие наибольшей общей прибыли

П = f1(х1) + f2(х2) + f3(х3) + f4(х4) + f5(х5).

Решение:

Возможны следующие варианты:

1)         Все средства передаются первой программе;

2)         Средства распределяются между первой и второй программами;

3)         Средства распределяются между первой, второй и третьей программами;

4)         Средства распределяются между первой, второй, третьей и четвертой программами;

5)         Средства распределяются между первой, второй, третьей, четвертой и пятой программами.

Рассмотрим все 5 вариантов.

1)         К1 = х1 = 8,5

П1 = f1(х1) = 0,18 8,5 – 0,05 8,52 = – 2,08 млрд.руб. < 0, следов–но убыток.

2)         К2 = х1 + х2

П2 = f1(х1) + f2(х2)

0,18 – 2 0,05х1 = 0,16 – 2 0,04х2

х1 + х2 = 8,5

0,1х1 – 0,08х2 = 0,02

х1 = 8,5 – х2

0,1 (8,5 – х2) – 0,08х2 = 0,02

0,85 – 0,1х2 – 0,08х2 = 0,02

0,85 – 0,18х2 = 0,02

0,18х2 = 0,83

х2 = 4,61

х1 = 8,5 – 4,61 = 3,89

П2 = 0,18 · 3,89 – 0,05 3,892 + 0,16 4,61 – 0,04 4,612 = 0,7 – 0,757 + 0,738 – 0,85 = – 0,169 млрд.руб. < 0, следов–но убыток.

3)         К3 = х1 + х2 + х3

П3 = f1(х1) + f2(х2) + f3(х3)

0,18 – 0,1х1 = 0,16 – 0,08х2

0,16 – 0,08х2 = 0,14 – 2 · 0,02х3

х1 + х2 + х3 = 8,5

 0,18 – 0,1х1 = 0,16 – 0,08х2

0,16 – 0,08х2 = 0,14 – 0,04х3

х1 + х2 + х3 = 8,5

0,1х1 – 0,08х2 = 0,18 – 0,16 · 50

0,08х2 – 0,04х3 = 0,16 – 0,14

х1 + х2 + х3 = 8,5

5х1 – 4х2 = 1 (1)

4х2 – 2х3 = 1 (2)

х1 + х2 + х3 = 8,5 (3)

Из 2 – го ур – ия: х3 = 2х2 – 0,5

5х1 – 4х2 = 1

х1 + х2 + 2х2 – 0,5 = 8,5

5х1 – 4х2 = 1 (1)

х1 + 3х2 = 9 (2)

Из 2 – го ур – ия: х1 = 9 – 3х2

5 (9 – 3х2) – 4х2 = 1

45 – 15х2 – 4х2 = 1

19х2 = 44

х1 = 9 – 3 · 2,316 = 2,052

х3 = 2 · 2,316 – 0,5 = 4,132

П3 = 0,18 · 2,052 – 0,05 · 2,0522 + 0,16 · 2,316 – 0,04 · 2,3162 + 0,14 · 4,132 – 0,02 · 4,1322 = 0,369 – 0,21 + 0,37 – 0,215 + 0,578 – 0,34 = 0,552 млрд.руб.

4)         К4 = х1 + х2 + х3 + х4

П4 = f1(х1) + f2(х2) + f3(х3) + f4(х4)

0,18 – 0,1х1 = 0,16 – 0,08х2

0,16 – 0,08х2 = 0,14 – 0,04х3

0,14 – 0,04х3 = 0,12 – 0,04х4

х1 + х2 + х3 + х4 = 8,5

0,1х1 – 0,08х2 = 0,18 – 0,16

0,08х2 – 0,04х3 = 0,16 – 0,14 · 50

0,04х3 – 0,04х4 = 0,14 – 0,12

х1 + х2 + х3 + х4 = 8,5

5х1 – 4х2 = 1 (1)

4х2 – 2х3 = 1 (2)

2х3 – 2х4 = 1 (3)

х1 + х2 + х3 +х4 = 8,5 (4)

Из 3 – го ур – ия: х4 = х3 – 0,5

5х1 – 4х2 = 1

4х2 – 2х3 = 1

х1 + х2 + х3 + х3 – 0,5 = 8,5

5х1 – 4х2 = 1 (1)

4х2 – 2х3 = 1 (2)

х1 + х2 + 2х3 = 9 (3)

Из 2 – го ур – ия: х3 = 2х2 – 1

5х1 – 4х2 = 1

х1 + х2 + 2 (2х2 – 1) = 9

5х1 – 4х2 = 1

х1 + х2 + 4х2 – 2 = 9

5х1 – 4х2 = 1 (1)

х1 + 5х2 = 11 (2)

Из 2 – го ур – ия: х1 = 11 – 5х2

5 (11 – 5х2) – 4х2 = 1

55 – 25х2 – 4х2 =1

29х2 = 54

х2 = 1,862

х1 = 11 – 5 1,862 = 1,69

х3 = 2 · 1,862 – 1 = 2,724

х4 = 2,724 – 0,5 = 2,224

П4 = 0,18 1,69 – 0,05 1,692 + 0,16 1,862 – 0,04 1,8622 + 0,14 2,724 – 0,02·2,7242 + 0,12 2,224 – 0,02 2,2242 = 0,3 – 0,143 + 0,298 – 0,139 + 0,381 – 0,148 + 0,267 – 0,1 = 0,716 млрд.руб.

5)         К5 = х1 + х2 + х3 + х4 +х5

П5 = f1(х1) + f2(х2) + f3(х3) + f4(х4) + f5(х5)

0,18 – 0,1х1 = 0,16 – 0,08х2

0,16 – 0,08х2 = 0,14 – 0,04х3

0,14 – 0,04х3 = 0,12 – 0,04х4

0,12 – 0,04х4 = 0,1 – 0,02х5

х1 + х2 + х3 + х4 + х5 = 8,5

0,1х1 – 0,08х2 = 0,18 – 0,16

0,08х2 – 0,04х3 = 0,16 – 0,14

0,04х3 – 0,04х4 = 0,14 – 0,12

0,04х4 – 0,02х5 = 0,12 – 0,1

х1 + х2 + х3 + х4 + х5 = 8,5

0,1х1 – 0,08х2 = 0,02

0,08х2 – 0,04х3 = 0,02 50

0,04х3 – 0,04х4 = 0,02

0,04х4 – 0,02х5 = 0,02

х1 + х2 + х3 + х4 + х5 = 8,5

5х1 – 4х2 = 1 (1)

4х2 – 2х3 = 1 (2)

2х3 – 2х4 = 1 (3)

2х4 – х5 = 1 (4)

х1 + х2 + х3 +х4 + х5 = 8,5 (5)

Из 4 – го ур – ия: х5 = 2х4 – 1

5х1 – 4х2 = 1

4х2 – 2х3 = 1

2х3 – 2х4 = 1

х1 + х2 + х3 +х4 + 2х4 – 1 = 8,5

5х1 – 4х2 = 1 (1)

4х2 – 2х3 = 1 (2)

2х3 – 2х4 = 1 (3)

х1 + х2 + х3 + 3х4 = 9,5 (4)

Из 3 – го ур – ия: х4 = х3 – 0,5

5х1 – 4х2 = 1

4х2 – 2х3 = 1

х1 + х2 + х3 + 3 (х3 – 0,5) = 9,5

5х1 – 4х2 = 1

4х2 – 2х3 = 1

х1 + х2 + 4х3 – 1,5 = 9,5

5х1 – 4х2 = 1 (1)

4х2 – 2х3 = 1 (2)

х1 + х2 + 4х3 = 11 (3)

Из 2 – го ур – ия: х3 = 2х2 – 0,5

5х1 – 4х2 = 1

х1 + х2 + 4 (2х2 – 0,5) = 11

5х1 – 4х2 = 1

х1 + х2 + 8х2 – 2 = 11

5х1 – 4х2 = 1 (1)

х1 + 9х2 = 13 (2)

Из 2 – го ур – ия: х1 = 13 – 9х2

5 (13 – 9х2) – 4х2 = 1

65 – 45х2 – 4х2 = 1

49х2 = 64

х2 = 1,306

х1 = 13 – 9 1,306 = 1,246

х3 = 2 1,306 – 0,5 = 2,112

х4 = 2,112 – 0,5 = 1,612

х5 = 2 · 1,612 – 1 = 2,224

П5 = 0,18 1,246 – 0,05 1,2462 + 0,16 1,306 – 0,04 1,3062 + 0,14 2,112 – 0,02 2,1122 + 0,12 1,612 – 0,02 1,6122 + 0,1 2,224 – 0,01 2,2242 = 0,224 – 0,078 + 0,209 – 0,068 + 0,296 – 0,089 + 0,193 – 0,052 + 0,222 – 0,049 = 0,808 млрд.руб.

Ответ: Максимальное значение прибыли П5 = 0,808 млрд. руб.

Распределение инвестиций: х1 = 1,246 млрд. руб.

х2 = 1,306 млрд. руб.

х3 = 2,112 млрд. руб.

х4 = 1,612 млрд. руб.

х5 = 2,224 млрд. руб.

Задача №6

Метод экспертных оценок для отбора кандидата из кадрового резерва на должность руководителя.

Задание:

Требуется методом экспертного ранжирования из группы кадрового, включающего в себя семь кандидатов, отобрать наиболее достойного, по мнению коллектива, из 10 экспертов.

После коллективного ранжирования экспертами степени подготовленности и личностных свойств всех представителей группы кадрового резерва и выбора лучшего из них определить степень согласованности мнений группы экспертов.

Исходные данные (вариант 67):

Каждый Эj эксперт оценивает степень подготовленности каждого члена группы кадрового резерва, сопоставив ему целое число – его ранг kij, т.е. номер члена группы в порядке убывания оценки степени подготовленности. Первый ранг имеет тот, кто, по мнению эксперта, подготовлен лучше других, второй – менее подготовлен, но лучший из оставшихся.

Принято, что эксперты отличаются уровнем компетентности, которую можно оценить вероятностью получения экспертом достоверной оценки. Тогда каждый эксперт получает весовой коэффициент, значение которого лежит в пределах 0 < аj ≤ 1 для Э – го эксперта.

Решение:

Для решения задачи составим матрицу мнений экспертов в виде таблицы 1.

В таблице 1 по каждому Эj столбцу хi числу из группы резерва присваивается kij ранг – целое число от 1 до n.

Получаем матрицу мнений экспертов размерностью N·n, в которой сумма элементов любого столбца равна

Наиболее подготовленного кандидата из группы на основе коллективной оценки выбирают после расчета среднего ранга для каждого из кандидатов:

,

На первом месте будет кандидат, имеющий минимальный ранг, что будет соответствовать усредненному мнению коллектива из N экспертов.

Если мнения экспертов сильно расходятся, то необходимо ввести процент достоверности, т.е. согласованности экспертов. Согласованность экспертов определяется степенью рассеянности средних рангов .

Степень рассеяния определяется с помощью дисперсии средних рангов:

,

;

М(k) – математическое ожидание среднего ранга.

В таблице для краткости обозначений принято:

Таблица 1 - Расчет коэффициента согласованности

При полном совпадении мнений экспертов дисперсия имеет максимальное значение:

Критерий согласованности экспертов представляется в виде отношения:

,

Ответ: Выбран кандидат №5, имеющий минимальный ранг.

Мнение экспертов согласовано не очень хорошо (лишь на 30%).

Задача №7

Метод экстраполяции динамического ряда.

Задание:

Установить параметры линейной однофакторной модели расчета потребности в трудовых ресурсах, которые потребуются при росте использования оборудования за установленный период времени до 90% его мощности.

Исходные данные (вариант 7):

Временной ряд роста численности обслуживающего персонала установленного оборудования:

Решение:

Экстраполяция динамического ряда производится по уравнению прямой:

y = a + bt,

где y – необходимое количество рабочих;

t – порядковый номер динамического ряда;

a, b – параметры уравнения.

Задача состоит в определении уровня динамического ряда за пределами взятого базисного периода через определение значений параметров уравнения (a, b). Базисный период принимается по исходным данным, tбаз = 15.

Параметры модели определяются из соотношений:

; ;

;

,

где N – число мест базисного периода, N = 15.

Таблица 1 - Характеристики для расчета параметров линейной модели прогноза численности трудовых ресурсов

;

а = 21,4 – 2,464 8 = 1,688

Тогда

y = 1,688 + 2,464 t

Для N + 1 года yN+1 = 41,112.

Ответ: y = 1,688 + 2,464 t

Список использованной литературы

1.      Экономико-математическое моделирование. Учеб. для ВУЗов / Под ред. А.Д. Дрогобыцкого. – М.: Экзамен, 2004.

2.      Карпелович Ф.И., Садовский Л.Е. Элементы линейной алгебры и линейного программирования. – М.: Физматгиз, 1963.

3.      Нестеров Е.П. Транспортные задачи линейного программирования. – М.: Транспорт, 1971.
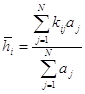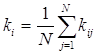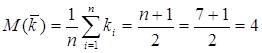
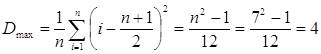
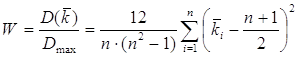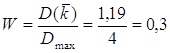
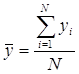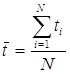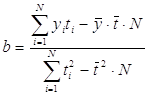