|
Рефератыкосмонавтике административному праву хозяйственному праву устройствам экологическому праву криминалогия гражданский и землепользование обществознание |
Контрольная работа: Классификации гиперболических дифференциальных уравнений в частных производныхКонтрольная работа: Классификации гиперболических дифференциальных уравнений в частных производныхСодержание Введение 1. Гиперболические уравнения как подкласс дифференциальных уравнений в частных производных. Классификация уравнений в частных производных 2. Классификация уравнений гиперболического типа в контексте классификации уравнений математической физики 2.1 Волновое уравнение 2.2 Уравнение теплопроводности 2.3 Интегро-дифференциальные уравнения 3. Применение различных методов решения в зависимости от видов гиперболических уравнений3.1 Явная разностная схема3.2 Неявная разностная схема Заключение Список литературы Настоящая курсовая работа посвящена классификации гиперболических дифференциальных уравнений в частных производных. Актуальность тематики исследования обусловлена широким кругом практических приложений гиперболических уравнений. Целью настоящей курсовой работы является приведение классификации гиперболических дифференциальных уравнений в частных производных. Задачами работы являются: 1. Рассмотреть классификацию гиперболических уравнений в рамках общей классификации уравнений математической физики. 2. Привести собственно классификацию гиперболических дифференциальных уравнений в частных производных. 3. В связи с приведенной классификацией гиперболических дифференциальных уравнений в частных производных описать применение методов решения уравнений. Изучением дифференциальных уравнений в частных производных занимается математическая физика. Основы теории этих уравнений впервые были изложены в знаменитом «Интегральном исчислении» Л. Эйлера. Классические уравнения математической физики являются линейными. Особенность линейных уравнений состоит в том, что если U и V – два решения, то функция aU + bV при любых постоянных a и b снова является решением. Это обстоятельство позволяет построить общее решение линейного дифференциального уравнения из фиксированного набора его элементарных решений и упрощает теорию этих уравнений. Современная общая теория дифференциальных уравнений занимается главным образом линейными уравнениями и специальными классами нелинейных уравнений. Основным методом решения нелинейных дифференциальных уравнений в частных производных выступает численное интегрирование. Круг вопросов математической физики тесно связан с изучением различных физических процессов. Сюда относятся явления, изучаемые в гидродинамике, теории упругости, электродинамике и т.д. Возникающие при этом математические задачи содержат много общих элементов и составляют предмет математической физики. Постановка задач математической физики, будучи тесно связанной с изучением физических проблем, имеет свои специфические черты. Так, например, начальная и конечная стадии процесса носят качественно различный характер и требуют применения различных математических методов. 1. Гиперболические уравнения как подкласс дифференциальных уравнений в частных производных. Классификация уравнений в частных производныхДифференциальные уравнения в частных производных представляют собой одну из наиболее сложных и одновременно интересных задач вычислительной математики. Эти уравнения характеризуются тем, что для их решения не существует единого универсального алгоритма, и большинство задач требует своего собственного особого подхода. Уравнениями в частных производных описывается множество разнообразных физических явлений, и с их помощью можно с успехом моделировать самые сложные явления и процессы (диффузия, гидродинамика, квантовая механика, экология и т. д.). Дифференциальные уравнения в частных производных требуют нахождения функции не одной, как для ОДУ, а нескольких переменных, например, f (х,у) или f(x,t). Постановка задач включает в себя само уравнение (или систему уравнений), содержащее производные неизвестной функции по различным переменным (частные производные), а также определенное количество краевых условий на границах расчетной области. Несмотря на то, что Mathcad обладает довольно ограниченными возможностями по отношению к уравнениям в частных производных, в нем имеется несколько встроенных функций. Решать уравнения в частных производных можно и путем непосредственного программирования пользовательских алгоритмов. Постановка задач для уравнений в частных производных включает определение самого уравнения (или системы нескольких уравнений), а также необходимого количества краевых условий (число и характер задания которых определяются спецификой уравнения). По своему названию уравнения должны содержать частные производные неизвестной функции и (или нескольких функций, если уравнений несколько) по различным аргументам, например, пространственной переменной х и времени t. Соответственно, для решения задачи требуется вычислить функцию нескольких переменных, например, u(x,t) в некоторой области определения аргументов 0<x<L и 0<t<T. Граничные условия определяются как заданные временные зависимости функции и, или производных этой функции, на границах расчетной области 0 и L, а начальные — как заданная и (х, 0). Сами уравнения в частных производных (несколько условно) можно разделить на три основных типа: · параболические — содержащие первую производную по одной переменной и вторую — по другой, причем все эти производные входят в уравнение с одинаковым знаком; · гиперболические— содержащие первую производную по одной переменной и вторую — по другой, входящие в уравнение с разными знаками; · эллиптические — содержащие только вторые производные, причем одного знака. Некоторые более сложные уравнения нельзя однозначно подогнать под приведенную классификацию, тогда говорят о гибридных типах уравнений. Будем использовать в качестве примера очень наглядное и имеющее различные, от очевидных до самых неожиданных, решения уравнение теплопроводности. Двумерное динамическое уравнение Рассмотрим следующее параболическое уравнение в частных производных, зависящее от трех переменных — двух пространственных х и у, а также от времени t:
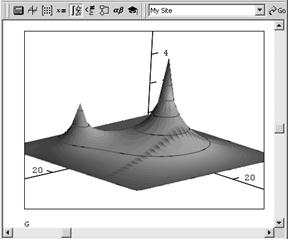
Выражение в скобках в правой части уравнения (сумму вторых пространственных производных функции и часто, ради краткости, обозначают при помощи оператора Лапласа: Δu). Это уравнение называется двумерным уравнением теплопроводности или, по-другому, уравнением диффузии тепла. Оно описывает динамику распределения температуры u(x,y,t) на плоской поверхности (например, на металлической пластине) в зависимости от времени (рис. 1). Физический смысл коэффициента о, который, вообще говоря, может быть функцией как координат, так и самой температуры заключается в задания скорости перетекания тепла от более нагретых областей в менее нагретые. Функция φ(x,y,t,u) описывает приток тепла извне, т. е. источники тепла, которые также могут зависеть как от пространственных координат (что задает локализацию источников), так и от времени и от температуры и.
Рис. 1. Физическая модель, описываемая двумерным уравнением теплопроводности Для того чтобы правильно поставить краевую задачу для двумерного уравнения теплопроводности, следует определить следующие дополнительные условия: · граничные условия, т. е. динамику функции u(x,y,t) и (или) ее производных на границах расчетной области; · начальное условие, т. е. функцию u(х, у, t). Если рассматривается не одно уравнение в частных производных, а система уравнений, то соответствующие начальные и граничные условия должны быть поставлены для каждой из неизвестных функций. Стационарное двумерное уравнение Частный случай уравнения теплопроводности определяет стационарную, т. е. не зависящую от времени, задачу. Стационарное уравнение описывает физическую картину распределения температуры по пластине, не изменяющуюся с течением времени. Такая картина может возникнуть при условии, что стационарный источник тепла действует довольно продолжительное время, и переходные процессы, вызванные его включением, прекратились. Пример численного решения такого уравнения показан на рис. 2 в виде поверхности u(х,у).
Рис. 2. Решение стационарного двумерного уравнения теплопроводности Как несложно увидеть, если искомая функция не зависит от времени, то частная производная по времени в левой части уравнения равна нулю, и само уравнение можно переписать (переобозначив ради упрощения φ<-φ/D) следующим образом:
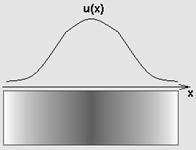
Полученное уравнение, согласно классификации предыдущего раздела, является эллиптическим. Его называют уравнением Пуассона, а для его решения в Matcad предусмотрены две встроенные функции. Если, к тому же, источники равны нулю, то уравнение (2), принимающее вид Δu=0, называют уравнением Лапласа. Одномерное динамическое уравнение Предположим, что мы рассматриваем задачу распределения тепла не по плоской поверхности, а по удлиненному телу типа металлического стержня (рис. 3). В этом случае зависимость от координаты у в общем уравнении теплопроводности пропадает, и получается одномерное уравнение:
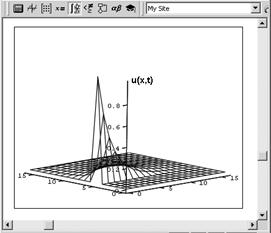
Одномерное уравнение намного проще двумерного, поскольку объем вычислений для реализации алгоритма его численного решения не так велик. Типичное решение одномерного уравнения диффузии тепла с коэффициентом диффузии о=2, нулевым источником ф=о и начальным распределением температуры в форме нагретой центральной области стержня показано (в виде графика поверхности) на рис. 3 и 4.
Рис. 3. Физическая модель одномерного уравнения теплопроводности
Рис. 4. Решение одномерного уравнения теплопроводности Линейное и нелинейное уравнения Если присмотреться к уравнению диффузии тепла внимательнее, то можно условно разделить практические случаи его использования на два типа. · Линейная задача — если коэффициент диффузии о не зависит от температуры и и, кроме того, если источник тепла ф либо также не зависит от и, либо зависит от и линейно. В этом случае неизвестная функция u (x, t) и все ее производные входят в уравнение только в первой степени (линейно). · Нелинейная задача — если уравнение имеет нелинейную зависимость от u(x,t), т. е. или коэффициент диффузии зависит от и, и (или) источник тепла нелинейно зависит от и. Решения линейных уравнений в частных производных, как правило, получаются вполне предсказуемыми, и их часто можно получить аналитически (этим проблемам посвящены соответствующие разделы науки, называемой математической физикой). В случае уравнения теплопроводности линейная задача описывает физически ожидаемое решение, выражающее остывание пластины или стержня в форме перетекания тепла от нагретого центра к холодной периферии. Нелинейные уравнения, напротив, могут демонстрировать самые неожиданные решения, причем в подавляющем большинстве практических задач их можно получить только численно, а никак не аналитически. Различные линейные и нелинейные варианты рассматриваемого уравнения теплопроводности описывают различные модели физических сред, которые характеризуются определенными зависимостями D(u) и ф(и). В частности, для металлов в большинстве случаев можно считать, что D=const, в то время как для плазмы имеется специфическая зависимость коэффициента диффузии от температуры. Обратное уравнение теплопроводности Замечательными свойствами обладает так называемое обратное уравнение диффузии тепла, которое получается путем замены в исходном (прямом) уравнении переменной t на -t. Согласно постановке задачи, обратное уравнение теплопроводности описывает реконструкцию динамики профиля температуры остывающего стержня, если известно начальное условие в виде профиля температуры в некоторый момент времени после начала остывания. Таким образом, требуется определить, как происходило остывание стержня. Мы ограничимся самым простым линейным уравнением с D=const без источников тепла:
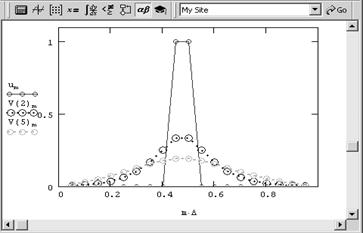
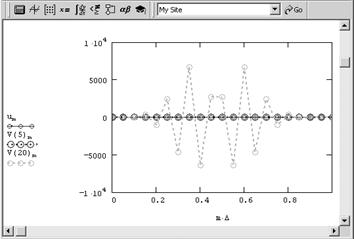
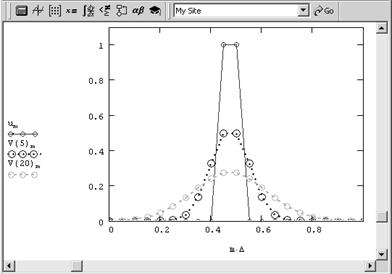
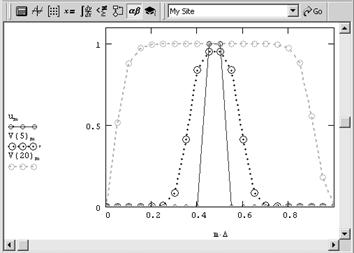
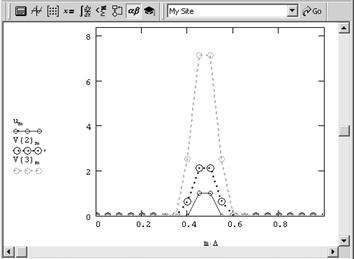
Это уравнение гиперболического типа и оно, несмотря на кажущуюся близость к рассмотренным вариантам уравнения теплопроводности, обладает замечательными свойствами. Если попробовать осуществить расчет обратного уравнения диффузии тепла по тем же самым алгоритмам, что и для обычных, то мы получим заведомо нефизичное решение. Оно показано на рис. 5 в виде профилей распределения температуры для нескольких последовательных моментов времени.
Рис. 5. Численное решение обратного уравнения теплопроводности дает совершенно нефизичную картину динамики температуры Как видно, решение выражается в появлении все более быстрых пространственных осцилляции профиля температуры для каждого нового момента времени. Очень существенно, что такое решение является не проявлением неустойчивости численного алгоритма, а определяется спецификой самой задачи. Оказывается, что обратное уравнение теплопроводности принадлежит к довольно широкому классу задач, называемых некорректными. Некорректные задачи нельзя решать стандартными методами, а для того, чтобы с ними справиться (т. е., чтобы получить осмысленное физическое решение), приходится несколько менять саму их постановку, вводя в нее дополнительную априорную информацию о строении решения. 2. Классификация уравнений гиперболического типа в контексте классификации уравнений математической физикиУравнения математической физики, дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные и т.д.), к которым приводит математический анализ физических явлений. Для теории уравнений математической физики характерна постановка задач в таком виде, как это необходимо при исследовании физического явления. Круг уравнений математической физики с расширением области применения математического анализа также неуклонно расширяется. При систематизации полученных результатов появляется необходимость включить в теорию У. м. ф. уравнения и задачи более общего вида, чем те, которые появляются при анализе конкретных явлений; однако и для таких уравнений и задач характерно то, что их свойства допускают более или менее наглядное физическое истолкование. Классификация уравнений математической физики. Значительная часть уравнений математической физики составляют линейные уравнения с частными производными 2-го порядка общего вида: где все коэффициенты aij (aij = aij), bi, с и правая часть f представляют собой заданные функции независимых переменных x1, x2,.., хп (n ³ 2), а u – искомая функция тех же аргументов. Свойства решений уравнения (5) существенно зависят от знаков корней (алгебраического относительно l) уравнения и поэтому классификация уравнений (5) проводится в соответствии с этими знаками. Если все n корней уравнения (6) имеют одинаковый знак, то говорят, что уравнение (5) принадлежит к эллиптическому типу; если один из корней имеет знак, противоположный знаку остальных n – 1 корней, – к гиперболическому типу; наконец, если уравнение (6) имеет один нулевой корень, а прочие корни одинакового знака, – к параболическому типу. Если коэффициенты aij постоянны, то уравнение (5) принадлежит к определенному типу независимо от значений аргументов; если же эти коэффициенты зависят от x1,.., хп, то и корни уравнения (6) зависят от x1,.., хп, а потому уравнение (5) может принадлежать к разным типам при различных значениях аргументов. В последнем случае (уравнение смешанного типа) изучаемая область изменения аргументов состоит из зон, в которых тип уравнения (5) сохраняется. Если корень уравнения (6), переходя от положительных значений к отрицательным, обращается в нуль, то между зонами эллиптичности и гиперболичности расположены зоны параболичности (надо отметить, что и в ряде др. отношений параболического уравнения занимают промежуточное положение между эллиптическими и гиперболическими). Для линейных уравнений с частными производными выше 2-го порядка и для систем уравнений с несколькими искомыми функциями классификация более сложна. Основные примеры уравнений математической физики. 2.1 Волновое уравнениеВолновое уравнение, дифференциальное уравнение с частными производными, описывающее процесс распространения возмущений в некоторой среде[1].
– простейшее уравнение гиперболического типа, а также соответствующие неоднородные уравнения (в правой части которых добавлены известные функции) – телеграфное уравнение и т.д. Уравнения и системы этого типа появляются при анализе различных колебаний и волновых процессов. Свойства уравнений и систем гиперболического типа во многом аналогичны свойствам приведённых простейших таких уравнений. В случае малых возмущений и однородной изотропной среды волновое уравнение имеет вид: где х, у, z — пространственные переменные, t — время, u = u (х, у, z) — искомая функция, характеризующая возмущение в точке (х, у, z) в момент t, а — скорость распространения возмущения. Волновое уравнение является одним из основных уравнений математической физики и широко используется в приложениях. Если u зависит только от двух (одной) пространственных переменных, то волновое уравнение упрощается и называется двумерным (одномерным). Волновое уравнение допускает решение в виде «расходящейся сферической волны»: u = f (t - r/a)/r, где f — произвольная функция, a Особый интерес представляет так называемое элементарное решение (элементарная волна): u = δ (t - r/a)/r (где δ — дельта-функция), дающее процесс распространения возмущения, произведённого мгновенным точечным источником (действовавшим в начале координат при t = 0). Образно говоря, элементарная волна представляет собой «бесконечный всплеск» на окружности r = at, удаляющийся от начала координат со скоростью а с постепенным уменьшением интенсивности. При помощи наложения элементарных волн можно описать процесс распространения произвольного возмущения. Малые колебания струны описываются одномерным В. у.: Ж. Д'Аламбер предложил (1747) метод решения этого В. у. в виде наложения прямой и обратной волн: u = f (x - at) + g (x + at), а Л. Эйлер (1748) установил, что функции f и g определяются заданием так называемых начальных условий. 2.2 Уравнение теплопроводностиУравнение теплопроводности – дифференциальное уравнение с частными производными параболического типа, описывающее процесс распространения теплоты в сплошной среде (газе, жидкости или твёрдом теле); основное уравнение математической теории теплопроводности. Уравнение теплопроводности выражает тепловой баланс для малого элемента объёма среды с учётом поступления теплоты от источников и тепловых потерь через поверхность элементарного объёма вследствие теплопроводности. Для изотропной неоднородной среды уравнение теплопроводности имеет вид[2]:
где r — плотность среды; cv — теплоёмкость среды при постоянном объёме; t — время; х, у, z — координаты; Т = Т (х, у, z, t) — температура, которая вычисляется при помощи Т. у.; l — коэффициент теплопроводности; F = F (x, y, z, t) — заданная плотность тепловых источников. Величины r, Cv, l зависят от координат и, вообще говоря, от температуры. Для анизотропной среды Т. у. вместо l содержит тензор теплопроводности lir, где i, k = 1, 2, 3. В случае изотропной однородной среды уравнение теплопроводности принимает вид[3]: где DT — оператор Лапласа, a2 = l/(rcv) — коэффициент температуропроводности; f = F/(rcv). В стационарном состоянии, когда температура не меняется со временем, Т. у. переходит в уравнение Пуассона DТ = f/a2 = F/l или, при отсутствии источников теплоты, в Лапласа уравнение DТ = 0. Основными задачами для уравнения теплопроводности является Коши задача и смешанная краевая задача. Первые исследования Т. у. принадлежат Ж. Фурье (1822) и С. Пуассону (1835). Важные результаты в исследовании Т. у. были получены И. Г. Петровским, А. Н. Тихоновым, С. Л. Соболевым.
– простейший пример уравнения параболического типа. Уравнения и системы параболического типа появляются обычно при анализе процессов выравнивания. Первым примером уравнений смешанного типа явилось т. н. уравнение Трикоми: Для
этого уравнения полуплоскость 2.3 Интегро-дифференциальные уравненияРяд задач математической физики приводит к интегральным уравнениям различных типов. Так, например, интегральные уравнения Вольтерра возникают в тех задачах физики, в которых существует предпочтительное направление изменения независимого переменного (например, времени, энергии и т.д.). В задаче о крутильных колебаниях возникает некоторое интегро-дифференциальное уравнение. Постановка задач и методы решения уравнений математической физики. На первом этапе развития теории У. м. ф. много усилий было затрачено на отыскание их общего решения. Уже Ж. Д'Аламбер (1747) получил общее решение волнового уравнения. Основываясь на подстановках, применявшихся Л. Эйлером (1770), П. Лаплас предложил (1773) «каскадный метод», дающий общее решение некоторых др. линейных однородных гиперболических уравнений 2-го порядка с двумя аргументами. Однако такое общее решение удалось найти в весьма редких случаях; в отличие от обыкновенных дифференциальных уравнений, для уравнений с частными производными не выделено ни одного сколько-нибудь значительного класса уравнений, для которых общее решение может быть получено в виде достаточно простой формулы. Кроме того, оказалось, что при анализе физических процессов У. м. ф. обычно появляются вместе с дополнительными условиями, характер которых коренным образом влияет на направление исследования. Широкое распространение получили методы приближённого решения краевых задач, в которых задача сводится к решению системы алгебраических (обычно линейных) уравнений. При этом за счёт увеличения числа неизвестных в системе можно достичь любой степени точности приближения. Интегро-дифференциальные уравнения, уравнения, содержащие неизвестную функцию под знаком интеграла и под знаком производной. Например, уравнение, полученное итальянским математиком В. Вольтерра в задаче о крутильных колебаниях:
Иногда интегро-дифференциальные уравнения можно свести к интегральным уравнениям или дифференциальным уравнениям. Решение интегро-дифференциальных уравнений можно искать по методу последовательных приближений[4]. Интегральные уравнения, уравнения, содержащие неизвестные функции под знаком интеграла. Многочисленные задачи физики и математической физики приводят к интегральным уравнениям различных типов. Пусть, например, требуется с помощью некоторого оптического прибора получить изображение линейного объекта А, занимающего отрезок 0 £ x £ l оси Ox, причём освещённость объекта характеризуется плотностью u(x). Изображение В представляет собой некоторый отрезок другой оси x1; последний путём подходящего выбора начала отсчёта и единицы длины также можно совместить с отрезком 0 £ x1 £ l . Если дифференциально малый участок (х, х + Dх) объекта А вызывает освещённость изображения В с плотностью K(x1, x)u(x)dx, где функция K(x1, x) определяется свойствами оптического прибора, то полная освещённость изображения будет иметь плотность
В зависимости от того, хотят ли добиться заданной освещённости v(x1) изображения или «точного» фотографического изображения [v(x) = ku(x), где постоянная k заранее не фиксируется], или, наконец, определённой разницы освещённости А и В [u(x) — v(x) = f(x)], приходят к различным интегральным уравнениям относительно функции u(x):
Вообще, линейным интегральным уравнением 1-го рода называется уравнение вида
линейным интегральным уравнением 2-го рода, или уравнением Фредгольма,— уравнение вида
[при f (x) = 0 оно называется однородным уравнением Фредгольма]; обычно рассматриваются уравнения Фредгольма с параметром l:
Во всех уравнениях функция
— так называемое ядро интегрального уравнения — известна, так же, как функция f (x) (а £ х £ b); искомой является функция u(x) (а £ х £ b). Функции K(x, y), f (x), u(x) и параметр уравнения l могут принимать как действительные, так и комплексные значения. В частном случае, когда ядро K(x, y) обращается в нуль при у > х, получается уравнение Вольтерра:
Интегральное уравнение называется особым, если хотя бы один из пределов интегрирования бесконечен или ядро K(x, y) обращается в бесконечность в одной или нескольких точках квадрата а £ х £ b, а £ y £ b или на некоторой линии. И. у. может относиться и к функциям нескольких переменных: таково, например, уравнение
Рассматриваются также нелинейные И. у., например уравнения вида
Или
Линейные интегральные уравнение 2-го рода решаются следующими методами: 1) решение u(x) получается в виде ряда по степеням l (сходящегося в некотором круге |l|<K) с коэффициентами, зависящими от х (метод Вольтерра — Неймана); 2) решение u(x), при тех значениях l, при которых оно вообще существует, выражается через некоторые целые функции от l (метод Фредгольма); 3) в случае, когда ядро симметрично, т. е. К(х, y) º К(у, x), решение u(x) выражается в виде ряда по ортогональным функциям uк(х), являющимся ненулевыми решениями соответствующего однородного уравнения
(последнее имеет отличные от нуля решения лишь при некоторых специальных значениях параметра l = lк, k = 1, 2, ..) (метод Гильберта — Шмидта); 4) в некоторых частных случаях решение сравнительно просто получается с помощью преобразования Лапласа; 5) в случае, когда
(так называемое вырожденное ядро), отыскание u(х) сводится к решению системы алгебраических уравнений. Приближённые решения можно получить, либо применив к
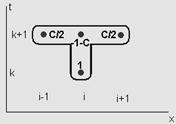
какую-либо формулу численного интегрирования, либо заменив данное ядро К(х, y) некоторым вырожденным ядром, мало отличающимся от К(х, у). К интегральным уравнениям часто сводятся краевые задачи для дифференциальных уравнений, обыкновенных и с частными производными; такое сведение имеет и теоретическую и практическую ценность[5]. 3. Применение различных методов решения в зависимости от видов гиперболических уравнений3.1 Явная разностная схемаРассмотрим сначала математические аспекты построения разностной схемы для уравнения диффузии тепла, а затем приведем примеры работы разработанного алгоритма применительно к линейному и нелинейному уравнениям. Построение разностной схемы Используем для решения уравнения теплопроводности шаблон, изображенный на рис. 6. Для дискретизации второй производной по пространственной координате необходимо использовать три последовательных узла, в то время как для разностной записи первой производной по времени достаточно двух узлов. Записывая на основании данного шаблона дискретное представление для (i, k) -го узла, получим разностное уравнение:
Приведем в разностной схеме (7) подобные слагаемые, перенеся в правую часть значения сеточной функции с индексом k (как часто говорят, с предыдущего слоя по времени), а в левую — с индексом k+i (т. е. со следующего временного слоя). Кроме этого, введем коэффициент с, который будет характеризовать отношение шагов разностной схемы по времени и пространству
Несколько забегая вперед, заметим, что значение параметра с, называемого коэффициентом Куранта, имеет большое значение для анализа устойчивости разностной схемы. С учетом этих замечаний, разностная схема (7) запишется в виде:
Рис. 6. Шаблон аппроксимации явной схемы для уравнения теплопроводности Множители для каждого из значений сеточной функции в узлах шаблона, соответствующие разностному уравнению (8), приведены рядом с каждой точкой шаблона на рис. 6. Фактически геометрия шаблона и эти множители задают построенную нами разностную схему. Несложно убедиться в том, что для получения замкнутой системы разностных алгебраических уравнений систему (8) необходимо дополнить дискретным представлением начального и граничных условий. Тогда число неизвестных будет в точности равно числу уравнений, и процесс формирования разностной схемы будет окончательно завершен. Если присмотреться к разностным уравнениям (8) повнимательнее, то можно сразу предложить несложный алгоритм реализации этой разностной схемы. Действительно, каждое неизвестное значение сеточной функции со следующего временного слоя, т. е. левая часть соотношения (8) явно выражается через три ее значения с предыдущего слоя (правая часть), которые уже известны. Таким образом, в случае уравнения теплопроводности нам очень повезло. Для расчета первого слоя по времени следует попросту подставить в (8) начальное условие (известные значения и с нулевого слоя в узлах сетки), для расчета второго слоя достаточно использовать вычисленный таким образом набор и с первого слоя и т. д. Из-за того что разностная схема сводится к такой явной подстановке, ее и называют явной, а благодаря пересчету значений с текущего слоя через ранее вычисленные слои — схемой бегущего счета. Линейное уравнение Сделанные замечания относительно реализации явной схемы для уравнения диффузии тепла сразу определяют алгоритм ее программирования в Mathcad. Для решения задачи нужно аккуратно ввести в листинг соответствующие формулы при помощи элементов программирования. Решение системы разностных уравнений (8) для модели без источников тепла, т.е. ф(x,T,t)=0 и постоянного коэффициента диффузии D=const приведено в листинге 1. В его первых трех строках заданы шаги по временной и пространственной переменным t и А, а также коэффициент диффузии о, равный единице. В следующих двух строках заданы начальные (нагретый центр области) и граничные (постоянная температура на краях) условия соответственно. Затем приводится возможное программное решение разностной схемы, причем функция пользователя v(t) задает вектор распределения искомой температуры в каждый момент времени (иными словами, на каждом слое), задаваемый целым числом t. Начальное распределение температуры вдоль расчетной области и решение для двух моментов времени показано на рис. 7 сплошной, пунктирной и штриховой линиями соответственно. Физически такое поведение вполне естественно — с течением времени тепло из более нагретой области перетекает в менее нагретую, а зона изначально высокой температуры остывает и размывается. Листинг 11. Явная схема для линейного уравнения теплопроводности
Рис. 7. Решение линейного уравнения теплопроводности (продолжение листинга 1) Нелинейное уравнение Намного более интересные решения можно получить для нелинейного уравнения теплопроводности, например, с нелинейным источником тепла ф(u)=103(u-u3). Заметим, что в листинге 1 мы предусмотрительно определили коэффициент диффузии и источник тепла в виде пользовательских функций, зависящих от аргумента и, т. е. от температуры. Если бы мы собирались моделировать явную зависимость их от координат, то следовало бы ввести в пользовательскую функцию в качестве аргумента переменную х, как это сделано для источника тепла ф. Поэтому нет ничего проще замены определения этих функций с констант D(U)=1 и ф(х,u)=о на новые функции, которые станут описывать другие модели диффузии тепла. Начнем с того, что поменяем четвертую строку листинга 1 на ф(х,и)=ю3-(и-и3), не изменяя пока постоянного значения коэффициента диффузии.
Рис. 7. Решение уравнения теплопроводности с нелинейным источником (тепловой фронт)
Рис. 8. Решение уравнения теплопроводности с нелинейным источником и коэффициентом диффузии (режим локализации горения) Читателю предлагается поэкспериментировать с этим и другими нелинейными вариантами уравнения теплопроводности. Существенно, что такие интересные результаты удается получить лишь численно, а в Mathcad только с применением элементов программирования. 3.2 Неявная разностная схемаВ отличие от явной схемы Эйлера, неявная является безусловно-устойчивой (т.е. не выдающей "разболтки" ни при каких значениях коэффициента Куранта). Однако ценой устойчивости является необходимость решения на каждом шаге по времени системы алгебраических уравнений. Построение неявной разностной схемы Чтобы построить неявную разностную схему для уравнения диффузии, используем шаблон, изображенный на рис. 9, т. е. для дискретизации пространственной производной будем брать значения сеточной функции с верхнего (неизвестного) слоя по времени. Таким образом, разностное уравнение для (i,k)-ro узла будет отличаться от уравнения для явной схемы (7) только индексами по временной координате в правой части:
Если привести подобные слагаемые, то получится система уравнений, связывающая для каждого 1-го узла три неизвестных значения сеточной функции (в самом этом узле и в соседних с ним слева и справа узлах). Множители при неизвестных значениях сеточной функции в узах шаблона показаны на рис. 9 в виде подписей, подобно тому, как это было сделано для явной схемы.
Рис. 9. Шаблон неявной схемы для уравнения теплопроводности Очень важно, что если само уравнение теплопроводности линейно, то с в левой части разностного уравнения является константой, а ф в его правой части может зависеть только от первой степени и. Поэтому система уравнений (10) для всех пространственных узлов 1=1. .м-l является линейной системой, что существенно упрощает ее решение (поскольку известно, что для линейных систем с ненулевым определителем решение существует и является единственным). Напомним, что для получения замкнутой системы линейных уравнений необходимо дополнить данный набор разностных уравнений граничными условиями, т.е. известными значениями сеточной функции для i=0 и i=M.
Рис. 9. Решение линейного уравнения теплопроводности при помощи неявной схемы на первом слое по времени (листинг 2) Листинг 2. Неявная схема для линейного уравнения теплопроводности Для реализации неявной схемы, таким образом, можно использовать комбинацию средств программирования Mathcad и встроенной функции решения системы линейных уравнений isolve. Один из возможных способов решения предложен в листинге 2. Большая часть этого листинга является вводом параметров задачи (шагов, начальных и граничных условий), и только в последней его строке определяется функция пользователя, вычисляющая сеточную функцию на каждом временном слое (при помощи встроенной функции решения системы линейных уравнений isolve). В нескольких предыдущих строках листинга (после расчета коэффициента Куранта) формируется матрица системы уравнений, которая записывается в подходящем для Mathcad виде, как это сделано в листинге 2. Как несложно убедиться, столбец правых частей разностных уравнений выражается вычисленными значениями сеточной функции с предыдущего слоя. ЗаключениеВ данной работе приведены некоторые примеры применения дифференциальных уравнений для моделирования таких реальных процессов, как колебания струны, электрические колебания в проводах, распространение тепла в стержне и пространстве, распространение температурных волн в почве, дифракция излучения на сферической частице. Во многих областях физики, математики и других естественных наук часто используются численные и эмпирические методы для решения прямых и обратных задач. Следует отметить особую роль дифференциальных уравнений при решении таких задач, поскольку не всегда удается установить функциональную зависимость между искомыми и данными переменными величинами, но зато часто удается вывести дифференциальное уравнение, позволяющее точно предсказать протекание определенного процесса при определенных условиях. Дифференциальные уравнения имеют огромное прикладное значение, являясь мощным орудием исследования многих задач естествознания и техники: они широко используются в механике, астрономии, физике, во многих задачах химии, биологии. Это объясняется тем, что весьма часто законы, которым подчиняются те или иные процессы, записываются в форме дифференциальных уравнений, а сами эти уравнения, таким образом, являются средством для количественного выражения этих законов. В заключение хотелось бы отметить особую роль дифференциальных уравнений при решении многих задач математики, физики и техники, так как часто не всегда удается установить функциональную зависимость между искомыми и данными переменными величинами, но зато удается вывести дифференциальное уравнение, позволяющее точно предсказать протекание определенного процесса при определенных условиях. Список литературы1. Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике: Учеб. пособие. М.: Наука, 1980. 686 с. 2. Бицадзе А.В. Уравнения математической физики: Учеб. М.:Наука,1982. 336 с. 3. Бицадзе А.В., Калиниченко Д.Ф. Сборник задач по уравнениям математической физики: Учеб.пособие. М.: Наука, 1977. 222 с. 4. Владимиров В. С., Уравнения математической физики, М., 1967. 5. Карслоу Г. С., Теория теплопроводности, пер. с англ., М.: Приор, 2002. 6. Канторович Л. В. и Крылов В. И., Приближённые методы высшего анализа, 5 изд., Л. — М., 1962. 7. Михайлов В.П. Дифференциальные уравнения в частных производных: Учеб.пособие. М.: Наука, 1983. 424 с. 8. Петровский И. Г., Лекции по теории интегральных уравнений, 3 изд., М., 1999. 9. Смирнов В.И. Курс высшей математики: Учеб.: В 4 т. Т.2. М.: Наука, 1981. 655 с. Т.4. М.: Наука, 1981. Ч. 2. 10. Тихонов А.Н., Самарский А.А. Уравнения математической физики: Учеб.Пособие. М.: Наука, 1977. 735 с. [1] Тихонов А. Н. и Самарский А. А., Уравнения математической физики, 3 изд., М., 1977. – с. 155. [2] Карслоу Г. С., Теория теплопроводности, пер. с англ., М.: Приор, 2002. – с. 98. [3] Владимиров В. С., Уравнения математической физики, М., 1967. – с. 155. [4] Петровский И. Г., Лекции по теории интегральных уравнений, 3 изд., М., 1999– с. 78. [5] Канторович Л. В. и Крылов В. И., Приближённые методы высшего анализа, 5 изд., Л. — М., 1962. – с. 166. |
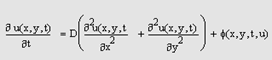 , (1)
, (1)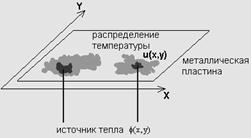
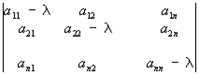 = 0, (6)
= 0, (6)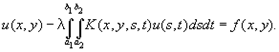
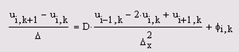 (7)
(7)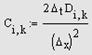

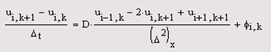 (9)
(9)