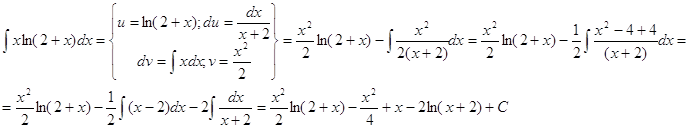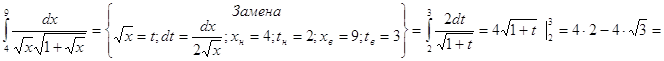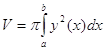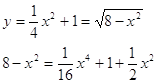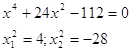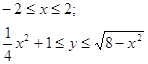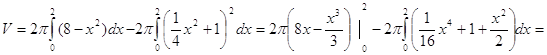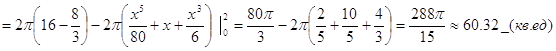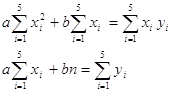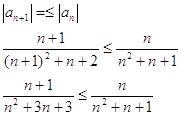Контрольная работа: Интегралы, объем тела вращения, метод наименьших квадратов

Контрольная работа: Интегралы, объем тела вращения, метод наименьших квадратов

Контрольная работа (вариант 8)

1.    Найти неопределенные интегралы:

2.                            Интегрирование по частям

 Вычислить определенные интегралы:

3.

=8-6,92=1,08

            Интегрирование по частям

4.

5. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями

. Построить чертеж.

Решение.

В декартовой системе координат построим линии и найдем точки их пересечения.

Объем тела вращения по формуле

Точки пересечения линий

(второй вариант не подходит, т.к. отрицателен)

Отсюда

Границы фигуры:

Фигура симметрична относительно оси ОУ, поэтому

Объем тела

6. Методом наименьших квадратов найти эмпирическую формулу вида y=ax+b для функции, заданной следующей таблицей:

Изобразить графически таблично заданную и соответствующую линейную функции. По эмпирической формуле вычислить значение переменной при х=4,0

Решение

Заполним таблицу

Составим для определения коэффициентов систему уравнений вида:

Получим

Решая систему методом исключения определяем:

Искомая эмпирическая формула y=28.23-4.45x

Значение переменной при x=4.0

y=28.23-4.45*4=10.43

7. Исследовать сходимость ряда.

Исследуем ряд сначала на абсолютную сходимость. Общий член ряда

В свою очередь ряд  расходится как гармонический. Значит абсолютной сходимости у исходного ряда нет. Исследуем на условную сходимость по признаку Лейбница.

1)     при

2)   

действительно для

По признаку Лейбница, исходный ряд сходится условно.