
|
Рефератыкосмонавтике административному праву хозяйственному праву устройствам экологическому праву криминалогия гражданский и землепользование обществознание |
Дипломная работа: Инверсия плоскости в комплексно сопряженных координатах3º. Две фигуры, инверсные третьей фигуре относительно одного и того же центра О, гомотетичны. □ Действительно,
пусть М – точка фигуры F,
М1 и М2 – точки, соответствующие ей в двух
инверсиях с общим центром О и коэффициентами k1 и k2. Без
ограничения общности рассуждений можно рассмотреть инверсию с центром в начале
координат. Тогда, если точки М, М1 и М2
будут иметь координаты m,
m1 и m2
соответственно, то Мы видим, что выбор степени инверсии не влияет на форму полученных фигур. Эта форма изменяется только при изменении центра инверсии. 4º. Зависимость
расстояния между образами A’ и B’ двух точек А и В от расстояния между
этими точками при инверсии с центром S и степенью k выражается в формуле □
Инверсия задается формулой 5º. Инверсия сохраняет величину угла между окружностями, а также между окружностью и прямой, между двумя прямыми, но изменяет его ориентацию на противоположную. □ Пусть заданы две
окружности (прямая и окружность, две прямые), одна из которых проходит через
точки A, B, C, а другая – через точки A, B, D. Берем точки «хорошие», то есть среди них нет
бесконечно удаленной и нулевой, так как мы будем брать инверсию с центром в
нуле. Если заданы две прямые, считаем А = В. Если A’, B’, C’,
D’ – образы этих точек при
инверсии
Согласно
геометрическому смыслу аргумента двойного отношения, он равен ориентированному
углу между окружностями (прямой и окружностью, двумя прямыми) ABC и ABD, но Следствие 1. Инверсия сохраняет двойное отношение расстояний между точками, каждая из которых не совпадает с центром инверсии и с бесконечно удаленной точкой. □ Заметим, что Для
иных наборов точек это утверждение, вообще говоря, неверно. Например, будем
предполагать, что все четыре точки различны. Если центр инверсии совпадает,
скажем, с точкой А, то, при неравенстве остальных точек бесконечно
удаленной, получаем отношение Следствие 2. Две точки и их образы при инверсии лежат на одной окружности или одной прямой. □ Не ограничивая общности
рассуждений, рассмотрим инверсию
Чтобы они лежали на прямой, нужно потребовать, чтобы точки А и В были коллинеарны с центром инверсии, причем каждая из точек даже может совпадать с центром инверсии или бесконечно удаленной точкой. ■ Следствие 3. Касающиеся окружности или касающиеся окружность и прямая переходят при инверсии в касающиеся окружности или касающиеся окружность и прямую, если только точка касания не совпадает с центром инверсии, иначе они переходят в параллельные прямые. □ Угол между касающимися окружностью и прямой или касающимися окружностями равен 0º. Если точка касания не совпадает с центром инверсии, то окружности переходят в две окружности, если центр инверсии не на одной из окружностей, в противном случае в окружность и прямую. Угол сохраняется, значит, все верно. Если же точка касания совпадает с центром инверсии, то окружность переходит в прямую, не проходящую через центр инверсии, а прямая переходит сама в себя. Угол между прямыми сохраняется и равен 0º, то есть они действительно параллельны. ■ Определение 7. Прямая называется
касательной к кривой в точке М0, если для произвольной точки
кривой М расстояние от М до прямой стремится к нулю быстрее, чем
от М до М0, когда M® М0,
то есть Определение 8. Окружность называется касательной к кривой в точке М0, если касательная к окружности в этой точке является и касательной к кривой в этой точке. Определение 9. Углом между двумя кривыми в их общей точке называется угол между касательными к этим кривым в рассматриваемой точке. Если кривые не имеют общих точек, или хотя бы одна из них не имеет касательной в общей точке, то угол между кривыми не определен. Очевидно, что угол между двумя кривыми в их общей точке также можно определить как угол между касательными окружностями (касательной окружностью и прямой) к этим кривым в рассматриваемой точке. Определение 10. Всякое преобразование, при котором сохраняются углы между кривыми, называется конформным преобразованием. Следствие 4. Инверсия есть конформное преобразование. □ Лемма.
Пусть дана окружность с центром s и
точка m0 на ней. Тогда прямая, проходящая через эту точку и
касающаяся данной окружности, будет иметь уравнение ○ Искомая касательная перпендикулярна прямой, проходящей через s и m0, и сама проходит через m0. Перенесем центр координат
в точку m0, то есть применим параллельный перенос, который будет
иметь уравнение Пусть нам даны кривые g и n, имеющие общую точку с координатой m0, и пусть каждая из них имеет касательную в этой точке – l и p соответственно. Пусть при некоторой инверсии кривые g и n перейдут в кривые g’ и n’, прямые l и p – в прямые или окружности l’ и p’. Все фигуры будут проходить через точку с координатой m’0. Угол между последними, по свойству 5, сохранится, так что остается показать, что они будут касательными к кривым g’ и n’ в точке с координатой m’0. Итак, для доказательства достаточно показать, что если дана кривая g и касательная l к ней в точке с координатой m0, то l’ будет также касательной к g’ в точке с координатой m’0. Прямая l будет касательной к кривой в точке М0
при Выполним инверсию I, пусть ее степень равна k, а центр s не в точке М0. Поместим начало
координат в s, и уравнение
инверсии будет Заметим, что по условию
выполняется Если l' –
окружность, то касательная к ней в точке М0’ будет, по лемме,
иметь уравнение Покажем, что она будет
касательной и к g’
в точке М0’, то есть Из свойства 4 имеем: Тогда По
известным неравенствам Рассматриваемый предел Но мы
брали m0 действительным числом, поэтому Если l' – прямая,
то ее уравнение совпадет с прообразом: Мы пришли к выводу, что когда центр инверсии не лежит в рассматриваемой точке, то угол между кривыми сохраняется. Если же взять центр инверсии в точке М0, то последняя отобразится в бесконечно удаленную область. Касательные l и p перейдут сами в себя и по соглашению о бесконечно удаленной области будут касаться кривых g’ и c’ в несобственной точке М’0. Можно определить угол между ними в несобственной точке как имеющийся угол между ними. ■ Следствие 5. Четное число инверсий не меняет угла между кривыми, нечетное число меняет направление угла на противоположное. 6º. Каждые две окружности или прямую и окружность можно при помощи инверсии перевести в две прямые (пересекающиеся или параллельные) или в две концентрические окружности. □ Если данные окружности или окружность и прямая касаются, то при центре инверсии в точке касания переходят в две параллельные прямые (следствие 4). Пусть даны две не касающиеся окружности действительного радиуса. Если они пересекаются, то, взяв за центр инверсии одну из точек пересечения, получим две пересекающиеся прямые (они будут пересекаться по образу второй точки пересечения). Пусть окружности не пересекаются. Если они уже концентрические, то существует две инверсии, переводящие их одна в другую. Если же они не концентрические, то в две прямые они перейти не могут, так как тогда центр инверсии должен располагаться одновременно на обеих, что невозможно. Попробуем их перевести в две концентрические окружности.
Центр инверсии лежит также на действительной оси. Действительно, центр инверсии, центр образа первой окружности и центр ее же лежат на одной прямой. Но тогда центр второй окружности лежит там же. А центры обеих окружностей принадлежат действительной оси. Пусть координаты
пересечения второй окружности с действительной осью равны а1
и а2, у первой окружности это будут точки с координатами -1
и 1. Пусть на оси дана точка О с координатой s. Тогда при инверсии с центром в точке О и
степенью k будут выполняться равенства: Полученные окружности
концентричны, если
Введем систему координат таким образом, что прямая будет мнимой осью, а центр окружности лежит на действительной оси и координата одной из точек пересечения окружности в осью равна 1, а вторая точка пересечения имеет положительную координату а. Возьмем точку на
действительной оси, не принадлежащую данной прямой и окружности, пусть ее
координата равна s. Проведем
инверсию с центром в этой точке и степенью k. Если она переведет фигуры в концентрические
окружности, то аналогично это только тогда, когда выполняется равенство Если же прямая и окружность пересекаются, то, взяв за центр инверсии одну из точек пересечения, получим две прямые. Они будут пересекаться в образе второй точки пересечения. ■ 7º. При инверсии с
центром sI и степенью k окружность с центром s радиуса r, не совпадающая с окружностью инверсии (если степень
положительна), отображается в себя тогда и только тогда, когда выполняется
равенство □ Перенесем начало
координат в центр инверсии параллельным переносом Нас интересует только
второе условие совокупности. Кстати, оно при При переходе к исходным
координатам получаем Глава 2 Применение инверсии при решении задач и доказательстве теорем 2.1. Применение инверсии при решении задач на построение. Метод инверсии дает возможность решить ряд наиболее трудных конструктивных задач элементарной геометрии. При этом его комбинация с методом координат, что фактически происходит при попытке решать задачу на комплексной плоскости, дает наиболее точные вычисления местонахождения нужных фигур, что является явным плюсом метода по сравнению с довольно неточными построениями от руки. Недостатком же этого метода является его громоздкость, связанная с необходимостью выполнить большое число довольно объемных вычислений. Но надо сказать, что для компьютера это не является трудностью, и перед пользователем встает лишь проблема перевода алгоритма решения задачи на язык программирования. Задачи на построение, решаемые методом инверсии, Александров [2] делил на три группы. Первая группа. В задачах этого рода обратные кривые играют роль геометрических мест. Центр и степень инверсии в этом случае известны. Задача 1. Даны точка К и две прямые АВ
и ВС. Провести секущую KXY так, чтобы ○ Искомые точки X и Y инверсны друг другу при инверсии с центром в точке К и степенью с2. Точка Y есть пересечение прямой ВА с кривой, обратной ВС. Это будет окружность, проходящая через центр инверсии, то есть через точку К. Найдем ее уравнение. Передвинем систему
координат таким образом, что точка К является началом координат (это
будет параллельный перенос на вектор ОК с формулой Образ прямой ВС
при инверсии будет Вычислив корни первого уравнения, подставляем их во второе. Если подойдут, это решение. Таким образом, может быть 2, 1 или 0 решений. Чтобы перевести координату Y в исходную систему координат, прибавляем к полученной координате настоящую координату К. Теперь по двум точкам – Y и К – пишем уравнение искомой
прямой: Вторая группа. В задачах этой группы инвертируется некоторая часть искомой фигуры (отрезок, точка или окружность); при этом теория инверсии, иногда в соединении с другими методами, часто укажет такую зависимость начала инверсии от данных и искомых, которая позволяет решить задачу. Начало и степень инверсии даны или должны быть целесообразно выбраны. В выборе начала, степени, числа инверсий иногда встречаются затруднения. Лучшим примером задач этого рода служит, по мнению Александрова, частный случай задачи Кастильона (Castillon), разобранный ниже. Задача 2. В данную окружность вписать треугольник так, чтобы прямые, содержащие его стороны, проходили бы соответственно через данные три точки. ○ Когда все три точки лежат на данной окружности, то решение очевидно: достаточно просто соединить эти точки и получим искомый треугольник. Решение единственно, потому что треугольник своими вершинами определяется однозначно. Если две из трех данных точек лежат на окружности и не коллинеарны с третьей, то решение также очевидно. Если третья точка лежит внутри окружности, то любая прямая, проходящая через нее пересекает окружность в двух точках. Было бы замечательно, если бы она пересекала окружность в одной из данных точек. Это можно устроить двумя способами, и решений тоже два. Если третья точка лежит вне окружности, то есть ровно один случай, при котором задача не имеет решения – если обе проведенные прямые являются касательными. То есть может быть два, одно или ни одного решения. Если только одна точка лежит на данной окружности, то решений также в лучшем случае два. Проведем прямую через точку на окружности и точку не на окружности. Получим одну сторону треугольника. Теперь проведем прямую через вторую точку не на окружности и точку пересечения полученной прямой, не совпадающей с данной, если она есть. Получим вторую сторону треугольника. Третья сторона получается автоматически. Так можно проделать с каждой из двух точек не на окружности, и решений будет два, если в каком-то или в обоих случаях не получится, что первая или вторая проведенная прямая окажется касательной. Рассмотрим случай, когда три данные точки не лежат на данной окружности. Пусть ABC – искомый треугольник, стороны АВ, ВС и СА которого проходят через три заданные точки М1, М2 и М3 с координатами m1, m2 и m3 соответственно, и вписан он в окружность w с центром S(s) и радиусом r. Поместим начало координат
в центр окружности w
при помощи параллельного переноса Заметим, что положение точки А определяет весь треугольник, поскольку прямая Am1 в пересечении с окружностью дает точку В, затем прямая Bm2 в пересечении с окружностью дает точку С. Выполним инверсию I1 с центром в точке М1
и степенью Затем осуществим инверсию
I2 с центром в точке М2 и степенью Наконец, применим
инверсию I с центром в точке S(0) и степенью Таким образом, композиция
инверсий 1) Пусть Σ – окружность или прямая, проходящая
через точку А. Обозначим Чтобы Σ перешла в прямую Σ’, необходимо, чтобы Вывод: Σ’ – прямая Û 2) Теперь аналогично
поработаем с Σ’ – прямой или окружностью, очевидно,
проходящей через А. Как мы уже выяснили, Вывод: Σ – прямая Û Теперь рассмотрим прямую AS’. По первому выводу, Угол, образованный прямой AM’ с окружностью w в результате 4 последовательных инверсий не изменится ни по величине, ни по направлению (по следствию 5). Отсюда следует, что прямые AS’ и AM’ , образующие в точке А одинаковый угол с данной окружностью, совпадут. И точка А может быть найдена как пересечение прямой S’M’ с окружностью w. В зависимости от взаимного положения этой прямой и окружности, задача может иметь два, одно или ни одного решения. Может получиться, что точки
S’ и M’ совпадут. Это происходит либо при Отсюда алгоритм решения: 1.
Переносим начало координат в точку S(s). Это параллельный перенос. Соответственно,
высчитываем новые координаты точек m1,
m2 и m3 по формуле
2. Находим координаты точек 3. Три раза заходим в процедуру решения
системы 4.
Переводим
полученные координаты в исходную систему координат: Третья группа. Всякая задача на построение дает некоторую фигуру, причем некоторые элементы этой фигуры неизвестны. Инвертируем эту фигуру. Тогда данные искомые отобразятся известным образом, и часто может случиться, что зависимость данных и искомых в отображенной фигуре гораздо проще, чем в основной фигуре. Тогда надо построить отображенную фигуру. Потом инвертировать ее обратно с тем же центром и степенью. В этом и состоит главная идея метода инверсии. Разумный выбор начала инверсии играет существенную роль: вычисления можно сильно сократить. Степень инверсии в этом случае обычно бывает произвольной. Классическим примером задач этого типа можно назвать задачу Аполлония. Задача Аполлония. Построить окружность, касающуюся трех данных окружностей. ○ Пусть даны три
окружности: Допустим, что мы уже
построили нужную окружность Таблица 1. Характер касания с искомой окружностью w.
Если у нас есть две касающиеся окружности, то выполним инверсию с центром в точке касания, эти две окружности перейдут в параллельные прямые, и задача сведется к более простой: построить окружность или прямую, составляющую с получающимися параллельными прямыми и еще одной прямой или окружностью угол в 180°. Если же нет касающихся окружностей, то применим так называемый метод расширения. Мы можем изменять наши окружности так, чтобы центры их всегда оставались постоянными, а радиусы менялись, вплоть до нулевого, и касание искомой окружности с данными сохранялось (возможно, выродившись в принадлежание точки окружности). Причем сделаем так, чтобы две из окружностей касались. Если у нас все окружности одна в другой, как матрешки, то решений, очевидно, нет. Рассмотрим противоположный случай, когда есть хотя бы две окружности не одна в другой. Для определенности, пусть это первая и вторая. Они могут быть только либо пересекающимися, либо вне друг друга. Сделаем их касающимися следующим образом. Таблица 2. Новые радиусы для окружностей одна вне другой, чтобы касались.
Таблица 3. Новые радиусы для пересекающихся окружностей, чтобы касались.
Объединим все это в новую таблицу, не учитывая вид касания. Таблица 4. Итоги.
Итак, первая и вторая окружности стали касаться. Посмотрим, может ли одна из них выродиться в точку. В первом случае х отрицателен, если окружности пересекаются, но вырождение невозможно, так как это означало бы касание изначальных окружностей внутренним образом. А третья окружность может выродиться. Во втором случае r2 точно не ноль, так как окружности не касаются внешним образом, и радиус первой явно положительное число. Но третья может выродиться. В третьем случае все аналогично. Третья же окружность может выродиться. Можно сделать вывод, что касающиеся окружности не вырождаются. Обратим внимание, что искомая окружность тоже может выродиться в общую точку всех трех окружностей – точку касания первых двух. Но третья не будет касаться их в этой точке и не выродится, иначе окружности бы изначально были касающимися. То есть, в случае получающихся трех прямых, нужно учитывать и общую точку. Вообще, задача свелась к следующей. Найти окружность, касающуюся трех данных, если две из них касаются и не вырожденные, а третья может быть вырожденной. Выполним инверсию в точке касания. Касающиеся окружности перейдут в две параллельные прямые, а оставшаяся – в окружность (точку) или прямую. Нужно найти прямую или окружность, параллельную получающимся прямым или касающуюся получающейся окружности (проходящей через точку). Причем искомая окружность или прямая не должна проходить через точку касания, иначе она при инверсии перейдет в прямую, а не окружность. Для начала ищем окружность, касающуюся двух параллельных прямых и еще одной прямой или окружности. Искомая окружность не должна проходить через А. Это вспомогательная задача 1. Затем ищем прямую, параллельную двум параллельным прямым и еще одной прямой или касающуюся заданной окружности. Искомая прямая не должна проходить через А. Но не забываем и об общей точке трех прямых – бесконечно удаленной, которая при инверсии перейдет в центр инверсии и потом, возможно, станет центром искомой окружности. Это вспомогательная задача 2. Вспомогательная задача 1. Даны две параллельные прямые и окружность, возможно вырожденная, либо прямая. Найти касающуюся всех трех фигур окружность. ○ Пусть заданы две
параллельные прямые Если задана еще одна
прямая
Если найден центр, то
радиус окружности находится как расстояние от прямой Помним, что если мы изменяли радиусы, то решением является и бесконечно удаленная точка, то есть окружность с центром в бесконечно удаленной точке и нулевым радиусом. Если
задана окружность или точка Вспомогательная задача 2. Даны две параллельные прямые и окружность, возможно вырожденная, либо прямая. Найти касающуюся всех трех фигур прямую. ○ Пусть заданы две
параллельные прямые Если дана еще окружность Если дана прямая, то если она не параллельна двум другим, то решений нет. Иначе решений бесконечно много, только нужно следить, чтобы прямые не совпали. ● Алгоритм решения задачи Аполлония может быть таким: 1. Если все окружности расположены одна
в другой, как матрешки (при одновременном выполнении условий[3]
2. Определяем две окружности не одна в
другой (для них не выполняется неравенство 3. Изменяем радиусы, делая касание;
определяем точку касания (ее координата будет равна 4. Проверяем результаты на касание. ● 2.2. Применение инверсии при доказательстве. Здесь снова используется тот факт, что зависимость данных и искомых в отображенной фигуре часто гораздо проще, чем в основной фигуре. Замечательно, если в задаче фигурирует окружность: метод дает возможность заменять фигуры, содержащие окружности, более простыми фигурами. Теорема Птолемея. Для всякого четырехугольника ABCD, вписанного в окружность, верно □ Пусть точки A, B, C, D имеют координаты a, b, c, d соответственно. Примем А за центр
инверсии, и пусть степень инверсии равна 1. При этом окружность переходит в
прямую. На этой прямой лежат образы точек B, C, D – точки B’, C’, D’,
причем порядок точек сохраняется, поскольку по след 5 сохраняется двойное отношение
точек В, В, С, D, а это есть простое отношение трех точек В, С,
D. По свойству 3 можно записать: Из-за
сохранения порядка точек верно Обратная теорема. Если для четырех неколлинеарных
точек A, B, C,
D верно □ Равенство Если это прямая, то она та же самая, и центр инверсии на ней. То есть все точки лежат на одной прямой. Противоречие условию теоремы. Значит, это была не прямая, а окружность. На ней лежат точки B, C, D. Но раз прямая переводится в окружность, то центр инверсии, то есть точка А, расположен на этой окружности. ■ Из этой теоремы следует теорема Пифагора, если четырехугольник является прямоугольником. Заключение Необходимо сразу оговориться, что работа не может претендовать на абсолютную полноту изложения данной темы. Однако цели, поставленные в начале работы, достигнуты. Выявлены и систематизированы основные определения и факты, рассмотрены основные виды задач, решаемых с помощью преобразования инверсии. Интересно было бы рассмотреть симметрию относительно вообще любой плоской кривой, но это уже тема для отдельного исследования. Дипломная работа может быть полезна студентам и учителям, ведущим факультативные занятия по данной теме. Работа легко может быть преобразована в соответствующую курсовую или дипломную работу по информатике, поскольку необходимые алгоритмы решения задач уже даны, остается только реализовать их на нужном языке программирования. Библиографический список 1. Адамар, Ж. Элементарная геометрия [Электронный ресурс]: пособие для высших педагогических учебных заведений и преподавателей средней школы. В 2 ч. Ч. 1. Планиметрия / акад. Ж. Адамар; пер. со 2 издания под ред. проф. Д. И. Перепелкина. – Изд. 3-е. – М.: Учпедгиз, 1948. – 608 с. Режим доступа: http://www.mccme.ru. 2. Александров, И. И. Сборник геометрических задач на построение [Электронный ресурс] / И. И. Александров; под ред. Н. М. Наумович. – Изд. 18-е. – М.: Учпедгиз, 1950. – 176 с. Режим доступа: http://www.mccme.ru. 3. Понарин, Я. П. Алгебра комплексных чисел в геометрических задачах [Текст]: Книга для учащихся математических классов школ, учителей и студентов педагогических вузов / Я. П. Понарин. – М.: МЦНМО, 2004. – 160 с.: ил. – ISBN 5-94057-152-2. 4. Прасолов, В. В. Задачи по планиметрии. [Электронный ресурс] / В. В. Прасолов. – На основе 4-го изд. (М.: МЦНМО, 2001) – М., 2003. – 551 с.: ил. Режим доступа: http://www.mccme.ru. 5. Яглом, И. М. Геометрические преобразования [Электронный ресурс]. В 2 ч. Ч. 2. Линейные и круговые преобразования / И. М. Яглом. – М.: Гос. изд-во технико-теорет. лит-ры, 1956. – 612 с. – (Серия «Библиотека математического кружка»; вып. 8). Режим доступа: http://www.mccme.ru. [1] Идея этого пункта рассмотрена в [5]. [2] Эти свойства сформулированы в виде фактов и теорем в источниках [1], [2], [3], [4], [5]. [3] Условия взаимного расположения окружностей даны в источнике [3] на с.88. |
Страницы: 1, 2
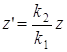 .
■
.
■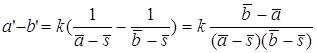 . Отсюда
. Отсюда 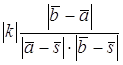 = =
= =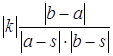 . А это и означает
. А это и означает 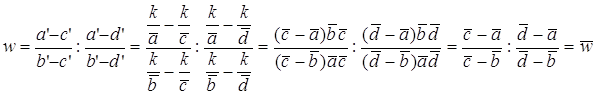 .
.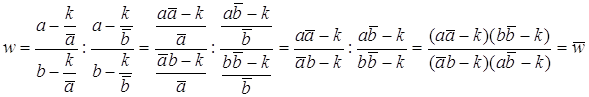 , то есть они действительно лежат или
на одной окружности, или на одной прямой.
, то есть они действительно лежат или
на одной окружности, или на одной прямой.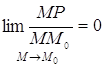 , где Р – это проекция
точки М на прямую.
, где Р – это проекция
точки М на прямую.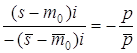 . То есть можно
взять
. То есть можно
взять 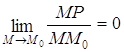 , где Р – это проекция
точки М на прямую l,
М – точка кривой g.
, где Р – это проекция
точки М на прямую l,
М – точка кривой g. 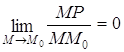 Û
Û 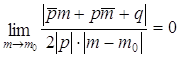 Û
Û 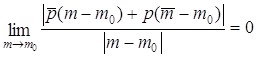 .
.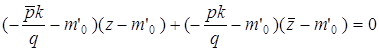 Û
Û 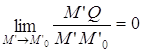 , где Q – это проекция точки М’ на
эту прямую, М’ – точка кривой g’.
, где Q – это проекция точки М’ на
эту прямую, М’ – точка кривой g’.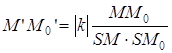 . Отсюда следует, что
. Отсюда следует, что 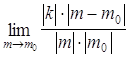 =
= 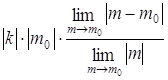 = 0. Также
= 0. Также 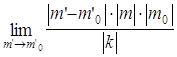 =
= 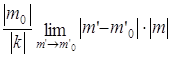 = 0.
= 0.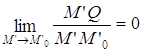 Û
Û 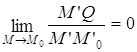 Û
Û 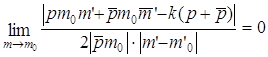 Û
Û 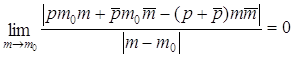 Û
Û 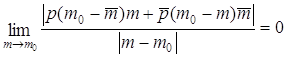 .
.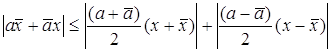 ,
, 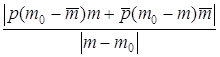 £
£ 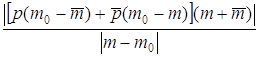 +
+ 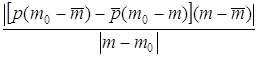 £
£ 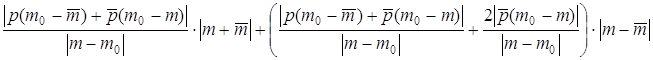 =
= 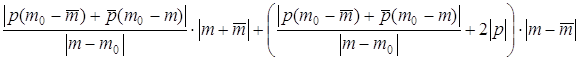 +
+ 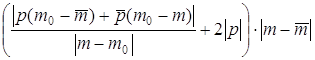 .
.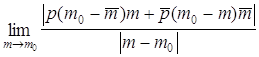 ограничен слева нулем, а
справа пределом
ограничен слева нулем, а
справа пределом 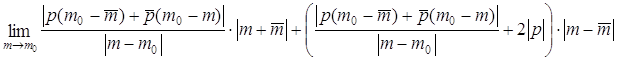 =
= 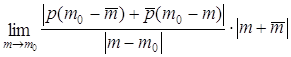 +
+ 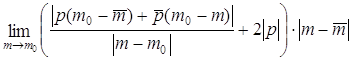 = 0 +
= 0 + 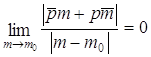 . Покажем,
что сама прямая
. Покажем,
что сама прямая 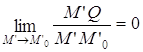 Û
Û 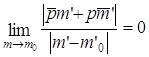 Û
Û 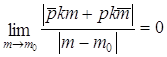 Û
Û 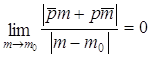 , а этот предел нам дан.
, а этот предел нам дан.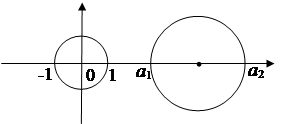 Введем систему
координат таким образом, что центры окружностей лежат на действительной оси,
причем центр одной из них совпадает с началом координат, и радиус этой
окружности равен 1.
Введем систему
координат таким образом, что центры окружностей лежат на действительной оси,
причем центр одной из них совпадает с началом координат, и радиус этой
окружности равен 1.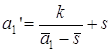 ,
, 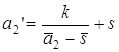 ,
, 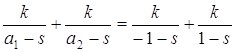 , что равносильно
, что равносильно 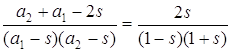 , откуда получаем
равносильное уравнение относительно s:
, откуда получаем
равносильное уравнение относительно s:  Пусть теперь даны не
касающиеся окружность и прямая. Если они не пересекаются, то, взяв центр инверсии
на прямой или окружности, получим при инверсии прямую и окружность. Не
подходит. Если возьмем центр инверсии вне прямой и окружности, то получим две
окружности. Попробуем найти инверсию, при которой они концентрические.
Пусть теперь даны не
касающиеся окружность и прямая. Если они не пересекаются, то, взяв центр инверсии
на прямой или окружности, получим при инверсии прямую и окружность. Не
подходит. Если возьмем центр инверсии вне прямой и окружности, то получим две
окружности. Попробуем найти инверсию, при которой они концентрические.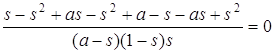 , откуда, после приведения
подобных, получаем
, откуда, после приведения
подобных, получаем 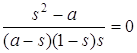 . Так как
знаменатель заведомо не равен нулю, поскольку мы так брали s, то получаем
. Так как
знаменатель заведомо не равен нулю, поскольку мы так брали s, то получаем 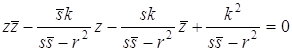 . Это
будет та же самая окружность при условии, что
. Это
будет та же самая окружность при условии, что 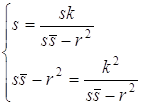 Û
Û 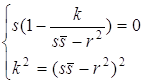 Û
Û 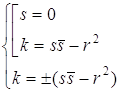 Û
Û 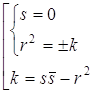 Û
Û 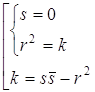 .
.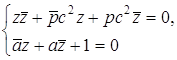 преобразовав которую,
получаем систему
преобразовав которую,
получаем систему 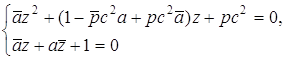
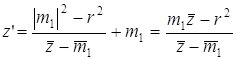 . При этом окружность w перейдет сама в себя по свойству 7:
. При этом окружность w перейдет сама в себя по свойству 7: 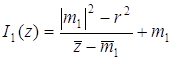 ,
, 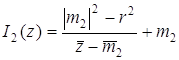 ,
, 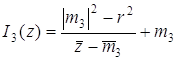 . Если координаты совпали,
то получился случай, который мы не рассматривали, иначе они задают прямую
. Если координаты совпали,
то получился случай, который мы не рассматривали, иначе они задают прямую 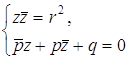 Û
Û 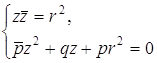 . В первый раз с
. В первый раз с 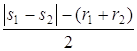
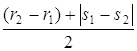
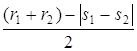
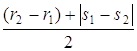
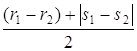
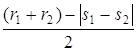
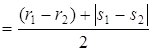
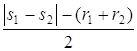
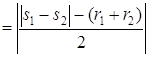
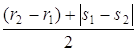
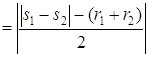
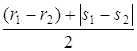
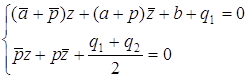 Û
Û 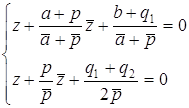 Û
Û 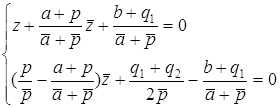 . Далее, если возможно,
находим
. Далее, если возможно,
находим 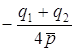 лежит на прямой
лежит на прямой 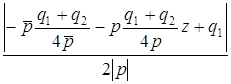 =
= 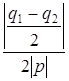 =
= 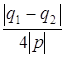 .
.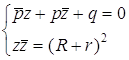 , либо систему
, либо систему 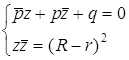 , где R – радиус искомой окружности – расстояние
между параллельными прямыми
, где R – радиус искомой окружности – расстояние
между параллельными прямыми 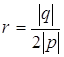 в
переобозначенных координатах. Отсюда два значения q, но нужно следить, чтобы прямые не совпали.
в
переобозначенных координатах. Отсюда два значения q, но нужно следить, чтобы прямые не совпали.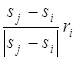 для
касающихся окружностей Si и Sj); выполняем инверсию с центром в
этой точке; решаем задачи 1 и 2, снова делаем инверсию; выводим и запоминаем
результат, если такого еще нет.
для
касающихся окружностей Si и Sj); выполняем инверсию с центром в
этой точке; решаем задачи 1 и 2, снова делаем инверсию; выводим и запоминаем
результат, если такого еще нет.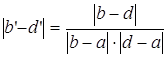 ,
, 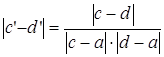 и
и 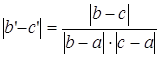 .
.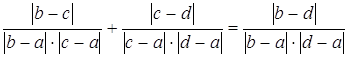 . Приведем к общему
знаменателю:
. Приведем к общему
знаменателю: 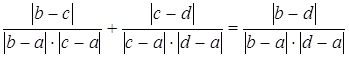 .
Получим
.
Получим