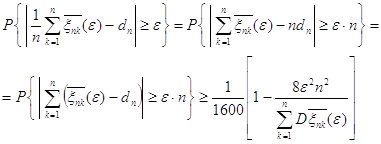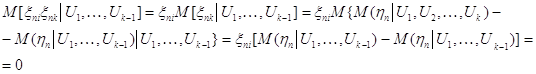|
Рефератыкосмонавтике административному праву хозяйственному праву устройствам экологическому праву криминалогия гражданский и землепользование обществознание |
Дипломная работа: Динамика развития некоторых понятий и теорем теории вероятностейОчевидно, что
Найдём число
членов до nr-n ( Что и требовалось доказать. Лемма 2. Всякая целая степень какого-либо двучлена r + s выражается числом членов, на единицу большим числа единиц в показателе степени. Доказательство. Рассмотрим
Составим ряд из степеней одночлена s (или r) 0,1,2,…, x-2, x-1, x. Число членов в этом ряду равно x+1. Т. о. всякая целая степень двучлена r + s выражается числом членов, на единицу большим числа единиц в показателе степени. Что и требовалось доказать. Лемма 3. В любой степени двучлена r + s, по крайней мере в t=r+s или nt=nr+ns, некоторый член M будет наибольшим, если числа предшествующих ему и следующих за ним членов находятся в отношении s к r или, что то же, если в этом члене показатели букв r и s находятся в отношении самих количеств r и s; более близкий к нему член с той и другой стороны больше более удалённого с той же стороны; но тот же член M имеет к более близкому меньшее отношение, чем более близкий к более удалённому при равном числе промежуточных членов. Доказательство.
Отмечается, что коэффициенты членов равноудалённых от концов равны. Число всех членов nt+1=nr+ns+1. Наибольший член будет: M= M можно записать в другом
виде, воспользовавшись следующей формулой M= Ближайший к
нему слева член равен справа – Следующий
слева – справа –
Очевидно,
что:
Что и требовалось доказать. Лемма 4. В степени
двучлена с показателем nt число n может быть взято столь
большим, чтобы отношение наибольшего члена M к двум другим L и Доказательство. M= L=
Для доказательства леммы необходимо установить, что
=
= Но эти
отношения будут бесконечно большими, когда n полагается бесконечным,
ибо тогда исчезают числа 1, 2, 3 и пр. по сравнению с n, и сами числа
Количество
сомножителей в числителе и знаменателе равно n. Вследствие чего эти
отношения будут бесконечными степенями выражений: Таким образом,
мы выяснили, что в бесконечно высокой степени двучлена отношение наибольшего
члена к другим L и
Что и требовалось доказать. Лемма 5. Отношение
суммы всех членов от L до Доказательство. M – наибольший член разложения. Пусть соседние с ним слева будут F, G, H,…; пусть соседние с L слева будут P, Q, R,…. На основании леммы 3 имеем:
Так как по
лемме 4, при n бесконечно большом, отношение Что и требовалось доказать. Главное предложение. Пусть число
благоприятных случаев относится к числу неблагоприятных точно или приближённо,
как r к s, или к числу всех
случаев, как r к r+s или r к t, это отношение
заключается в пределах Доказательство. Пусть число необходимых наблюдений будет nt. Вероятность того что все наблюдения будут благоприятны, равна
что все кроме одного–
кроме двух
А это есть
члены разложения (r+s) в степени nt (делённые на Так как
степень двучлена может быть взята столь большая, чтобы сумма членов,
заключённых между обоими пределами L и Что и требовалось доказать. Для сравнения дадим современную формулировку теоремы Бернулли. Теорема Бернулли. Если
вероятность наступления события A в последовательности независимых испытаний постоянна и равна p, то, каково бы ни было
положительное число
где Эта теорема будет доказана нами позже (после введения неравенства Чебышева). Всегда может
случиться, что, каким бы большим ни было n, в данной серии из n испытаний Бернулли считает, что из доказанной теоремы «вытекает то удивительное, по-видимому, следствие, что если бы наблюдения над всеми событиями продолжать всю вечность (причём вероятность, наконец, перешла бы в полную достоверность), то было бы замечено, что всё в мире управляется точными отношениями и постоянным законом изменения, так, что даже в вещах, в высшей степени случайных, мы принуждены были бы признать как бы некоторую необходимость и, скажу я, рок». А.А. Марков писал, что в этой работе Бернулли «впервые была опубликована и доказана знаменитая …теорема, положившая начало закону больших чисел…». Пуассон (1781–1840 гг.) в своей работе «Исследования о вероятности судебных приговоров по уголовным и гражданским делам» занимался предельными предложениями. В результате он доказал свою знаменитую теорему, которой дал название «закон больших чисел» [1]. Теорема Пуассона формулировалась следующим образом. Теорема. Если
производится n независимых испытаний, результатами которых является наступление
или не наступление события A, причём вероятность наступления события в отдельных
испытаниях неодинакова, то с вероятностью, сколь угодно близкой к единице (или,
другими словами, – к достоверности), можно утверждать, что частота Теперь эту
теорему записывают так: Если же
вероятность наступления события не будет изменяться от испытания к испытанию,
то 3.3 Неравенство Чебышева. Закон больших чисел в форме Чебышева 17.12.1866 г. Чебышев доложил Академии наук свою работу «О средних величинах», которая была опубликована в 1867 г. В «Математическом сборнике». В этой работе Чебышев доказал одно важное неравенство, которое теперь называется неравенством Чебышева. При помощи этого неравенства Чебышев получил теорему, из которой как следствия получаются теоремы Бернулли и Пуассона. В начале работы «О средних величинах» Чебышев доказывает теорему [1,6]. Теорема. Если математическое ожидание величин x, y, z,… суть a, b, c,…, а
математическое ожидание квадратов
при всяком
значении Далее Чебышев переходит к следующей теореме. Если мы
изобразим через N число величин x, y, z,…, u, полагая в доказанной сейчас теореме
то из этой теоремы получим следующую относительно средних величин. Теорема. Если математическое ожидание величин x, y, z,…, Это и есть знаменитое неравенство Чебышева, которое в современной форме записывается следующим образом:
где случайная
величина x
имеет конечную дисперсию Действительно, первую теорему Чебышева можно записать так:
Применим эту теорему к случайной величине x:
Но
Пусть Сформулируем соответствующую теорему и докажем в ней это неравенство. Теорема. Пусть имеется
случайная величина
Доказательство. 1. Пусть
величина
Изобразим
возможные значения величины Зададимся
некоторым значением Для этого
отложим от точки Для того
чтобы найти эту вероятность, нужно просуммировать вероятности всех тех значений
С другой
стороны, напишем выражение дисперсии величины
Так как все
члены суммы
Заменим под
знаком суммы выражение
Но согласно
формуле 2. В случае
когда величина
где
откуда и вытекает неравенство Чебышева для непрерывных величин. Что и требовалось доказать. Как следствие из своего неравенства Чебышев получает следующую теорему. Теорема. Если
математические ожидания величин Доказательство. Действительно,
рассмотрим случайную величину
Если
ограничены математические ожидания случайных величин и их квадратов, то
ограничены также и дисперсии, т.е. Все Применим
теперь неравенство Чебышева к
Переходя к пределу, получаем:
Что и требовалось доказать. Это и есть теорема Чебышева – закон больших чисел Чебышева. Эта теорема устанавливает, что при достаточно больших n с вероятностью, близкой к единице, можно полагать, что среднее арифметическое случайных величин как угодно мало колеблется около некоторого постоянного числа–среднего их математических ожиданий. Теоремы Пуассона и Бернулли являются частными случаями закона больших чисел Чебышева. Действительно,
пусть в n испытаниях, событие A наступает с вероятностями
где Если все
Любопытно, что Чебышев не называл доказанную теорему «законом больших чисел», хотя теорема Пуассона получается из неё как частный случай. Зная, что теорема Бернулли является частным случаем теоремы Чебышева попробуем доказать её как прямое следствие закона больших чисел Чебышева (т.е. приведём современное доказательство теоремы Бернулли [3]). Повторим современную формулировку теоремы Бернулли. Теорема. Пусть
производится n
независимых опытов. Если вероятность наступления события A в последовательности
независимых испытаний постоянна и равна p, то, каково бы ни было
положительное число
где Доказательство. Рассмотрим независимые случайные величины:
Все эти величины прерывны и имеют один и тот же закон распределения, выражаемый рядом вида:
т.к. событие A наступает с вероятностью
p и не наступает с
вероятностью q Вычислим математическое
ожидание каждой из величин
Т.к.
Отсюда и следует справедливость доказываемого неравенства:
где Что и требовалось доказать. 3.4 Закон больших чисел для зависимых случайных величин А.А. Марков под этим законом понимал закон, «в силу которого с вероятностью, сколь угодно близкой к достоверности, можно утверждать, что среднее арифметическое из нескольких величин, при достаточно большом числе этих величин, будет произвольно мало отличаться от средней арифметической их математических ожиданий». При таком понимании закона больших чисел и теорема Бернулли и теорема Пуассона и теорема Чебышева будут его различными формами. Такое понимание теперь общепринято. Чебышев
распространил закон больших чисел на независимые случайные величины с
равномерно ограниченными дисперсиями: Марков расширил условия применимости этого закона. В работе «Распространение закона больших чисел на величины, зависящие друг от друга» Марков привёл следующую теорему [1,6]. Теорема. Если
последовательность взаимно независимых случайных величин
Доказательство. Рассмотрим величину
Очевидно, что
Переходя к пределу получаем:
Что и требовалось доказать. В этой работе
Марков доказывает, что закон больших чисел применим к Марков делает
замечание: «к тому же заключению о применимости закона больших чисел не трудно
прийти и в случае, когда математическое ожидание Марков
рассматривает последовательность случайных величин, связанных в цепь. Такие
цепи зависимых величин получили название марковских цепей. В этой работе Марков
рассматривает простую цепь (простая цепь маркова – последовательность случайных
величин, каждая из которых может принимать любое число исходов, причём
вероятности исходов при В конце своей работы Марков делает вывод, что независимость величин не составляет необходимого условия для существования закона больших чисел. В настоящее время используется условие, аналогичное условию Маркова, но уже не только достаточное, но и необходимое для применимости закона больших чисел к последовательности произвольных случайных величин [4]. Теорема. Для того
чтобы для последовательности
Необходимо и
достаточно, чтобы при Доказательство. Предположим
сначала, что (2) выполнено, и покажем, что в этом случае выполнено также (1).
Обозначим через Легко проверить следующую цепочку соотношений:
Это неравенство доказывает достаточность условия теоремы. Покажем теперь, что условие (2) необходимо. Легко видеть, что
Таким
образом, Выбирая
сначала Что и требовалось доказать. 3.5 Усиление закона больших чисел. Появление необходимого и достаточного условий применимости закона больших чисел В 1923 г. А.Я. Хинчин установил закон повторного логарифма, который является своеобразным обобщением и усилением закона больших чисел[1]. Рассмотрим полученные им результаты. Согласно
теореме Бернулли, при
В 1909 г.
Борель для В 1917 г.
Кантелли распространил результат Бореля на любое В 1913 г.
Хаусдорф для случая Бернулли нашёл следующую оценку: с вероятностью единица В 1914 г.
Харди и Литтльвуд показали, что с вероятностью единица А в 1923 г. Хинчин доказал следующую теорему. Теорема. Если
вероятность появления события A в каждом из
Функция Представим
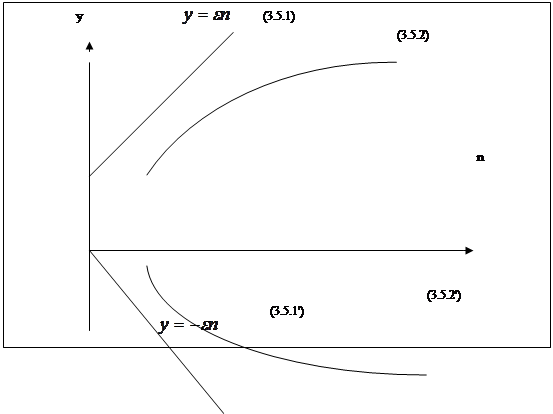
этот результат геометрически. Будем по оси абсцисс откладывать
то по теореме
Хинчина, каково бы ни было
то
Хотя Марков и расширил границы применимости закона больших чисел, однако, окончательно этот вопрос ещё не был решён. Установить необходимые и достаточные условия применимости закона больших чисел удалось только благодаря применению методов и понятий теории функций. В 1926 г. А.Н. Колмогоров установил эти условия в своей работе [5]. Определение. Случайные
величины Если
существуют все Если все Таким
образом, устойчивость ограниченной последовательности необходимо нормальна. Пусть
По
неравенству Чебышева Следовательно,
условие Маркова: Если
Следовательно,
в этом случае условие Маркова является также и необходимым для нормальной
устойчивости Если Следовательно,
в этом случае для нормальной устойчивости средних арифметических
Достаточно выполнения
следующего условия: 1. Можно
обобщить эту теорему на случай слабо коррелированных величин
достаточно
выполнения условия 2. В случае
независимых слагаемых Для каждого Положим
Теорема. Пусть
необходимы и
достаточны для устойчивости величин Доказательство. Достаточность
условий теоремы устанавливается просто. В самом деле поскольку
Для доказательства необходимости нам понадобится ряд вспомогательных предложений. Лемма 1. Пусть Доказательство. Если
существует такой номер Пусть теперь
для всех Тогда
найдётся такое
Отсюда
Что и требовалось доказать. Лемма 2. Пусть
Доказательство. Пусть
Из
неравенства
Поэтому Что и требовалось доказать. Лемма 3. Пусть
Доказательство. Обозначим Пусть теперь
одновременно
Обозначим
Предположим,
теперь, что Обозначая
На множестве Поэтому Ясно также,
что Следовательно,
и, значит, Что и требовалось доказать. Доказательство теоремы. Необходимость. Пусть
последовательность
Обозначим для
данного
Поскольку Для
достаточно больших
Далее, если
событие Но Следовательно,
Применим
лемму 1, взяв Тогда События Поскольку по
условию Положим теперь
Из Обозначим
откуда Для Тогда из
Что и требовалось доказать. 3. Дальнейшее
обобщение теоремы Чебышева получается, если предположить, что Пусть Тогда
Легко, далее,
подсчитать, что случайные величины
и,
следовательно, Итак, Таким
образом, условие Таким образом, была завершена одна из центральных проблем теории вероятностей – проблема закона больших чисел. Заключение Мы проследили динамику развития понятия вероятности; такого понятия в теории вероятностей, как математическое ожидание, а также развитие одной из центральных теорем–закона больших чисел. Можем сделать следующие выводы. Проследив динамику развития и формирования понятия вероятности можно отметить, что оно вырабатывалось сложными путями. Понятие вероятности облекалось в определения различных форм и содержаний. Вначале это понятие понимали на чисто интуитивном уровне. Позднее появились различные определения понятия вероятности. Наблюдались попытки вводить новые понятия, например «собственно вероятность», но эти попытки не увенчались успехом – это понятие не сохранилось в науке. В дальнейшем возникает необходимость в более чётком и строгом отношении к основным понятиям теории вероятностей, т.е. и к определению понятия вероятности. Этого требовало развитие статистической физики; этого требовало развитие самой теории вероятностей, в которой остро стала ощущаться неудовлетворённость классического обоснования лапласовского типа; этого требовало и развитие других наук, в которых широко применялись вероятностные понятия. Становилось всё отчётливее видно, что теория вероятностей нуждается в новом логическом обосновании – в обосновании с помощью аксиоматического метода. Многие учёные предпринимают попытки аксиоматического определения понятия вероятности. Однако успешно эта задача была решена в начале XX в. Колмогоровым. Аксиоматика Колмогорова способствовала тому, что теория вероятностей окончательно укрепилась как полноправная математическая дисциплина. Развитие понятия математического ожидания также встречало ряд трудностей. Попытки ввести понятие морального ожидания, которое бы устраняло недостатки математического ожидания – провалились. Это произошло из-за того, что понятие морального ожидания не было связано с понятием вероятности в отличие от математического ожидания. В результате понятие «математическое ожидание» заняло прочное место, по праву ему принадлежащее, в теории вероятностей. Динамику развития закона больших чисел можно сравнить с иерархической лестницей. В основании её простейшие теоремы Бернулли и Пуассона, а на вершине – критерий применимости закона больших чисел (необходимое и достаточное условия). В отличие от понятий вероятности и математического ожидания, закон больших чисел не сталкивался с подобными противоречиями, в своей трактовке. Усовершенствование закона больших чисел происходило плавно, без резких скачков. Список источников 1. Майстров Л.Е. Теория вероятностей. Исторический очерк. – М.: Наука, 1967. – 320 с. 2 Майстров Л.Е. Развитие понятия вероятности. – М.: Наука, 1980. – 270 с. 3 Вентцель Е.С. Теория вероятностей. – М.: Наука. Главная редакция физ. – мат. литературы, 1969. – 576 с. 4 Гнеденко Б.В. Курс теории вероятностей. – М.: Наука. Главная редакция физ. – мат. литературы, 1969. – 400 с. 5 Колмогоров А.Н. Основные понятия теории вероятностей. – М.: Наука. Главная редакция физ. – мат. литературы, 1974. – 120 с. 6 История отечественной математики. В 4 т.–К.: Навукова думка, 1967. – Т.2. 7 Гливенко В.И. Курс теории вероятностей. – М.: Гостехиздат, 1939. 8 Чебышев П.Л. Полное собрание сочинений – М.–Л.: 1948.–Т.3. 9 История естествознания в России. – М.: 1960.–Т.2. 10 Гнеденко Б.В., Колмогоров А.Н. Теория вероятностей. – В кн.: «Математика в СССР за 30 лет». – М. – Л.: 1948. |
Страницы: 1, 2
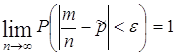
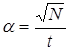 ,
разделим на N как сумму x+y+z+…,
так и пределы её
,
разделим на N как сумму x+y+z+…,
так и пределы её 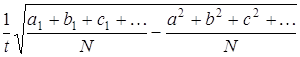 при всяком значении, будет
превосходить
при всяком значении, будет
превосходить 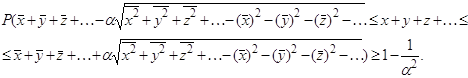
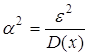 и получаем привычную
формулу для неравенства Чебышева
и получаем привычную
формулу для неравенства Чебышева 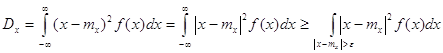 ,
,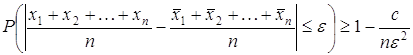 .
.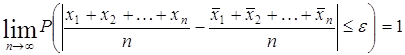 .
.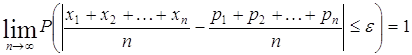 , или
, или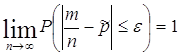 ,
, 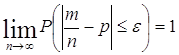 .
.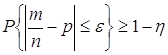 ,
, 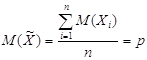 , а
, а 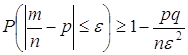 .
.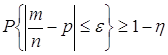 ,
, 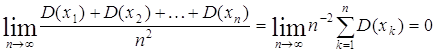 , то
, то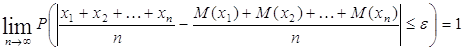 .
.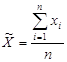 ,
, 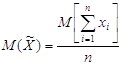 .
.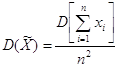 и величина
и величина 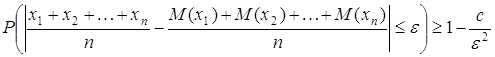 .
.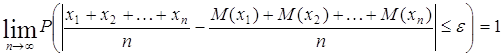 .
.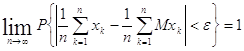 , (3.4.1)
, (3.4.1)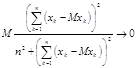 . (3.4.2)
. (3.4.2)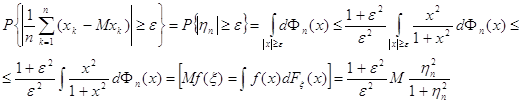
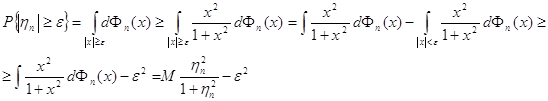
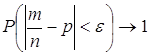
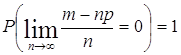 , т.е. что
, т.е. что 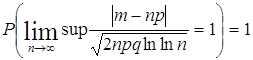 .
.
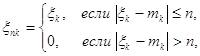
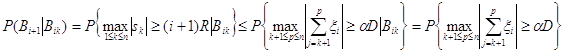
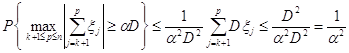 .
. 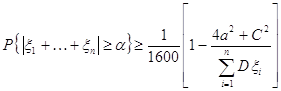 .
.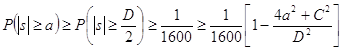 .
.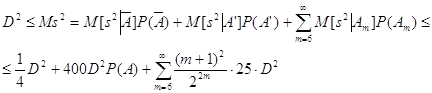
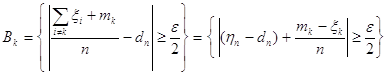 .
.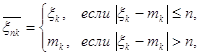
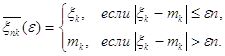
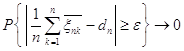 ,
, 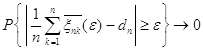 .
.